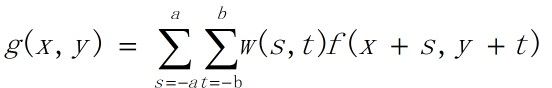对图像滤波的理解
每次看文献都会在看一些表达式的时候转不过弯,不能立马就理解作者的思想是如何用数学表达式来表达的,今天看了一篇关于滤波器的论文,突然有点灵感,特意记录下来,当然,非常狭隘。
一般图像的滤波就是利用一个滤波器对图片进行卷积。但是滤波又分为空域(图像未经过变换,像素的操作一般为加权求和,即模板卷积)和频域(图像变换到频域后与滤波器函数相乘(滤除不需要的频率成分),然后反变换得到滤波后的图像)的滤波。
以下是以空域高斯滤波为例:
目标点上的像素值通常是由其所在位置上的周围的一个小局部邻域像素的值所决定。在2D高斯滤波中的具体实现就是对周围的一定范围内的像素值分别赋以不同的高斯权重值,并在加权平均后得到当前点的最终结果。而这里的高斯权重因子是利用两个像素之间的空间距离(在图像中为2D)关系来生成。通过高斯分布的曲线可以发现,离目标像素越近的点对最终结果的贡献越大,反之则越小。其公式化的描述一般如下所述:
其中的w为基于空间距离的高斯权重;而d(x)用来对结果进行单位化,就类似于空域滤波中加权后再除以加权系数之和;积分限为无穷表示窗口无穷大,实际看自己需要可以修改;f(·)表示图像的一个像素。
以上两个公式都是用连续函数表达,采用的是数学上的积分,或者说双重积分符号来表达对像素点的加权求和。如果是采用离散的求和符号表达,则采用如下表达式:
w(s,t)即滤波模板中的加权系数,a和b为模板的大小,一般选择奇数,f(x+s,y+t)为滤波模板覆盖处的图像像素值,另外,模板卷积时需要对图像边缘进行扩展,扩展方式可以参考冈萨雷斯的图像处理书籍。
实际编程实现的时候一般也都是将连续积分号表达成离散形式,这样才能对单个像素点进行操作,相对比较直观。