字符串相关处理kmp,前缀数,后缀树,后缀数组,最长回文串,最长重复字串,最长非重复字串
字符串相关处理kmp,前缀数,后缀树,后缀数组,最长回文串,最长重复字串,最长非重复字串
1. 最长回文串
一般用后缀数组或者后缀树可以解决,
用此方法:http://blog.csdn.net/v_july_v/article/details/6897097
- 预处理后缀树,使得查询LCA的复杂度为O(1)。这步的开销是O(N),N是单词S的长度 ;
- 对单词的每一位置i(也就是从0到N-1),获取LCA(S(i), S‘(N-i-1)) 以及LCA(S(i), S’(n-i))。查找两次的原因是我们需要考虑奇数回文和偶数回文的情况。这步要考察每坨i,所以复杂度是O(N) ;(s'是s的翻转串)
- 找到最大的LCA,我们也就得到了回文的中心i以及回文的半径长度,自然也就得到了最长回文。总的复杂度O(n)。 (在前文中提到求树种两个节点的最近公共父节点也是用的lca,此题也是相类似,找到s和s'的最近父节点之后可以,则父节点到root之间的便是回文)
找出S[0 - i].reverse() 与 S[i, n]的LCA
找出S[0 - i].reverse() 与 S[i + 1, n]的LCA
从些个LCAs里面选出最大的1
1.1 是不是想到一种求s和s'最长公共子串(注意不是最长公共子序列)?
这个方法在有时候不work,
S = “abacdfgdcaba”, S’ = “abacdgfdcaba”.
The longest common substring between S and S’ is “abacd”.明显错误。
1.2
依次遍历字符串S中可能的中心点,注意,中心点可能在字符,也可能在两个字符之间
- //从中心向两端扩展
- string expandAroundCenter(string s,int c1,int c2)
- {
- int l=c1;
- int r=c2;
- int n=s.length();
- while (l>=0 && r<=n-1 && s[l]==s[r])
- {
- l--;
- r++;
- }
- return s.substr(l+1,r-l-1);
- }
- //方法3:从中心向两端扩展
- string IsPalindrome3(string str)
- {
- int n=str.length();
- if (n==0)
- {
- return "";
- }
- string longest=str.substr(0,1);
- for (int i=0;i<n-1;i++)
- {
- string p1=expandAroundCenter(str,i,i);
- if (p1.length()>longest.length())
- {
- longest=p1;
- }
- string p2=expandAroundCenter(str,i,i+1);
- if (p2.length()>longest.length())
- {
- longest=p2;
- }
- }
- return longest;
- }
1.3 动态规划(时间复杂度也是n^2)
Define P[ i, j ] ← true iff the substring Si … Sj is a palindrome, otherwise false.
P[ i, j ] ← ( P[ i+1, j-1 ] and Si = Sj )
This yields a straight forward DP solution, which we first initialize the one and two letters palindromes, and work our way up finding all three letters palindromes, and so on…
- //方法2:动态规划
- string IsPalindrome2(string str)
- {
- if (str=="")
- {
- return "";
- }
- int n=str.length();
- int maxIndex=0;
- int maxLength=1;
- bool IsPal[1000][1000]={false};
- for (int i=0;i<n;i++)
- {
- IsPal[i][i]=true;
- }
- for (int i=0;i<n-1;i++)
- {
- if (str[i]==str[i+1])
- {
- IsPal[i][i+1]=true;
- maxIndex=i;
- maxLength=2;
- }
- }
- for (int len=3;len<=n;len++)
- {
- for (int i=0;i<=n-len;i++)
- {
- int j=i+len-1;
- if (IsPal[i+1][j-1] && str[i]==str[j])
- {
- IsPal[i][j]=true;
- maxIndex=i;
- maxLength=len;
- }
- }
- }
- return str.substr(maxIndex,maxLength);
- }
1.4
但是有一种巧妙的方法,不构建后缀树在o(n)完成
转自:http://www.felix021.com/blog/read.php?2040
首先用一个非常巧妙的方式,将所有可能的奇数/偶数长度的回文子串都转换成了奇数长度:在每个字符的两边都插入一个特殊的符号。比如 abba 变成 #a#b#b#a#, aba变成 #a#b#a#。 为了进一步减少编码的复杂度,可以在字符串的开始加入另一个特殊字符,这样就不用特殊处理越界问题,比如$#a#b#a#。
下面以字符串12212321为例,经过上一步,变成了 S[] = "$#1#2#2#1#2#3#2#1#";
然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度(包括S[i]),比如S和P的对应关系:
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
(p.s. 可以看出,P[i]-1正好是原字符串中回文串的总长度)
那么怎么计算P[i]呢?该算法增加两个辅助变量(其实一个就够了,两个更清晰)id和mx,其中id表示最大回文子串中心的位置,mx则为id+P[id],也就是最大回文子串的边界。
然后可以得到一个非常神奇的结论,这个算法的关键点就在这里了:如果mx > i,那么P[i] >= MIN(P[2 * id - i], mx - i)。就是这个串卡了我非常久。实际上如果把它写得复杂一点,理解起来会简单很多:
if (mx - i > P[j])
P[i] = P[j];
else /* P[j] >= mx - i */
P[i] = mx - i; // P[i] >= mx - i,取最小值,之后再匹配更新。
当然光看代码还是不够清晰,还是借助图来理解比较容易。
当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j],见下图。
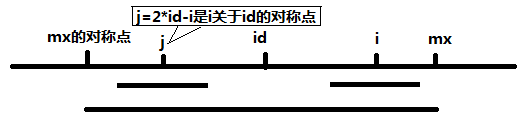
当 P[j] > mx - i 的时候,以S[j]为中心的回文子串不完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,就只能老老实实去匹配了。

对于 mx <= i 的情况,无法对 P[i]做更多的假设,只能P[i] = 1,然后再去匹配了。
于是代码如下:
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++) {
p[i] = mx > i ? min(p[2*id-i], mx-i) : 1;
while (s[i + p[i]] == s[i - p[i]]) p[i]++;
if (i + p[i] > mx) {
mx = i + p[i];
id = i;
}
}
//找出p[i]中最大的
- int Palindrome(char *str)
- {
- int len = strlen(str);
- char *Str = new char[len+len+3];
- memset(Str,0,len+len+3);//
- Str[0] = '$';
- int Len = len+len+2;
- int *scale = new int[Len];
- memset(scale,0,sizeof(int)*Len);
- int j=0;
- for (int i=1;i<Len;++i)
- {
- if(i%2==0)
- Str[i] = str[j++];
- else
- Str[i] = '#';
- }
- Str[Len] = '\0';
- int id = 0;//在i之前的回文段,这个回文段的中心点,这个回文段的右边的边界最大
- int mx = 0;//在i之前的回文段,这个回文段的右边的边界最大
- for (int i=1;i<Len;++i)
- {
- if (mx >i)//如果之前的回文边界超过i,要找到i关于回文中心点id的对称点j
- {
- int j = 2*id - i;
- int rightSpan = mx - i;
- if(scale[j]>rightSpan)
- scale[i] = rightSpan;
- else
- scale[i] = scale[j];
- }else scale[i] = 1;
- int right = i + scale[i] +1;
- int left = i - scale[i] -1;
- while ( (right<Len) && (Str[right]==Str[left]) )
- {
- ++scale[i];
- ++right;
- --left;
- }
- if (i+scale[i]>mx)
- {
- mx = scale[i];
- id = i;
- }
- }
- int maxValue = 0;
- //cout<<"Len "<<Len<<endl;
- for (int i=0;i<Len;++i)
- {
- //cout<<i<<endl;
- if(scale[i]>maxValue)
- maxValue = scale[i];
- }
- //cout<<"out"<<endl;
- delete []Str;
- delete []scale;
- return maxValue ;
- }
- 查找字符串o是否在字符串S中。
方案:用S构造后缀树,按在trie中搜索字串的方法搜索o即可。
原理:若o在S中,则o必然是S的某个后缀的前缀。
例如S: leconte,查找o: con是否在S中,则o(con)必然是S(leconte)的后缀之一conte的前缀.有了这个前提,采用trie搜索的方法就不难理解了。。 - 指定字符串T在字符串S中的重复次数。
方案:用S+’$'构造后缀树,搜索T节点下的叶节点数目即为重复次数
原理:如果T在S中重复了两次,则S应有两个后缀以T为前缀,重复次数就自然统计出来了。。 - 字符串S中的最长重复子串
方案:原理同2,具体做法就是找到最深的非叶节点。
这个深是指从root所经历过的字符个数,最深非叶节点所经历的字符串起来就是最长重复子串。
为什么要非叶节点呢?因为既然是要重复,当然叶节点个数要>=2。 (此方法应该只能找到可重叠的最长重复字串,譬如abcbcbd,可重叠最长重复字串是bcb,可以看出两个字串bcb在b上重叠了;其不重叠最长重复字串是bc和cb,用后缀树暂时想不出什么方法) - 两个字符串S1,S2的最长公共部分
方案:将S1#S2$作为字符串压入后缀树,找到最深的非叶节点,且该节点的叶节点(这里是指该节点的所有叶子节点)既有#也有$。 (譬如s1=abcd, s2 = ebce,连接组合成abcd#ebce$,

第四题可以看做是longest common substring,可以就是说要求最长公共字串必须是连续的,用后缀树或者后缀数组的时间复杂度是o(n+m)
当然还可以用动态规划实现,o(n*m):(为了避免边界检查,f[][]都是从1开始计算的,但是f[i][j],表示的是a[i-1]b[j-1])
- char a[]="acbedf";
- char b[]="ecbedfacabe";
- int f[50][50];
- memset(f,0,sizeof(f));
- int maxL=0,ai=0;
- for (int i=1;i<=sizeof(a);++i)
- {
- for(int j=1;j<=sizeof(b);++j)
- {
- if(a[i-1]==b[j-1])
- {
- f[i][j] =f[i-1][j-1] +1;
- if (f[i][j]>maxL)
- {
- maxL = f[i][j];
- ai = i-1;
- }
- }
- }
- }
- char c[50];
- memset(c,0,sizeof(c));
- strncpy(c,a+ai-maxL+1,maxL);
- cout<<maxL<<endl<<c<<endl;
以上代码主要参考:http://sagittarix.blogspot.com/2008/11/blog-post_06.html
| \ |
e |
d |
c |
e |
d |
n |
| n |
0 |
0 |
0 |
0 |
0 |
1 |
| c |
0 |
0 |
1 |
0 |
0 |
0 |
| e |
1 |
0 |
0 |
1 |
0 |
0 |
| d |
0 |
1 |
0 |
0 |
1 |
0 |
| t |
0 |
0 |
0 |
0 |
0 |
0 |
我们把两个字符串看作矩阵的x-y轴:首先遍历字符串时,把两个字符相同的位置标记成1,不相同的地方标记成0。很容易证明,如果能形成公共子序列,则最长子序列一定是从某个位置开始的对角线的长度,所以我们需要做的就是统计对角线的长度。
例如str1=”ncedt”与str2=”edcedn”生成的矩阵如左矩阵,遍历找到最长的对角线即可。
| e |
d |
c |
e |
d |
n |
|
| n |
0 |
0 |
0 |
0 |
0 |
1 |
| c |
0 |
0 |
1 |
0 |
0 |
0 |
| e |
1 |
0 |
0 |
2 |
0 |
0 |
| d |
0 |
2 |
0 |
0 |
3 |
0 |
| t |
0 |
0 |
0 |
0 |
0 |
0 |
其实这里还可以优化,即在生成表格的时候,加上对角线上比它前面的元素,这样一遍遍历就可以生成左图所示矩阵,中间记下最大值便可,省下最后一趟比较,降低时间复杂度;空间复杂度也可降低,其实只要一维的数组便可以了,因为每次更新只用到上面一行(或左边一列,看你程序怎么写了,都可以)。
这个直观上很好理解,但拆分到子问题的思想表达起来比较绕,就转一下别人的文字:
---------------------------------------------------------------------------------------------------------------------
定义f(m, n)为串Xm和Yn之间最长的子字符串的长度并且该子字符串结束于Xm 和 Yn。因为要求是连续的,所以定义f的时候多了一个要求,即字符串结束于Xm 和 Yn。
于是有f(m, 0) = f(0, m) = 0
如果xm != yn, 则f(m, n) = 0
如果xm = yn, 则f(m, n) = f(m-1, n-1) + 1
因为最长字符串不一定结束于Xm 和 Yn末尾,所以这里必须求得所有可能的f(p, q) | 0 <>最大的f(p, q)就是解。依照公式用Bottom-up DP可解。
代码就不写了,简单。但是它与其它的DP填表又有所不同,不是直接得出最大的填到表格最后一格中,而是找出格子中的最大值,其中差别,细细体会
还有一个问题是 longest common subsquence ,要求最长公共序列不一定是连续的,但是有序的,一般只能用动态规划实现,o(n*m)
算法导论讲的很透彻,这个博客也不错:http://blog.csdn.net/orbit/article/details/6717125
现在来分析一下本问题的最优子结构。首先定义问题,假设有字符串str1长度为m,字符串str2长度为n,可以把子问题描述为:求字符串str1<1..m>中从第1个到第i(i <= m)个字符组成的子串str1<1…i>和字符串str2<1..n>中从第1个到第j(j <= n)个字符组成的子串str2<1…j>的最长公共序列,子问题的最长公共序列可以描述为d[i,j] = { Z1,Z2, … Zk },其中Z1-Zk为当前子问题已经匹配到的最长公共子序列的字符。子问题定义以后,还要找出子问题的最优序列d[i,j]的递推关系。分析d[i,j]的递推关系要从str1[i]和str2[j]的关系入手,如果str1[i]和str2[j]相同,则d[i,j]就是d[i-1,j-1]的最长公共序列+1,Zk=str1[i]=str2[j];如果str1[i]和str2[j]不相同,则d[i,j]就是d[i-1,j]的最长公共序列和d[i,j-1]的最长公共序列中较大的那一个。
最后是确定d[i,j]的边界值,当字符串str1为空或字符串str2为空时,其最长公共子串应该是0,也就是说当i=0或j=0时,d[i,j]就是0。d[i,j]的完整递推关系如下:
d[i,j]表示,对于序列str1[0,i]和str2[0,j]的lcs
构建一颗后缀树的编码难度较大,一般解题应该用后缀数组:http://dongxicheng.org/structure/suffix-array/
有时间再研究下后缀数组吧。。。
