KMP算法(未完待续)
KMP算法由Knuth、Morris、Pratt三位前辈提出来的,取了这三个人的名字的头一个字母。
用途:用于处理字符串匹配,判断主串是否包含模式串。
举例:
匹配的结果:返回匹配的下标3
KMP思想:每当一趟匹配过程中出现字符比较不等时,不需回溯主串指针,而仅仅移动模式串,从而尽可能地减少比较次数。
与朴素方法的区别:
朴素方法:当匹配失败时,主串指针会回溯
Kmp算法:当匹配失败时,主串指针不会回溯
举例:使用模式串T去匹配主串S:
朴素的方法:
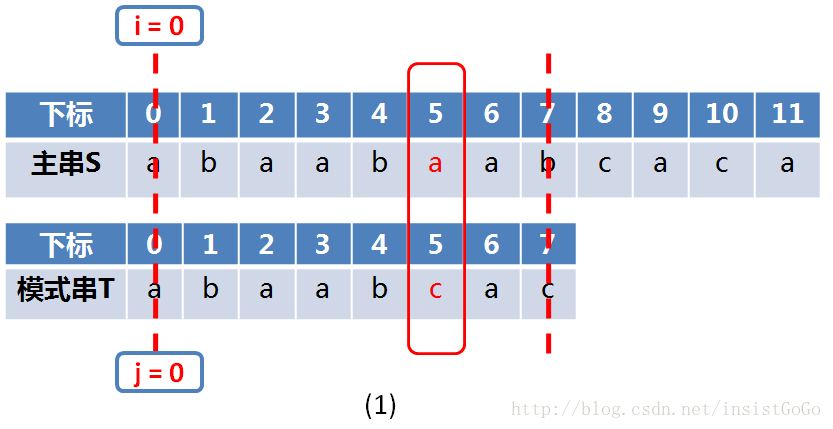
1、如图(1)所示,使用朴素方法匹配时,主串游标从i = 0开始匹配,第一趟要比较的字符区间为[0,7]。
在匹配的过程中,当主串游标 i = 5,模式串游标 j = 5 时,匹配失败。
2、如图(2)所示,匹配失败时,主串游标将从上一次匹配的起始点(i = 0)的下一位(i = 1)重新与模式串的起点(j = 0)开始匹配,即i将从i = 5退到i = 1,模式串游标j也从j = 5退到 j=0开始重新匹配,即主串和模式串都需要回溯。匹配过程一直执行到匹配成功或者主串遍历完毕为止。
时间复杂度:O(m*n),n表示主串长度,m表示模式串长度
缺点:在匹配不成功时,主串游标要回溯到上一次匹配起始点的下一位,模式串都要回到起点重新开始匹配。在这个过程中,其实做了不少重复的工作,造成时间上的浪费。
其实第二次匹配可以从(i = 5,j= 2)开始匹配。如图(3)所示。
为什么呢,这就是我们的KMP算法。
------------------------KMP算法-------------------------
KMP算法:
KMP算法和朴素算法最大的区别就是,每当匹配失败时,KMP算法不会回溯主串指针(i),而且也不一定每次都从模式串的起始位置进行匹配。
现在解释下,当第一次匹配失败时,KMP算法为什么会从图(3)这个状态开始匹配。
1、如图(4)所示,在第一次匹配失败时,主串和模式串的游标分别为(i = 5,j = 5)。
此时说明之前比较过的字符都是匹配的,即主串的[0,4]和模式串的[0,4]都是相等的。
此时可以进一步推出主串区间[3,4]和模式串区间[3,4]时匹配的,如图(5)所示。
2、如图(6)所示,对于模式串T,又因为区间[0,1]和区间[3,4]之间的字符相等。那么在下一次匹配时,模式串中区间[0,1]之间的字符就不用再与主串的区间[3,4]的字符匹配了,而直接让主串S上一次不匹配的位置(i=5)与区间[0,1]的下一个位置j=2开始匹配,这样就可以省去区间[0,1]之间的字符的比较。
3、即如图(7)所示,在第二次匹配时,主串从i=5,模式串从j=2开始匹配。
此时可以总结下,用KMP算法进行匹配时,主要的亮点是,当匹配失败时,主串游标i不动,模式串游标j尽可能远的往右移动,此时j之前的区间[0,j-1]不用比较,直接跳过去。
下面我们需要解决的问题是:当主串在第i个位置与模式串第j个位置匹配失败时,j的位置移动到哪里?
在上面的例子中,之所以模式串能在j = 2的位置比较,是因为我们事先假设知道:
(1)主串区间[0,4]和模式串区间[0,4]中的字符时相等的。
(2)模式串区间[0,1]和[3,4]中的字符时相等的。
对于(1),这两个区间的字符相等是肯定的。
原因是,我们之所以能对主串的第i个字符和模式串的第j个字符匹配,就是因为它们之前的j个字符(下标从0开始)肯定相等。
对于(2),如果不事先做一些预处理操作,是无法直接找到字符都相等的区间的。
此时我们的重点就是怎么寻找这个区间。
下面我们需要解决的问题是:当主串的第i个字符与模式串的第j个字符不匹配时,在模式串的字符区间[0,j-1]中,是否存在一个长度为t最大区间,使得模式串区间[0,t-1]和区间[j-t,j-1]中的字符相等?这里,t应该取相等区间的最大值长度。
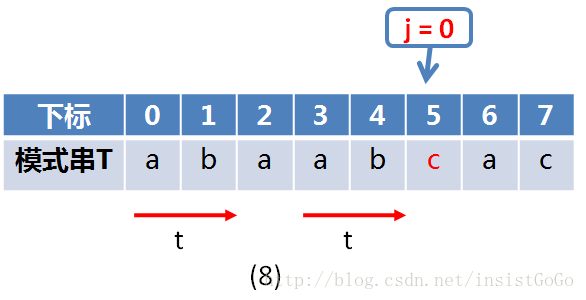
举例:如图(8)所示,在j=5时,在区间[0,4]中,存在一个最大区间长度t =2,使得模式串区间[0,1]和模式串区间[3,4]之间的字符相等。
根据我们的观察可知,对于模式串T中的第j个字符,其区间t值的求解和主串没有关系。我们可以直接在模式串中找到一个最大t值,使得区间[0,t-1] 和 区间[j - t,j-1]中的字符相等即可。
为了在主串和模式串匹配过程中,对于模式串T中的每一个字符,都能直接其t值,我们可以预处理一个数组next数组来存储这个t值。
如果 next[j] = x 成立,则表示如果主串的第i个字符和模式串的第j个字符不匹配时,下次匹配是让主串的第i个字符和模式串的第x个字符开始匹配。
条件next[j] = x 还表示,对于模式串的第j个字符,如果存在一个最大区间t,使得模式串区间[0,t-1] 和 区间[j - t,j-1]中的字符相等。此时 x是等于 t (字符串下标从0开始)。即在进行下一次匹配时,可以把模式串区间[0,t-1]之间的字符不进行比较,略过这个区间,直接跳到下标为t个字符(第t+1个字符)进行比较。
代码:
int KMP(const char* strTarget,const char* strPattern,int next[])
{
assert(strTarget && strPattern);
int nCurTar = 0;
int nCurPat = 0;
int nTargetLen = strlen(strTarget);
int nPatternLen = strlen(strPattern);
while (nCurTar < nTargetLen && nCurPat < nPatternLen)
{
if (-1 == nCurPat || strTarget[nCurTar] == strPattern[nCurPat])
{
//模式串和主串指针均往前走,继续下一次匹配的情况有两种:
//1、主串第nCurTar个字符与模式串第nCurPat个字符相等,此时需要比较下一个字符
//2、模式串第nCurPat字符,不存在一个t值,满足要求,已经无路可退。此时主串从nCurTar开始的字符肯定不会与模式串匹配。
nCurTar++;
nCurPat++;
}
else
{
//主串第nCurTar个字符与模式串第nCurPat个字符不相等,此时模式串回溯到第next[nCurPat]进行匹配
nCurPat = next[nCurPat];
}
}
if (nCurPat == nPatternLen) //匹配成功
{
assert(nCurTar - nPatternLen >= 0);
return nCurTar - nPatternLen;
}
return -1;
}
注意:
初始化next数组
代码:
void GetNext(const char* strPattern,int next[])
{
assert(strPattern && next);
int nCurPat = 1;
int nLastPos = -1;
int nPatternLen = strlen(strPattern);
next[0] = -1;
while (nCurPat < nPatternLen)
{
if (-1 == nLastPos || strPattern[nCurPat - 1] == strPattern[nLastPos])
{
next[nCurPat] = ++nLastPos;
nCurPat++;
}
else
{
nLastPos = next[nLastPos];
}
}
}next数组的优化
void GetNext(const char* strPattern,int next[])
{
assert(strPattern && next);
int nCurPat = 1;
int nLastPos = -1;
int nPatternLen = strlen(strPattern);
next[0] = -1;
while (nCurPat < nPatternLen)
{
if (-1 == nLastPos || strPattern[nCurPat - 1] == strPattern[nLastPos])
{
++nLastPos;//此时,nLastPos与正在处理的字符匹配的位置,nCurPat指向目前正在处理的字符
if (strPattern[nCurPat] != strPattern[nLastPos])
{
next[nCurPat] = nLastPos;
}
else
{
next[nCurPat] = next[nLastPos];
}
++nCurPat;
}
else
{
nLastPos = next[nLastPos];
}
}
}
当模式串和主串不匹配时,模式串下一次比较的起始位置是需要在运行之前预处理得到。
在匹配之前,对模式串进行预处理。在匹配时,如果匹配失败,不用回过头重新比较主串中的字符(不用回溯主串的指针),而是利用部分匹配的结果和模式串的预处理信息,确定从模式串的哪一个字符重新开始比较,而尽可能地减少匹配次数。
如果我们找到这个t之后,当主串的第i个字符与模式串的第j个字符不匹配时,可以直接让主串的第i个字符与模式串的第t个字符开始匹配即可。
每当一趟匹配过程中出现字符比较不等时,不需回溯主串指针,而仅仅移动模式串,从而尽可能地减少比较次数。
而是利用已经得到的部分匹配的结果,将模式串向右滑动尽可能远的一段距离后,继续进行比较,而尽可能地减少比较次数。