B. Squares

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Vasya has found a piece of paper with a coordinate system written on it. There are n distinct squares drawn in this coordinate system. Let's number the squares with integers from 1 to n. It turned out that points with coordinates (0, 0) and (a_i, a_i) are the opposite corners of the i-th square.

Vasya wants to find such integer point (with integer coordinates) of the plane, that belongs to exactly k drawn squares. We'll say that a point belongs to a square, if the point is located either inside the square, or on its boundary.

Help Vasya find a point that would meet the described limits.

Input

The first line contains two space-separated integers n, k (1 ≤ n, k ≤ 50). The second line contains space-separated integersa₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹).

It is guaranteed that all given squares are distinct.

Output

In a single line print two space-separated integers x and y (0 ≤ x, y ≤ 10⁹) — the coordinates of the point that belongs to exactly k squares. If there are multiple answers, you are allowed to print any of them.

If there is no answer, print "-1" (without the quotes).

Sample test(s)

input

4 3
5 1 3 4

output

2 1

input

3 1
2 4 1

output

4 0

input

4 50
5 1 10 2

output

-1

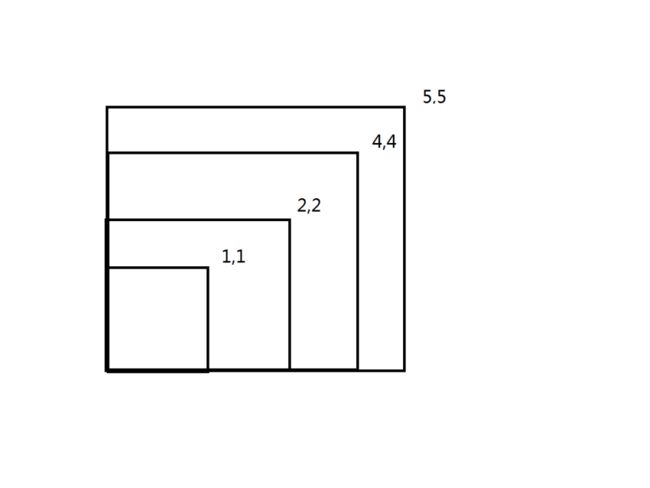
解题说明：此题其实就是n个正方形嵌套问题，要求在第k个区域内的点其实就是求第k大的正方形面积内的点（排除比他更小的正方形区域内的点），如下图所示，如果k为2，就是求第二个大正方形的点，内部点，边界都可以，由于题目说任意点均可，为了简单，我们完全可以取顶点，也就是（4,4）这点。最终题目就变成对一列数排序，输出第k大的数（k小于n），否则为-1。

#include <iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;

int main()
{
	int n,k,i,j;
	int a[51];
	int temp1;
	scanf("%d %d",&n,&k);
	for(i=0;i<n;i++)
	{
		scanf("%d",&a[i]);
	}
	if(k>n)
	{
		printf("-1\n");
	}
	else
	{
		for(i=0;i<n;i++)
		{
			for(j=i+1;j<n;j++)
			{
				if(a[j]>a[i])
				{
					temp1=a[i];
					a[i]=a[j];
					a[j]=temp1;
				}
			}
		}
		printf("%d %d\n",a[k-1],a[k-1]);
	}
	return 0;
}