牛顿迭代法求根——C语言
牛顿迭代法求根的原理:
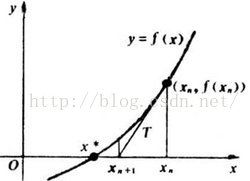
设r是
的根,选取
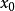 作为r的初始近似值,过点
作为r的初始近似值,过点
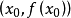 做曲线
做曲线
 的切线L,L的方程为
的切线L,L的方程为
 ,求出L与x轴交点的横坐标
,称x
1为r的一次近似值。过点
,求出L与x轴交点的横坐标
,称x
1为r的一次近似值。过点
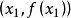 做曲线
做曲线
 的切线,并求该切线与x轴交点的横坐标
,称
的切线,并求该切线与x轴交点的横坐标
,称
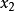 为r的二次近似值。重复以上过程,得r的近似值序列,其中,
称为r的
为r的二次近似值。重复以上过程,得r的近似值序列,其中,
称为r的
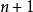 次近似值,上式称为
牛顿迭代公式。
次近似值,上式称为
牛顿迭代公式。
用牛顿迭代法解非线性方程,是把非线性方程
线性化的一种近似方法。把
在点
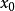 的某邻域内展开成泰勒级数
,取其线性部分(即泰勒展开的前两项),并令其等于0,即
的某邻域内展开成泰勒级数
,取其线性部分(即泰勒展开的前两项),并令其等于0,即
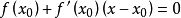 ,以此作为非线性方程
的近似方程,若
,以此作为非线性方程
的近似方程,若
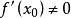 ,则其解为
, 这样,得到牛顿迭代法的一个迭代关系式:
。
,则其解为
, 这样,得到牛顿迭代法的一个迭代关系式:
。
题目:用牛顿迭代法求根。方程为
ax3+bx2+cx+d=0 。系数a,b,c,d的值一次为1,2,3,4,由主函数输入。求x在1附近的一个实根。求出根后由主函数输出。结果保留两位小数。
分析:该题目要求我们求1附近的一个实根,其实不管是在哪个数字附近,只要有while(fabs(x-x0)>=1e-5)这个条件就能够得到一个比较准确的近似值(如果不明白可以随便找几个数试一下,一定要按照牛顿迭代法的步骤来)。由分析得,我们一直是在求两点之间的距离,首先我们用到了xn这个点,通过数学关系,我们得到了xn+1这个点;然后我们又由xn+1这个点得到了一个更加接近于x*的点,接下来就是计算机枯燥的重复了,但是我们不能一直让它这么持续下去,所以我们加入了一个使循环结束的条件就是两点之间的距离无线下while(fabs(x-x0)>=1e-5)。分析得到,我们需要两个double型的存储空间。
#include<stdio.h>
#include<math.h>
int main()
{
double solut(double,double,double,double );//函数原型声明
double a,b,c,d;
scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
printf("%.2f",solut(a,b,c,d));
return 0;
}
double solut(double a,double b,double c,double d)
{
double x=1,x0;
do
{
x0=x;
x=x0-(((a*x+b)*x+c)*x+d)/((3*a*x+2*b)*x+c);
}
while(fabs(x-x0)>=1e-5);//为点xn+1与xn之间的距离,当两点的距离无限接近于0时,就时我们所要求的根x*。如果取x*这个点为例,我们发现方程在该点的切线与x轴的交点为x*,此时x与x0之间的距离为零。
return x;
}这个题目用到迭代法,说实话我的脑子转的慢,我到现在还没有学好这个方法。
迭代法的类似题目:
1:迭代法求两个数的最大公约数(辗转相除法)
原理:设两数为a、b(a>b),用a除以b,得a÷b=q......r1(0≤r1)。若r1=0,则(a,b)=b;若r1≠0,则再用b除以r1,得b÷r1=q......r2 (0≤r2).若r2=0,则(a,b)=r1,若r2≠0,则继 续用r1除r2,……如此下去,直到能整除为止。当然a与b的大小并不需要在意,因为在第一次辗转相除后,二者的位置关系就发生了改变。
#include <stdio.h>
#include <stdlib.h>
int main()
{
int a,b;
scanf("%d %d",&a,&b);
int maxgys(int a,int b);//函数原型声明
printf("%d",maxgys(a,b));
return 0;
}
int maxgys(int a,int b)
{
while(b!=0)
{
int r;
r=a%b;
a=b;
b=r;
}
return a;
}
2:Fibonacci数列也可以用到迭代法
原理:斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用。
#include <stdio.h>
#include <stdlib.h>
int main()
{
long n;
scanf("%ld",&n);
void fibonacci(long);
fibonacci(n);
return 0;
}
void fibonacci(long n)
{
long f1,f2,fn,i;
f1=1;
f2=2;
printf("%ld %ld ",f1,f2);
for(i=1;i<=n-2;i++)
{
fn=f1+f2;
f1=f2;
f2=fn;
printf("%ld",f2);
printf(" ");
}
}