两个函数连续性的讨论
、
notice the 1/2 is the only rational number reduce to lowest terms with denominator 2 and belonging to [0,1];
注意:有理数1/2是唯一化解到最低项,并且分母为2,属于区间[0,1]的有理数
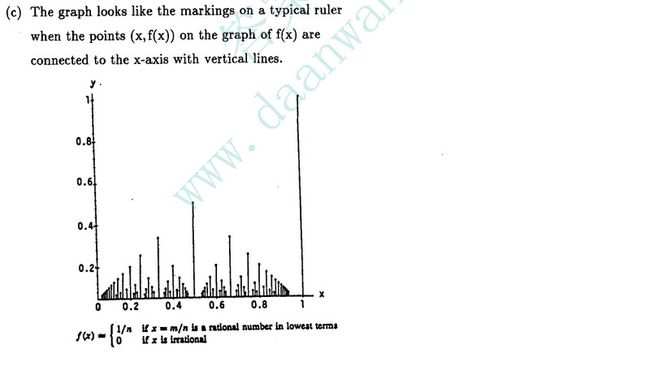
16题,dirichlet直尺函数在区间[0,1]的无理数点上连续
在irrational 点上f(c)=0, 其次我们选定ε>0 后, 令1/N <ε,
在[0,1]区间内分母<N的有理数个数是有限的(也就是说 当分母r<N 那么f(mr/r)=1/r后 1/r > 1/N >ε的有理数个数是有限的)
比方选 1/4后,有理数有 1/1,1/2,1/3,2/3,3/3,1/4,3/4,4/4 个,现在选择N,那么领这些有理数为 r1,r2,r3.....rp (注意通过上面的分析 p>N,注意这里r1~rp是列出了小于分母小于N的全部有理数,当然分子是1~(N-1) 即 1~(N-1)/1~N 个)
现在选择δ为min{|c-ri|i=1,2,3,4...,p} (即1/r >1/N>ε --(可能大于ε) 的有理数中的与c距离最短的那个有理数),那么在这个区间中[c-δ,c+δ]中就不会再存在
一个r 其1/r>1/N从而可能>ε,( 当然在[c-δ,c+δ]区间中会存在无数多个分母>N的有理数 rr,但是 1/rr <1/N) 从而保证了 |f(x)-f(c)|=|f(x)-0|<1/N<ε 只要按上面的方式选取δ