基于OpenCV平滑图像

基于OpenCV平滑图像也就是图像模糊，本博文介绍使用OpenCV的不同函数通过线性滤波进行图像平滑。

cv::blur
cv::GaussianBlur　（高斯模糊）
cv::medianBlur　（中值模糊）
cv::bilateralFilter　（双边滤波）

理论

进行图像平滑的目的有很多，本文的目的是减少噪音。

线性滤波为最常用滤波方式, 输出像素的值 g(i,j) 　取决于一组输入像素 f(i+k,j+l) 的加权和:

• g(i,j)=∑k,lf(i+k,j+l)h(k,l)

  其中，h(k,l) 　　　被称为核（滤波器的系数）.也就是一个滑动窗.

归一化块滤波器

最简单的滤波器，每一个像素的输出值，是其核决定的相邻像素的均值。核的形式如下：

• K=1Kwidth⋅Kheight⎡⎣⎢⎢⎢⎢⎢11..111..111..1...............11111⎤⎦⎥⎥⎥⎥⎥

高斯滤波

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

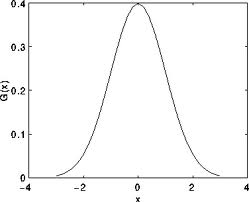
可能是最有用的滤波器 (不是最快的).高斯滤波是通过像素点和高斯核卷积和实现。通过下图作说明，还记得 1维 高斯核像什么么?

• 
  

  假设图像是1维的, 可以看到排在中间位置的像素具有最大的权重. 相邻像素的权因子随着和中心像素的距离的增大递减。

  备注：

   2维高斯核函数可以表示为 :

  G0(x,y)=Ae−(x−μx)22σ2x+−(y−μy)22σ2y

  
  

  其中 μ 是均值 (the peak) ， σ 表示方差 (per each of the variables x and y )

中值滤波

中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术，中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替，让周围的像素值接近的真实值，从而消除孤立的噪声点。中值滤波对脉冲噪声有良好的滤除作用，特别是在滤除噪声的同时，能够保护信号的边缘，使之不被模糊。这些优良特性是线性滤波方法所不具有的。

双边滤波

目前为止，已经介绍了一些图像平滑方法，虽然消除了噪声但是同事也平滑了边缘。为了避免平滑边缘可以使用双边滤波。

双边滤波（Bilateral filter）是一种非线性的滤波方法，是结合图像的空间邻近度和像素值相似度的一种折衷处理，同时考虑空域信息和灰度相似性，达到保边去噪的目的。具有简单、非迭代、局部的特点。
双边滤波器的好处是可以做边缘保存（edge preserving），一般过去用的维纳滤波或者高斯滤波去降噪，都会较明显地模糊边缘，对于高频细节的保护效果并不明显。双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma－d，它是基于空间分布的高斯滤波函数，所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素值，这样就保证了边缘附近像素值的保存。但是由于保存了过多的高频信息，对于彩色图像里的高频噪声，双边滤波器不能够干净的滤掉，只能够对于低频信息进行较好的滤波。

和高斯滤波器类似，双边滤波器也考虑相邻的像素分配的权重。这些权重有两个组成部分，第一个是高斯滤波器相同权权重。第二个是考虑相邻像素之间的强度的差异和评价。

详细的介绍参见这里 this link

代码

打开一副图像并应用４种平滑方法。

/**
 * file Smoothing.cpp
 * brief Sample code for simple filters
 * author OpenCV team
 */

#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"

using namespace std;
using namespace cv;

/// Global Variables
int DELAY_CAPTION = 1500;
int DELAY_BLUR = 100;
int MAX_KERNEL_LENGTH = 31;

Mat src; Mat dst;
char window_name[] = "Smoothing Demo";

/// Function headers
int display_caption( const char* caption );
int display_dst( int delay );


/**
 * function main
 */
int main( void )
{
  namedWindow( window_name, WINDOW_AUTOSIZE );

  /// Load the source image
  src = imread( "lena.jpg", IMREAD_COLOR );

  if( display_caption( "Original Image" ) != 0 ) { return 0; }

  dst = src.clone();
  if( display_dst( DELAY_CAPTION ) != 0 ) { return 0; }


  /// Applying Homogeneous blur
  if( display_caption( "Homogeneous Blur" ) != 0 ) { return 0; }

  //![齐次模糊]
  for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
      { blur( src, dst, Size( i, i ), Point(-1,-1) );
        if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }
  //![blur]

  /// Applying Gaussian blur
  if( display_caption( "Gaussian Blur" ) != 0 ) { return 0; }

  //![高斯滤波]
  for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
      { GaussianBlur( src, dst, Size( i, i ), 0, 0 );
        if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }
  //![高斯滤波]

  /// Applying Median blur
  if( display_caption( "Median Blur" ) != 0 ) { return 0; }

  //![中值滤波]
  for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
      { medianBlur ( src, dst, i );
        if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }
  //![中值滤波]

  /// Applying Bilateral Filter
  if( display_caption( "Bilateral Blur" ) != 0 ) { return 0; }

  //![双边滤波]
  for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
      { bilateralFilter ( src, dst, i, i*2, i/2 );
        if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }
  //![双边滤波]

  /// Wait until user press a key
  display_caption( "End: Press a key!" );

  waitKey(0);

  return 0;
}

/**
 * @function display_caption
 */
int display_caption( const char* caption )
{
  dst = Mat::zeros( src.size(), src.type() );
  putText( dst, caption,
           Point( src.cols/4, src.rows/2),
           FONT_HERSHEY_COMPLEX, 1, Scalar(255, 255, 255) );

  imshow( window_name, dst );
  int c = waitKey( DELAY_CAPTION );
  if( c >= 0 ) { return -1; }
  return 0;
}

/**
 * @function display_dst
 */
int display_dst( int delay )
{
  imshow( window_name, dst );
  int c = waitKey ( delay );
  if( c >= 0 ) { return -1; }
  return 0;
}