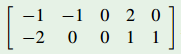矩阵分析与应用
七月在线4月机器学习算法班课程笔记——No.3
前言
第三讲依然是数学,因为数学是解决一切问题的基础,一个问深入到最后都是数理知识的支撑。所谓基础决定上层建筑,比如参加ACM比赛,高手之间的比赛已经不是编程技巧了,更多的是数学知识的比拼。若想走得远,数学基础一定要打好。嗯,好遗憾之前学数学多是为了考试,学完就忘,现在要好好再复习一下。程博士用两个小时概讲了《线性代数》《矩阵论》两本书的内容,结合其他的相关资料,总结一下。
1. 线性代数概念回顾
在听课之前,重新翻了一遍本科的《线性代数》,温习了线性代数中的重要概念,为了后面能够更深入的学习。
逆矩阵:对于n阶矩阵A,如果有一个n阶矩阵B,使 AB = BA = E, 则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵。当 |A| =0 时,A称为奇异矩阵。可逆矩阵一定是非奇异矩阵,因为矩阵可逆的充分必要条件是 |A|不为0.
矩阵的秩:矩阵A的行阶梯形中非零行的行数,就是矩阵A的秩。 对于n阶矩阵A,由于A的n阶子式只有一个|A|,故当 |A|不为0时R(A)=n,当|A|=0时R(A)<n。因此,可逆矩阵的秩 = 矩阵的阶数,不可逆矩阵的秩 < 矩阵的阶数。那么秩有什么实际意义吗?答案是肯定的。在做矩阵SVD分解的时候用于降噪,如果矩阵秩远小于样本维数(即矩阵列数),那么这些样本相当于只生活在外围空间中的一个低维子空间,这样就能实施降维操作。再者,如果把矩阵看成线性映射,那么秩就是象空间的的维数。
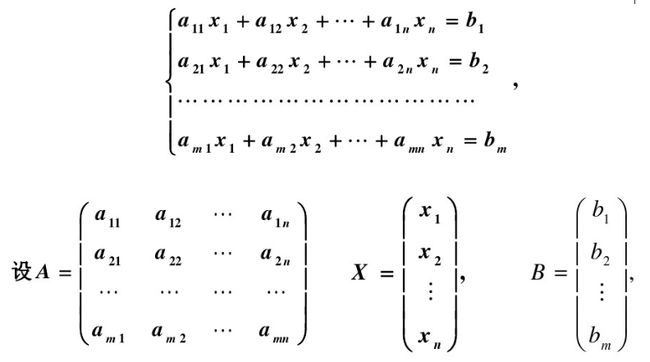
线性方程组的解:矩阵在数学上的基本的应用就是解线性方程组,这也是贯穿整个课本的样例。一个复杂的线性方程组可以表示为Ax=b,其中x,b是向量。通过求A的秩可以判定方程组的解:无解的充分必要条件是R(A) < R(A,b);有唯一解的充分必要条件是R(A) = R(A,b) = n;有无限多解的充分必要条件是R(A) = R(A,b) < n。
向量空间的基:设V是一个向量空间,V上有r个向量a1,a2...ar,并且满足 a1,a2...ar线性无关,并且V中的任一向量都可以由a1,a2...ar线性表示,那么向量组a1,a2...ar就称为向量空间V的一个基,r是向量空间的维数,并称V为r维向量空间。可以这么理解,把向量空间看做是向量组,那么基就是一个极大线性无关组,可以用来表示其他向量的最小组合,维数就是向量组的秩。
特征值与特征向量:对于n阶矩阵A,如果数 λ 和 n 维非零列向量 x 使关系式 Ax=λ x 成立,那么 λ 称为矩阵A的特征值,向量 x 就是A的对应于λ 的特征向量。那么如何理解特征值与特征向量呢?
我们知道,矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。实际上,这段话既讲了矩阵变换特征值及特征向量的几何意义(图形变换)也讲了其物理含义。物理的含义就是运动的图景:特征向量在一个矩阵的作用下作伸缩运动,伸缩的幅度由特征值确定。特征值大于1,所有属于此特征值的特征向量身形暴长;特征值大于0小于1,特征向量身形猛缩;特征值小于0,特征向量缩过了界,反方向到0点那边去了。
相似矩阵:设A,B都是n阶矩阵,若有可逆矩阵P,使P-1 AP=B,则B是A的相似矩阵。
对角阵:是一个主对角线之外的元素皆为 0 的矩阵。对角线上的元素可以为 0 或其他值。
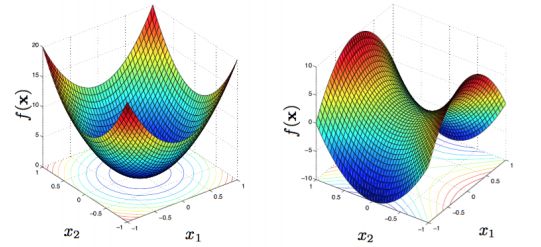
二次型:含有n个变量的二次齐次函数叫做二次型。只含平方项叫做二次型的标准型。用矩阵表示二次型就是f = xT Ax,A为对称矩阵。
2. 线性代数基本知识(新视角)
2.1 矩阵
下面跟着程老师再看线性代数。首先是矩阵,对矩阵的直观的理解源于《线性代数》课本中用矩阵表示线性方程组,今天我们分别从行视图和列视图的角度分析矩阵。例如矩阵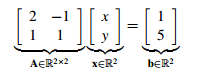 构成行视图的方程组为 2x-y=1;x+y=5,表示的是二维平面的两条直线,方程组的解就是两条直线的交点。
构成行视图的方程组为 2x-y=1;x+y=5,表示的是二维平面的两条直线,方程组的解就是两条直线的交点。
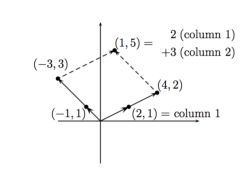
如果用列视图表达,就是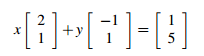 ,表示了两个向量之间的关系,如下图,有向量a(2,1)和向量b(-1,1),2a+3b=(1,5)。
,表示了两个向量之间的关系,如下图,有向量a(2,1)和向量b(-1,1),2a+3b=(1,5)。
这里我们来探究一下“维度”。数学中的维度和物理研究的维度不可一概而论。数学的维度表示的是独立参数的数目,物理学的维度指的是独立的时空坐标的数目。根据爱因斯坦的理论,我们生活的空间是四维空间,包含了三维的空间+时间。
2.2 线性相关和线性无关
我们先看线性相关和线性无关的定义。在向量空间V的一组向量A,如果存在不全为零的数 k1, k2, ···,km , 使![]() 则称向量组A是线性相关的,否则数 k1, k2, ···,km全为0时,称它是线性无关。线性无关可以这么理解,如果是二维空间,这组向量的任意两个向量不共线;如果是三维空间,则任意三个向量不共面,如果共面了就可以用另外两个表示第三个向量了不是么。
则称向量组A是线性相关的,否则数 k1, k2, ···,km全为0时,称它是线性无关。线性无关可以这么理解,如果是二维空间,这组向量的任意两个向量不共线;如果是三维空间,则任意三个向量不共面,如果共面了就可以用另外两个表示第三个向量了不是么。
2.3 向量空间的基
基:向量空间V的一组向量若满足(1)线性无关,(2)V中任一向量可由此向量线性表出,则称该组向量V中的一个基(亦称基底)。