数据结构——线索化二叉树

将二叉树变为线索二叉树的过程称为线索化。
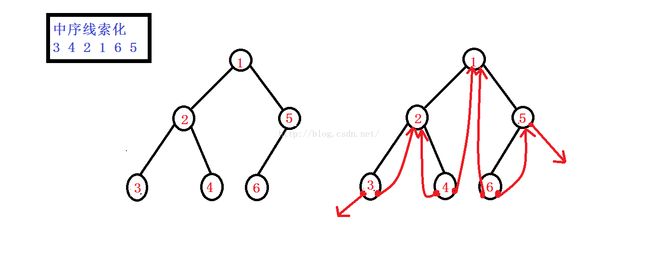
按某种次序将二叉树线索化的实质是：按该次序遍历二叉树，在遍历过程中用线索取代空指针。

算法根据二叉树遍历的方式而定。只需要将遍历算法中访问结点的操作具体化为建立正在访问的结点与其非空中序前趋结点间线索。
该算法应附设一个指针pre始终指向刚刚访问过的结点（pre的初值应为NULL），而指针p指示当前正在访问的结点。结点*pre是结点*p的前趋，而*p是*pre的后继。

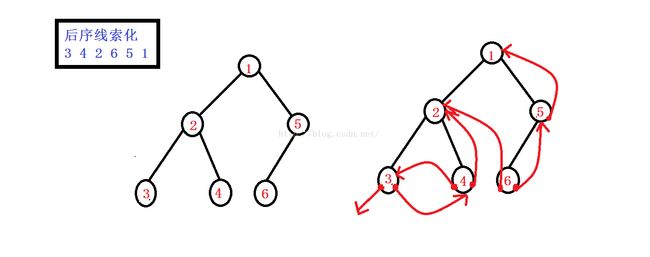
前序线索化和后序线索化算法与二叉树的中序线索化类似。

“BinaryTreeThd.h”

#pragma once

enum PointerTag
{
	THREAD,
	LINK,
};

template<class T>
class BinaryTreeThdNode
{
public:
	BinaryTreeThdNode(const T& data)
		:_left(NULL)
		,_right(NULL)
		,_data(data)
		,_leftTag(LINK)
		,_rightTag(LINK)
	{}
public:
	BinaryTreeThdNode<T>* _left;
	BinaryTreeThdNode<T>* _right;
	T _data;
	PointerTag _leftTag;
	PointerTag _rightTag;
};

template<class T>
class BinaryTreeThd
{
	typedef BinaryTreeThdNode<T> Node;
public:
	BinaryTreeThd(const T* arr,size_t size,const T& invalid)
	{
		size_t inder = 0;
		_root = _GreateTree(arr,size,invalid,inder);
	}
	void PrevOrderThreading()
	{
		Node* prev = NULL;
		_PrevOrderThreading(_root,prev);
	}
	void InOrderThreading()
	{
		Node* prev = NULL;
		_InOrderThreading(_root,prev);
	}
	void PostOrderThreading()
	{
		Node* prev = NULL;
		_PostOrderThreading(_root,prev);
	}
	void InOrder()//递归
	{
		_InOrder(_root);
		cout<<endl;
	}
	void PrevOrder()//递归
	{
		_PrevOrder(_root);
		cout<<endl;
	}
	void PostOrder()//递归
	{
		_PostOrder(_root);
		cout<<endl;
	}
	void InOrderThd()
	{
		Node* cur = _root;

		while (cur)
		{
			while (cur->_leftTag == LINK)
			{
				cur = cur->_left;
			}

			cout<<cur->_data<<" ";

			while (cur->_rightTag == THREAD)
			{
				cur = cur->_right;
				cout<<cur->_data<<" ";
			}
			cur = cur->_right;
		}
		cout<<endl;
	}
	void PrevOrderThd()
	{
		Node* cur = _root;

		while (cur)
		{
			while (cur->_leftTag == LINK)
			{
				cout<<cur->_data<<" ";
				cur = cur->_left;
			}
			
			cout<<cur->_data<<" ";
			cur = cur->_right;
		}
		cout<<endl;
	}
private:
	void _PrevOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		cout<<root->_data<<" ";
		_PrevOrder(root->_left);
		_PrevOrder(root->_right);
	}
	void _InOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		_InOrder(root->_left);
		cout<<root->_data<<" ";
		_InOrder(root->_right);
	}
	void _PostOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		_PostOrder(root->_left);
		_PostOrder(root->_right);
		cout<<root->_data<<" ";
	}
	void _PrevOrderThreading(Node* cur,Node*& prev)
	{
		if (cur == NULL)
		{
			return;
		}

		if (cur->_left == NULL)
		{
			cur->_leftTag = THREAD;
			cur->_left = prev;
		}

		if (prev && (prev->_right == NULL))
		{
			prev->_rightTag = THREAD;
			prev->_right = cur;
		}

		prev = cur;

		if (cur->_leftTag == LINK)
		{
			_PrevOrderThreading(cur->_left,prev);
		}
		if (cur->_rightTag == LINK)
		{
			_PrevOrderThreading(cur->_right,prev);
		}
	}
	void _InOrderThreading(Node* cur,Node*& prev)
	{
		if (cur == NULL)
		{
			return;
		}

		_InOrderThreading(cur->_left,prev);

		if (cur->_left == NULL)
		{
			cur->_leftTag = THREAD;
			cur->_left = prev;
		}

		if (prev && (prev->_right == NULL))
		{
			prev->_rightTag = THREAD;
			prev->_right = cur;
		}
		
		prev = cur;

		_InOrderThreading(cur->_right,prev);
	}
	void _PostOrderThreading(Node* cur,Node*& prev)
	{
	}
	Node* _GreateTree(const T* arr,size_t size,const T& invalid,size_t& inder)
	{
		Node* root = NULL;
		if ((inder < size) && (arr[inder] != invalid))
		{
			root = new Node(arr[inder]);

			root->_left = _GreateTree(arr,size,invalid,++inder);
			root->_right = _GreateTree(arr,size,invalid,++inder);
		}
		return root;//返回根节点
	}
private:
	Node* _root;
};

“test.cpp”

#define _CRT_SECURE_NO_WARNINGS 1

#include <iostream>
using namespace std;
#include "BinaryTreeThd.h"

void Test()
{
	int arr1[10] = {1, 2, 3, '#', '#', 4, '#' , '#', 5, 6};
	int size1 = sizeof(arr1)/sizeof(arr1[0]);
	BinaryTreeThd<int> t1(arr1,size1,'#');

	cout<<"前序遍历： ";
	t1.PrevOrder();
	cout<<"中序遍历： ";
	t1.InOrder();
	cout<<"后序遍历： ";
	t1.PostOrder();

	t1.PrevOrderThreading();
	cout<<"（线索化）前序遍历： ";
	t1.PrevOrderThd();


	int arr2[10] = {1, 2, 3, '#', '#', 4, '#' , '#', 5, 6};
	int size2 = sizeof(arr2)/sizeof(arr2[0]);
	BinaryTreeThd<int> t2(arr2,size2,'#');

	cout<<endl;
	cout<<"前序遍历： ";
	t2.PrevOrder();
	cout<<"中序遍历： ";
	t2.InOrder();
	cout<<"后序遍历： ";
	t2.PostOrder();

	t2.InOrderThreading();
	cout<<"（线索化）中序遍历： ";
	t2.InOrderThd();
}

int main()
{
	Test();
	system("pause");
	return 0;
}