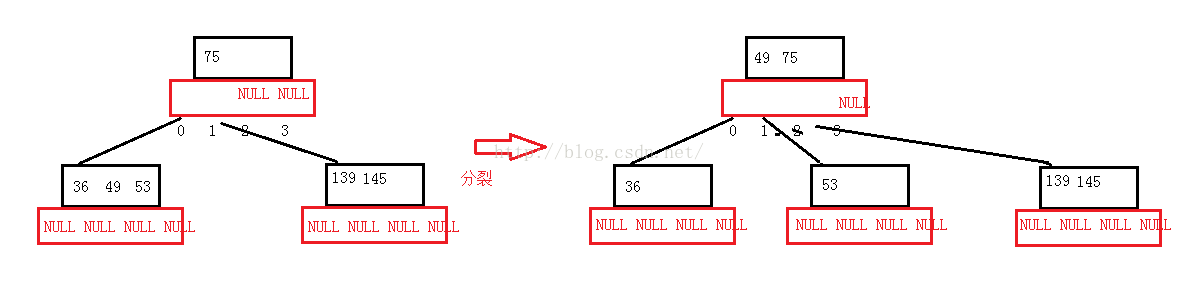
浅析B树的分裂过程

B-树>

     最近一直在研究树的这种数据结构，今天实现了一颗适合外查找的平衡多叉树就是B树，有的地方也叫B-树(不要误读为"B减树"奥).当然了还存在B+树，B*树这里只实现B树

 一.B-树的性质>

     一颗M阶(M>2)的B树，是一颗平衡的M路平衡搜索树，可以是空树或者满足下面几条性质>

     1).根结点至少有两个孩子.

     2).每个非根结点存在[M/2,M)个孩子.

     3).每个非根结点有[M/2-1,M-1)个关键字，且以升序排列.

      非根结点的孩子始终比非根结点的关键字多一个.

     4).对于一个关键字来说它的左孩子的下标一定和它一样，它的右孩子的下标一定比它多一个.

     5).所有的叶子结点都在同一层

 二.B-树的插入以及分裂的过程>

      B树的结点结构>

     

template<class K,int M>
struct BTreeNode
{
	//多给一个便于分裂
	K _keys[M];                //关键字数组
	BTreeNode<K,M> *_sub[M+1]; //链接子树的指针数组
	BTreeNode<K,M> *_parent;
	int _size;                 //关键字的个数
	BTreeNode()
		:_parent(NULL)
		,_size(0)
	{
		for (size_t i=0;i<M;++i)
		{
			_keys[i]=K();
			_sub[i]=NULL;
		}
		_sub[M]=NULL;
	}
};

 

     

     以M=3(3阶),{53,75,139,49,145,36,101}为例理解B树的插入>

     

     

    

     对于B树的插入过程>

      1).空树则直接新建结点.

      2).如果要插入的结点存在在该树中，不再插入.

      3).如果不存在且没满直接插入到对应的位置中.

      4).如果存在且满了则需要进行分裂(有的情况下可能进行多次分裂).

    B树的查找>

     1).确定返回类型>

      在插入新节点前我们需要查找要插入的数据是否在该树中则需要Find()这个函数，在这里用到了pair这个结构可以返回两种类型，因为新插入的结点既需要知道插入的地址也需要知道要插入到该地址的哪个下标中,而pair这个结构正好解决了这种问题.

     2).查找分析>

     如果要插入的结点存在则返回位置和对应下标

     如果要插入结点的关键字比当前的关键字大则找下一个下标

     如果比keys小去子树中查找

     当没有找到返回NULL容易导致异常故需要设计一个parent指针指向当前结点的父节点，如果没有找到则返回parent的位置和-1. 

   B树的中序遍历

     左-根-右

     不过此时的根结点的关键字是数组所以需要循环输出，又因为B树是M路的多叉树所以当递归了左和根之后其他的子节点域同样也需要递归处理.

  B树的代码实现>

      BTree.h

      

#define _CRT_SECURE_NO_WARNINGS 1

#pragma once

template<class K,int M>
struct BTreeNode
{
	//多给一个便于分裂
	K _keys[M];                //关键字数组
	BTreeNode<K,M> *_sub[M+1]; //链接子树的指针数组
	BTreeNode<K,M> *_parent;
	int _size;                 //关键字的个数
	BTreeNode()
		:_parent(NULL)
		,_size(0)
	{
		for (size_t i=0;i<M;++i)
		{
			_keys[i]=K();
			_sub[i]=NULL;
		}
		_sub[M]=NULL;
	}
};

template<class K,int M>
class BTree
{
	typedef BTreeNode<K,M> Node;
public:
	BTree()
		:_root(NULL)
	{}
	pair<Node *,int> Find(const K& key)
	{
		Node *cur=_root;
		Node *parent=NULL;
		while (cur)
		{
			int i=0;
			while (i < cur->_size)
			{
				if (cur->_keys[i] < key)
					++i;
				else if(cur->_keys[i] > key)
					break;
				else                         //找到了
					return pair<Node *,int>(cur,i);
			}
			parent=cur;
			cur=cur->_sub[i];
		}
		return pair<Node *,int>(parent,-1);   //没有找到
	}
	bool Insert(const K& key)
	{
		if (_root == NULL)     //空树
		{
			_root=new Node;
			_root->_keys[0]=key;
			_root->_size=1;
			return true;
		}
		pair<Node *,int> ret=Find(key);
		if(ret.second != -1)        //找到了不再插入
			return false;

		Node *cur=ret.first;
		Node *sub=NULL;
		K NewKey=key;
		while (1)
		{
			InsertKey(cur,NewKey,sub);
			if(cur->_size < M)    //如果cur没满则停止
				return true;
			//cur满,分裂，拷贝key和孩子
			size_t mid=cur->_size/2;
			Node *tmp=new Node;
			int j=0;
			for (int i=mid+1;i<cur->_size;++i)
			{
				tmp->_keys[j]=cur->_keys[i];
				//连续分裂
				if (cur->_sub[i])
				{
					tmp->_sub[j]=cur->_sub[i];
					tmp->_sub[j+1]=sub;
					cur->_sub[i]=NULL;
					tmp->_sub[j]->_parent=tmp;
					tmp->_sub[j+1]->_parent=tmp;
				}
				tmp->_size++;
				cur->_keys[i]=K();
				cur->_size--;
				j++;
			}
			if(cur->_parent == NULL)       //分裂到根结点
			{
				_root=new Node;
				_root->_keys[0]=cur->_keys[mid];
				_root->_sub[0]=cur;
				_root->_sub[1]=tmp;
				_root->_size++;
				cur->_keys[mid]=K();
				cur->_size--;

				tmp->_parent=_root; //链接
				cur->_parent=_root;
				return true;
			}
			//没有分裂到根结点
			NewKey=cur->_keys[mid];
			cur->_keys[mid]=K();
			cur->_size--;
			sub=tmp;
			cur=cur->_parent;
		}
		return true;
	}
	void InsertKey(Node *cur,const K& key,Node *sub)
	{
		int i=cur->_size-1;
		while (i >= 0)
		{
			if (cur->_keys[i] < key)
				break;
			else
			{
				cur->_keys[i+1]=cur->_keys[i];
				cur->_sub[i+2]=cur->_sub[i+1];
				--i;
			}
		}
		cur->_keys[i+1]=key;
		cur->_sub[i+2]=sub;
		if(sub)
			sub->_parent=cur;
		cur->_size++;
	}
	void InOrder()
	{
		_InOrder(_root);
		cout<<endl;
	}
public:
	void _InOrder(Node *root)
	{
		if(root == NULL)
			return ;
		_InOrder(root->_sub[0]);
		for (int i=0;i<root->_size;++i)
		{
			cout<<root->_keys[i]<<" ";
		}
		for (int i=1;i<M;++i)
		{
			_InOrder(root->_sub[i]);
		}
	}
protected:
	Node *_root;
};

void testBTree()
{
	int array[]={53, 75, 139, 49, 145, 36,101};
	int size=sizeof(array)/sizeof(array[0]);
	BTree<int,3> tree;
	for (int i=0;i<size;++i)
	{
		tree.Insert(array[i]);
	}
	tree.InOrder();
}