分散层叠（Fractional Cascading）

一、 引言

最初接触Fractional Cascading这个概念，应该是在计算几何中的Range Tree里。当然，限于篇幅本文并不打算对Range Tree做过深的讨论。但是我们仍然可以对Fractional Cascading这个思想来做一番详细的解读。

什么是Fractional Cascading，从字面意思上来说Fractional是零碎的、微小的，Cascade做名词的时候是小瀑布的意思，Cascading你可以形象地理解为像小瀑布一样的，或者层叠的。把这个名词整体翻译成中文确实比较难找到一个妥帖的对应，或者我们直接来理解这个算法思想本身更加实际。而且当你真的理解它之后，你自然就会体悟到这个名词的精髓所在。下面这张图是Fractional Cascading的提出者Chazelle 和 Guibas 在 1986年发表的著作开篇给出的一幅图画，它其实相当形象地揭示了这个名词背后的深刻含义。大概就是像瀑布一样从高到低逐渐分散成越来越细的支流，再层层叠叠的覆盖之意。

Chazelle 和 Guibas 在著作中认为Fractional Cascading是一个高效的策略for dealing with iterative searches that achieves optimal time in linear space。其他学者也下过类似的定义，认为Fractional Cascading是一个高效的策略for solving the multiple look-up query problems。那什么是iterative searches或者multiple look-up呢？

假设现在你有 k 个有序数列，其中第 i 个记作 Li , 这 k 个序列的总长度是 ∑ki=1| Li |=n 。例如下面的例子中， k=4 , n=17 。

L1=2.4, 6.4, 6.5, 8.0, 9.3 ;
L2=2.3, 2.5, 2.6 ;
L3=1.3, 4.4, 6.2, 6.6 ;
L4=1.1, 3.5, 4.6, 7.9, 8.1 ;

现在你的任务是查找 single element in each of the k arrays，如果不存在就返回它应该被插入的位置（或者它的前继或者后继，具体问题可以自由定义）。例如，假设你要找的是6.4，那么搜索 L1、L2、L3、L4 应该分别返回6.4，2.6，6.6， 4.6。那么，你会想到怎么解决这个问题呢？

Begin with a Straightforward Strategy

一种很简单的方法就是对每个List单独进行一次二分搜索，此时你的所需要的空间就是O(n)，也就是只要用有序表对原数据进行储存即可。时间复杂度是多少呢？ k 个有序表，平均每个列表中有 n/k 个节点，对每个表进行二分搜索的时间复杂度是 log(n/k) ，也是总共的时间复杂度就是 klog(n/k) 。

有没有更好的方法？我们可以考虑用“空间来换时间”。具体做法是将这个 k 个表归并成一个大的表 L ，然后给 L 中的每个元素 x 配上一个用来指示该元素在原来的每个 Li 中的位置（如果未出现，则为其应该被插入的位置）。比如我们采用 x[a,b,c,d] 的形式，那么 x 就是具体的数值， a,b,c,d 分别表示位置（位置从0开始计）。就之前的例子而言，我们便可以得到
L=1.1[0,0,0,0],1.3[0,0,0,1],2.3[0,0,1,1],2.4[0,1,1,1],
   2.5[1,1,1,1],2.6[1,2,1,1],3.5[1,3,1,1],4.4[1,3,1,2],
   4.6[1,3,2,2],6.2[1,3,2,3],6.4[1,3,3,3],6.5[2,3,3,3],
   6.6[3,3,3,3],7.9[3,3,4,3],8.0[3,3,4,4],8.1[4,3,4,4],9.3[4,3,4,5]
例如8.0[3,3,4,4]表示：在 L1 中，8.0位于位置3处（注意因为是从0开始的）；在 L2 中，因为8.0不存在，所以返回它应该被插入的位置，即位置3；同样，在 L3 中，因为8.0不存在，所以返回它应该被插入的位置，即位置4； L4 中的情况类似。

这个归并操作可以令时间复杂度降为 O(k+logn) ，因为在 L 中搜索 q 的时间显然是 logn ，报告结果的时间则为 k 。如果 q=5 ，那么在 L 中将会找到（这里我们规定如果找不到就返回第一个比其大的值） 6.2[1,3,2,3 ，由此我们再做一次直接访问（类似哈希）就可以获得 L1[1]=6.4 ， L2[3] （注意这是一个flag value表示 q 已经到达列表尾部。 L3[2]=6.2 以及 L4[3]=7.9 。

这个方法有没有什么问题呢？是的，它的空间复杂度过高，显然它的空间消耗为 O(kn) ，因为 L 中的 n 个项目必须存储一个长为 k 的搜索结果。

Fractional Cascading

基于之前的分析，我们想知道就这个问题而言，还有没有更好的 方法？答案是Fractional cascading就给为我们提供了一种更好方法，它的时间复杂度是 O(k+logn) ，但是它所需要的空间也仅仅只是 O(n) 。

Fractional cascading到底是怎么做到呢？本质上它也是要做归并，但是却并非归并全部！原来有 k 个有序表，生成之后的结构仍然是 k 个有序表，记为 Mi 。最后一个 Mk 就是 Lk 。前面的每一个列表 Mi 都是由原来的 Li 和 Mi+1 的部分归并而成，更具体的说是 Mi+1 的从第二个元素开始隔一个采样一个得到的子序列。同时，我们为每一个（归并后序列 Mi 中）元素 x 配上两个数字，第一个是 x 在原本 Li 中的位置，第二个是 x 在 Mi+1 中的位置。

仍然以前面的问题为例，我们将得到下面的结果：

M1=2.4[0,1],2.5[1,1],3.5[1,3],6.4[1,5],6.5[2,5],7.9[3,5],8.0[3,6],9.3[4,6]
M2=2.3[0,1],2.5[1,1],2.6[2,1],3.5[3,1],6.2[3,3],7.9[3,5]
M3=1.3[0,1],3.5[1,1],4.4[1,2],6.2[2,3],6.6[3,3],7.9[4,3]
M4=1.1[0,0],3.5[1,0],4.6[2,0],7.9[3,0],8.1[4,0]

下面的图示说明了 M3 是如何从 L3 和 M4 归并而成的：

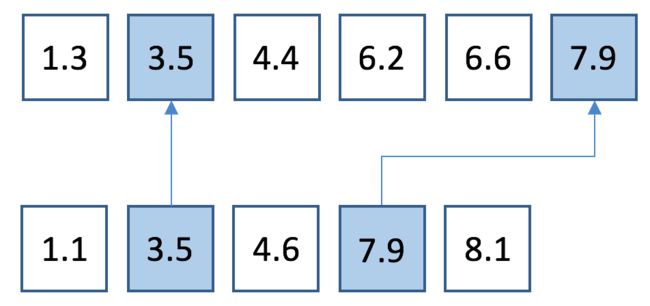
假设我们现在要执行搜索 q=5 ，我们首先在 M1 中执行标准的二分搜索 q （同样规定如果找不到就返回第一个比其大的值），所以返回6.4[1, 5]：其中的“1”告诉我们如果在 L1 中搜索 q 的时候，会返回 L1[1]=6.4 ；其中的“5”表示 q 在 M2 中的位置大约是5。 更确切地说，在 M2 中执行二分搜索 q 将会返回 7.9[3, 5] ，注意7.9[3, 5]在 M2 的位置就是 5, 或者更前面的一个位置也即是 6.2[3, 3]。将 q 与 6.2相比较，发现 q 更小，所以我们决定在 M2 中更加正确的位置应给是6.2[3, 3]。其中第一个数字 “3” 表示在 L2 中搜索 q 将会返回 L2[3] ，也就是一个 flag value，以为 q 已经到了列表 L2 的尾部。6.2[3, 3]中的第二个数字“3” 表示 q 在 M3 中的位置大约是3。更确切地说，在 M3 中用二分搜索法来查找 q 的话将会返回6.2[2, 3]，其位置就是 3（或者更前的一个位置也就是 4.4[1, 2] ）。将 q 与这两个值相比较之后我们知道更正确的值应该是 6.2[2,3]。其中的 “2” 表示在 L3 中搜索 q 将会返回 L3[2]=6.2 , 而 6.2[2,3]中的 “3” 表示在 M4 中搜索 q 将会得到 M4[3]=7.9[3,0] 或 M4[2]=4.6[2,0] ，相比较之后我们知道正确的值应该是 7.9[3,0]，而在 L4 中搜索 q 将会得到结果 L4[3]=7.9 。于是，我们便找到了 q 在全部四个列表中的位置。

整个过程可以总结为，先对 M1 做一次二分搜索，然后从所得之结果中判定 q 在 L1 中的位置。接下来，对于每一个 i>1 ，我们利用已知的 q 在 Mi 中的位置去找寻其在 Mi+1 中的位置。而 q 在 Mi 中的位置所给出的附加信息要么是 q 在 Mi+1 中的位置，要么离正确位置只差一步位移，所以紧跟着就是在其后的列表中执行一次比较。并如此继续下去。如此一来总共的查询时间就是 O(k+logn) 。

而且我们还可以证明这个数据结构所耗用的空间至多是

∑|Mi|=∑|Li|(1+12+14+⋯)≤2n=O(n)

在Range Tree中使用Fractional Cascading的一些初步讨论

鉴于篇幅有限，我们无法对Range Tree做详细介绍。此处仅简单点出Fractional Cascading中的使用。

如下图所示，每次跟 x 方向进行的划分其实都是把节点分成了两组，那么我们不妨就将数据按照 y 方向上的值组织成Fractional Cascading的结构。和之前不一样的地方是，这次我们将两个列表归并成一个的时候，并不是采样隔一个做一次采样的方式，而是借助 x 方向上的划分直接来生成。

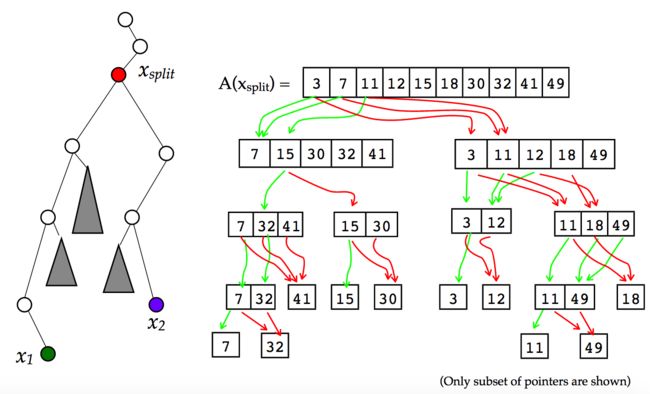
作为呼应，最后这张图，是否能让你将其同本文开始时给出的那张“瀑布”的图片联系起来？瀑布的水流就是这样逐渐被划分成更细的支流，然后层层叠叠地流下，这也就是Fractional Cascading思想的精髓。

参考文献

【1】https://www.cs.princeton.edu/~chazelle/pubs/FractionalCascading2.pdf
【2】http://www.hpl.hp.com/techreports/Compaq-DEC/SRC-RR-12.pdf
【3】https://en.wikipedia.org/wiki/Fractional_cascading#CITEREFLueker1978
【4】http://blog.ezyang.com/2012/03/you-could-have-invented-fractional-cascading/
【5】https://www.cs.umd.edu/class/spring2008/cmsc420/L21.RangeTrees.pdf