Real-Time Rendering-第五章 Visual Appearance

第五章 Visual Appearance（视觉外观）

“A good picture is equivalent to a good deed.”
—Vincent Van Gogh

当你渲染三维模型的图像时，模型不仅应该具有正确的几何形状，还应该具有期望的视觉外观。在很多情况下（但不是全部 - 见第11章）渲染的目标是达到 photorealism（如照片一般写实）的效果—这是一种非常接近真实物体照片的外观。为了达到这个目标，重要的是要使用真实世界作为指导。本章首先讨论一些实现现实世界中光源和材质交互的方法。并通过一个简单的光照和表面模型的示例，讲述如何使用可编程的shaders实现这样的模型示例。

本章的其余部分介绍了一些其他的技术，用于在模型上渲染一种真实世界的外观。主要包括transparency（透明效果），antialiasing（抗锯齿）以及compositing（合成技术）。

5.1 Visual Phenomena

通过对类似于图5.1所示的场景执行一次真实的渲染操作，有助于理解相关的物理现象。这些现象包括：

• 光线是由太阳或其他光源（自然光或人造光）发出的。
• 光线通过与场景中的物体进行交互；部分被物体吸收，部分被分散和并传播到新的方向。
• 最后，光被传感器（人眼，电子传感器，或胶片）所吸收。

图5.1 一张房间的照片，显示了一种光源和各种物体的交互现象。

在图5.1中，我们可以看到所有这三种现象的根据。首先，光是由台灯发出的，并直接传播到房间中的物体上。物体的表面会吸收一部分光线并将一些光线散射到新的方向。没有被物体表面吸收的光线会在环境中继续传播，并照射到其他的物体上。最后，在环境中传播的一小部分光线会进入用于捕获图像的传感器中，在该示例中指数码相机的电子传感器。

在下面的章节中，我们将讨论每一种现象，以及如何使用前面章节讲解的渲染管线和GPU shaders来描绘这些现象。

5.2 Light Sources

使用使用各种模型表示光线，比如几何射线，电磁波或光子（具有一些波性质的量子粒子）。无论把光线表示为何种形式，光始终是电磁辐射能量体—在物理空间中传播的电磁能。Light sources（光源）是发光的物体，而不是散射或吸收光线。

根据不同的渲染目的，可以使用多种不同的方式表示光源。在这一节，我们将讨论一个简单的光照模型—在第7.4节和第8章中我们将会讨论更复杂以及更丰富的光照模型。像太阳这种超远距离光源是最容易模拟的；这种光源所发出的光以单一的方向进行传播，并且在整个场景中是相同的。因此，我们称之为 directional lights（定向光）。为了渲染光照，我们使用位于world space中 light vector（光线向量） l 表示这种光源的方向。另外，我们总是假定在本书中用到的向量 l 的长度为1。对于directional lights，通常在应用程序中把 l 规范化（缩放到长度为1），以避免需要在shader运算过程中对其进行重新规范化。通常把light vector l 定义为指向光线传播方向的反方向（如图5.2）。很快我们就会在后面的章节中解释这个原因。

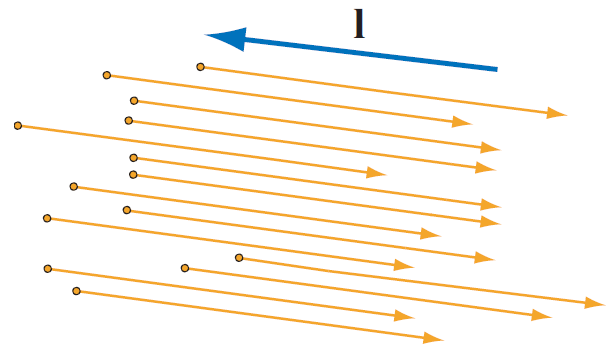
图5.2 light vector l 定义为指向光线传播方向的反方向

除了要指定光源的方向，还需要指定它发出的光照数量。关于光照的科学测量，radiometry（辐射测量技术），将在第7章7.1节讨论；本章将只会介绍相关的概念。通过测量穿过一个垂直于 l 的单位面积表面上的能量，可以量化定向光源的发射数量（如图5.3）。该数量称为 irradiance（辐照度），等于在一秒钟内穿过表面的光子能量的总和。另外，光是可以指定颜色的，因此我们可以把 irradiance 表示为包含三个数字的RGB向量：分别用于表示红色，绿色和蓝色（在7.3节中将会更详细的详解光照的颜色）。注意，不同于在应用程序中进行颜色绘制，irradiance中的RGB值可以超过1，理论上可以为任意大。

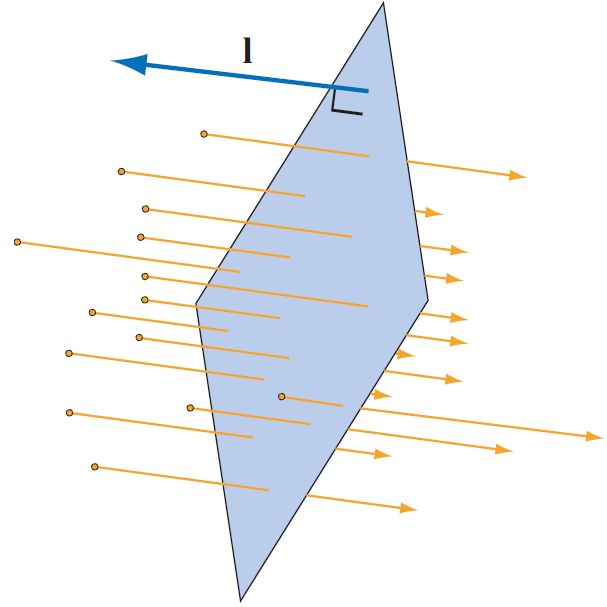
图5.3 测量定向光源发射的光的大小

即使在场景中只有一个主光源，被其他的物体和房间墙壁反弹的光线也会照亮物体。这类周围的或环境光被称为 ambient light（环境光）。在第8章和第9章我们将会讨论各种模拟环境光的方法，但为了简单，我们将不会在本章中讨论任何一种环境光。在我们这个简单的光照模型中，没有被直接照射到的表面是黑色的。

一般来说，尽管通过测量光源在垂直于 l 的平面上的 irradiance（辐射度）可以得知光照的亮度，但是要计算光源在表面上的 illumination（照明度），我们需要测量平行于该表面的一个平面上的辐射度（即垂直表面的法向量 n 。表面的辐射度等于在垂直于 l 乘以 l 和 l 夹角 θi 的余弦（如图5.4的左侧所示）方向上测量的辐射度。 在垂直于 l 上测量的辐射度，

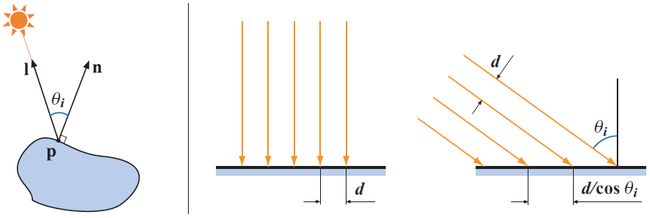
图5.4 左图中显示了光照的几何描述。中间图中表示光线垂直照射到表面上，右图中则是光线与表面形成一定的角度。

图5.4的中间和右边的图中描述了该余弦因子的几何解释。在中间图中是光线垂直照射表面的情况。辐照度与光线的密度成正比，而与光线到表面之间的距离 d 成反比。在这种情况下，表面的辐射度和垂直于 l 方向的辐射度是相同的。在右图中，光线照射自一个不同的方向。这些光线与平面的法线成 θi 角。此时，光线与表面之间的距离为 d/cosθi 。由于辐射度与该距离成反比，这就意味着辐射度必须与 cosθ 成正比。这个余弦值可以很容易在着色器中通过计算两个向量的点积得到（注意 l 和 n 的长度总是为 1 ）。在这里我们知道了为什么要把光照向量 l 定义成光传播方向的反方向；否则我们必须在执行点积运算之前对其取反。

通常在辐射公式中使用记号 E 表示垂直于 n 方向的辐射度。我们将使用 EL 表示垂直于 l 方向的辐射度。注意在光线从表面下方照射过来的时候，对应的余弦值为该余弦的负值。在这种情况下，光源无法照亮表面，所以我们将使用余弦的clamp把该值限定为非负值（使用 cos¯¯¯¯¯ 表示）：

E  =ELcos¯¯¯¯¯θi=ELmax(n⋅l,0).(5.1)

图5.5 测量照射自任意方向光源的辐射度。

在图5.3和5.4中，所有的光线都是以固定的方向传播。然而，光照的辐射度通常是测量任意方向上的光线。辐射度的定义还是一样的：在一秒钟内穿过单位面积的光照能量（如图5.5所示）。这个数量值与一个现实世界的设备相关：light meter（曝光表）。该仪表通过测量一组波长乘以光的感知曲线得到辐射度，因此可以计算出光线到达一个朝向某个特定方向的（小）区域的传感数量。

注意，辐射度具有累加的性质；从多个定向光源照射的总辐射度是所有单个辐射度的总和，

E=∑k=1nELkcos¯¯¯¯¯θik.(5.2)

其中 ELk 和 θik 是第 k 个定向光源的 EL 和 θi 的值。

5.3 材质

在渲染时，通常使用物体的表面来展现场景。而物体的表面又是通过将材质附加到场景中的模型上来描绘的。每种材质对应于一组 shader 程序，纹理，以及其他属性。这些属性用于模拟光与物体的交互作用。本节首先描述在现实世界中光与物质如何相互作用，然后提供一个简单的材质模型。第7章将会提出一个更通用的材质模型的处理方式。

基本上，所有光与物质的交互作用的只有两种现象：scattering（散射）和 absorption（吸收）。

注：自发光是第三种现象，这种物体属于上一节所讨论的光源。

当光线遇到任何类型的光学不连续的地方，就会发生散射现象。这可能是两种具有不同光学属性的物质之间的分界点，晶体结构的中断点，密度变化等。散射不会改变光线的数量—只会导致光线的传播方向发生改变。

吸收发生在物质的内部，并导致一些光能转化为另一种能量并消失。它减少了光线的数量，但不会影响传播的方向。

渲染中最重要的光学不连续性是空气和物体之间的交界处，出现在模型的表面。表面把光线散射到两组不同的方向：进入表面（refraction（折射）或 transmission（传播））和离开表面（reflection（反射））；具有描述如图5.6所示。

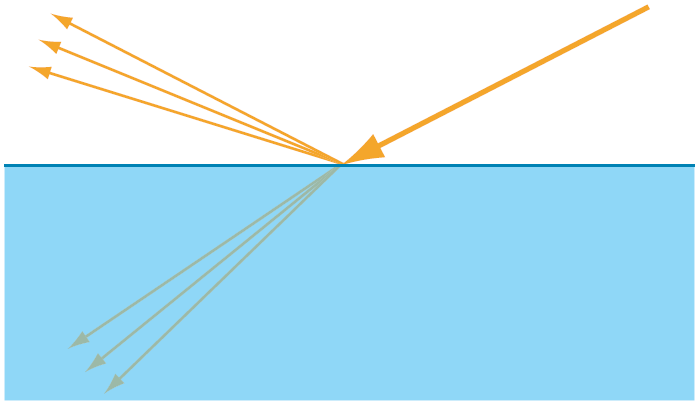
图5.6

如果是透明的物体，透射光会穿过物体继续传播。在第5.7节将会讨论一种简单的技术来渲染这样的物体；后面的章节中将会包含一些更高级的技术。在这一节我们只讨论不透明的物体，其中传播到物体上的光线经过多次散射和吸收事件，直到最后一些光线被表面重新发射出去（见图5.7）。

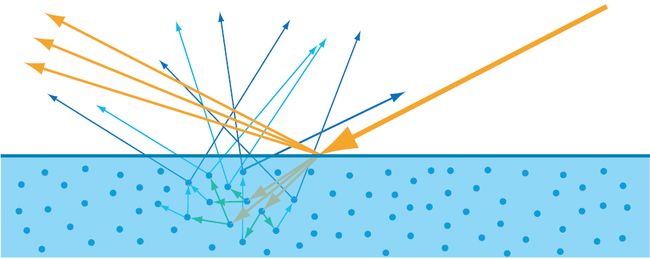
图5.7

如图5.7所示，已经在表面反射的光线与透射到表面内部，部分被吸收最后又被散射出表面的光线具有不同的方向分布和颜色。因此，通常把表面着色公式表示为两个单独的计算项。其中，specular term（镜面光计算项）表示被表面反射的光，则 diffuse term（漫反射光计算项）表示经过了透射，吸收和散射处理的光。

为了通过着色计算公式表征材质的行为，我们需要根据入射光的光线数量和方向表示反射光的数量和方向。

测量入射光的照明度与测量表面的辐射度方法一样。对于出射光的测量，我们是测量 exitance（出射度），类似于辐射度也是计算每秒钟穿过单位面积的光照能量。exitance 使用符号 M 表示。光照与物质的交互作用是线性的；加倍光照的辐照度会使出射度加倍。辐射度与出射度比值是材质的一种特性。对于那些自身不会发光的物体，这个比率始终介于 0 和 1 之间。不同颜色的光线，出射度和辐射度之间的比率也不同，因此把该比率表示为一个RGB向量或一种颜色，通常称为 surface color（表面的颜色） c 。为了表示这两种不同的光照项，着色公式中通常具有单独的 specular color（ cspec ）和 diffuse color（ cdiff ）计算项，其和为表面总的颜色 c 。由于 RGB 向量的分量值都是介于 0 和 1 之间，因此这些常规的颜色值都可以使用标准颜色选取界面，绘画应用等进行设置。另外表面的镜面光和漫反射光颜色取决于表面的成分，即是否由钢，彩色塑料，黄金，木，皮革等材料制成。