K-means均值聚类算法的原理与实现
转自:http://blog.csdn.net/xiaolewennofollow/article/details/45541159
K-均值聚类算法的原理与实现
聚类是一种无监督的学习,它将相似的对象归到同一个簇中,聚类方法几乎可以应用于所有对象,簇内的对象越相似,聚类的效果越好,本文主要介绍K-均值聚类的算法,之所以称之为K-均值是因为它可以发现k个不同的簇,并且每个簇的中心采用簇中所含的值的均值计算而成
K-均值聚类算法
- 优点:容易实现。
- 缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢
- 适用数据类型:数据型数据
k-均值是发现给定数据集的k个簇的算法,簇个数是由用户给定的,每一个簇通过质心(centroid),即簇中所有店的中心来描述。
k-均值算法的工作流程是这样的,首先,随机确定k个初始点作为质心。然后将数据集中的每个点分配到一个簇中,具体来说,为每个点找其最近的质心,并将其分配给质心所对应的簇,这一步完成后,每个簇的质心更新为该簇所有点的平均值。
上述过程的伪代码表示如下:
创建k个作为起始质心(通常是随机选择)
当任意一个点的簇分配结果发生改变时
对数据集中的每个数据点
对每个质心
计算质心与数据点之间的距离
将数据点分配到距离其最近的簇
对每一个簇,计算簇中所有点的均值并将均值作为质心
k-均值聚类的一般流程
- 收集数据:使用任意方法
- 准备数据:需要数据型数据来计算距离,也可以将标称型数据映射为二值型数据再用于距离计算。
- 分析数据:使用任意方法。
- 训练算法:不适用于无监督学习,即无监督学习没有训练过程。
- 测试算法:应用聚类算法,观察结果。可以使用量化的误差指标如误差平方和来评价算法的结果。
- 使用算法:可以用于所希望的任何应用,通常情况下,簇质心可以代表整个簇的数据来做出决策
上面提到的“最近”质心的说法,意味着需要进行某种距离计算,可以选择任意距离度量方法。这里我们选择利用欧式距离进行度量。数据集上的k-均值算法的性能会受到所选距离计算方法的影响。下面给出k-均值算法的代码实现,首先创建一个名为kMeans.py的文件,然后将下面程序清单中的代码添加到文件中。
首先我们需要k-均值聚类算法的支持函数,第一个函数loadDataSet(),它将原始数据文本文件读入到列表中,文本文件每一行为tab分隔的浮点数,每一个列表会被添加到dataMat中,最后返回dataMat,这种格式可以很容易将很多值封装到矩阵中。
def loadDataSet(fileName):
dataMat=[]
fr=open(fileName)
for line in fr.readlines():
curLine=line.strip().split('\t')
fltLine=map(float,curLine)
dataMat.append(fltLine)
return dataMat
我们首先使用testSet.txt文件中的实验数据,其中数据存储格式是这样的
vi testSet.txt
def distEclud(vecA,vecB):
return sqrt(sum(power(vecA-vecB,2)))
最后一个函数是randCent(),该函数为给定数据集构造一个包含k个随机质心的集合。随机质心必须要在整个数据集的边界之内,这个可以通过找到数据集的每一维的最小和最大值来完成。然后生成0到1.0之间的随机数并可以通过取值范围和最小值,以确保随机点在数据的边界之内
def kMeans(dataSet,k,distMeas=distEclud,createCent=randCent):
m=shape(dataSet)[0]
clusterAssment=mat(zeros((m,2)))
centroids=createCent(dataSet,k)
clusterChanged=True
while clusterChanged:
clusterChanged=False
for i in range(m):
minDist=inf;minIndex=-1
for j in range(k):
distJI=distMeas(centroids[j,:],dataSet[i,:])
if distJI<minDist:
minDist=distJI;minIndex=j
if clusterAssment[i,0]!=minIndex: clusterChanged=True
clusterAssment[i,:]=minIndex,minDist**2
print centroids
for cent in range(k):
ptsInClust=dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
centroids[cent,:]=mean(ptsInClust,axis=0)
return centroids,clusterAssment
kMeans()函数接受4个输入参数,只有数据集及簇的数目是必选参数,而用来计算距离和创建初始质心的函数都是可选的,kMeans()一开始确定数据集中数据点的总数,然后创建一个矩阵来存储每个簇的分配结果。簇分配结果矩阵clusterAssment包含两列:一列纪录簇索引值,第二列存储误差。这里的误差是指当前点到簇质心的距离。
按照上述方式(即计算之心-分配-重新计算)反复迭代,知道所有数据点的簇分配结果不再改变为止
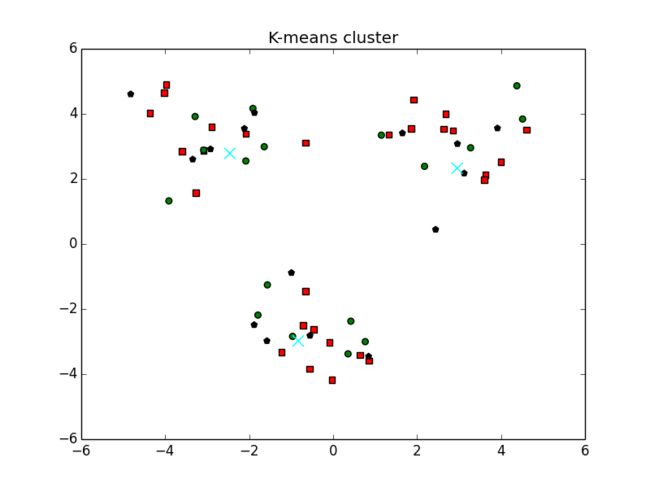
下图给出两个聚类结果的示意图,下面的图是一个由于质心随机初始化导致k-均值算法效果不好的一个例子,上面的图是一个包含三个簇的数据集上运行k-均值算法之后的结果,但是点的簇分配结果值没有那么准确,k-均值算法收敛单聚类效果较差的原因是,k-均值算法收敛到了局部最小值,而非全局最小值。
二分k-均值算法
为克服k-均值算法收敛于局部最小值的问题,有人提出了另一个称为二分k-均值的算法,该算法首先将所有点作为一个簇,然后将该簇一分为二,之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值,上述基于SSE的划分过程不断重复,知道得到用户指定的簇数目为止
二分k-均值算法的伪代码形式如下:
将所有点看成一个簇
当簇数目小于k时
对于每一个簇
计算总误差
在给定的簇上面进行k-均值聚类(k=2)
计算将该簇一分为二之后的总误差
选择使得误差最小的那个簇进行划分操作
def biKmeans(dataSet,k,distMeas=distEclud):
m=shape(dataSet)[0]
clusterAssment=mat(zeros((m,2)))
centroid0=mean(dataSet,axis=0).tolist()[0]
centList=[centroid0]
for j in range(m):
clusterAssment[j,1]=distMeas(mat(centroid0),dataSet[j,:])**2
while(len(centList)<k):
lowestSSE=inf
for i in range(len(centList)):
ptsInCurrCluster=dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]
centroidMat,splitClustAss=kMeans(ptsInCurrCluster,2,distMeas)
sseSplit=sum(splitClustAss[:,1])
sseNotSplit=sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
print sseSplit,sseNotSplit
if (sseSplit+sseNotSplit)<lowestSSE:
bestCentToSplit=i
bestNewCents=centroidMat
bestClustAss=splitClustAss.copy()
lowestSSE=sseSplit+sseNotSplit
bestClustAss[nonzero(bestClustAss[:,0].A==1)[0],0]=len(centList)
bestClustAss[nonzero(bestClustAss[:,1].A==0)[0],0]=bestCentToSplit
print 'the bestCentToSplit is', bestCentToSplit
print 'the len of bestClustAss is:',len(bestClustAss)
centList[bestCentToSplit]=bestNewCents[0,:]
centList.append(bestNewCents[1,:])
clusterAssment[nonzero(clusterAssment[:,0].A==bestCentToSplit)[0],:]=bestClustAss
return centList,clusterAssment
该函数首先创建一个矩阵来存储数据集中的每个点的簇分配结果及平方误差,然后计算整个数据集的质心,并使用一个列表来保留所有的质心。得到上述质心之后,可以遍历数据集中所有点来计算每个点到质心的误差值.这些误差值将会在后面用到。
接下来程序进入while循环,该循环会不停对簇进行划分,知道得到想要的簇数目为止。可以通过考察簇列表的值来获得当前簇的数目。然后遍历所有的簇来决定最佳的簇进行划分。为此需要比较划分前后的SSE。一开始将最小SSE设为无穷,然后遍历簇列表centList中的每一个簇。对每个簇,将该簇中的所有点看成一个小的数据集ptsInCurrCluster。将ptsInCurrCluster输入到函数kMeans()中进行处理(k=2)。 k-均值算法会生成两个(簇),同时给出每个簇的误差值,这些误差与剩余数据集的误差之后作为本次划分的误差,如果该划分的SSE值最小,则本次划分被保存。一旦决定了要划分的簇,接下来执行实际划分操作,只需要将要划分的簇中所有点的簇分配结果进行修改即可。当使用kMeans()函数并制定簇数位2时,会得到两个编号为0和1的结果簇。需要将这些簇编号修改为划分簇及新加簇的编号,该过程可以通过两个数组过滤器来完成,最后,新的簇分配结果被更新,新的质心会被添加到centList中。
当while循环结束时,同kMeans()函数一样,函数返回质心列表和簇分配结果。
下面我们利用一个较难的数据集testSet.txt2来测试二分k-均值算法。
我们可以看到聚类结果比普通k-均值准确很多