十大经典排序算法+Python实现
文章目录
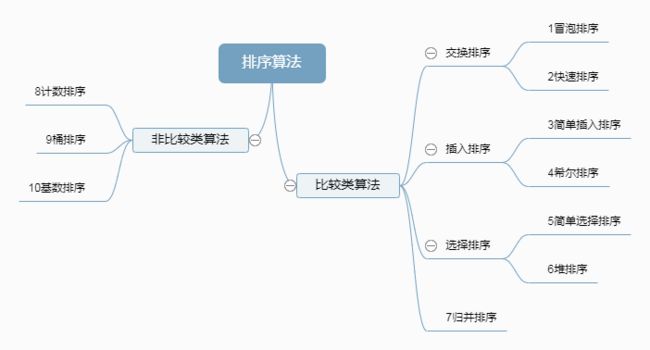
- 0. 算法简述
- 0.1 算法分类
- 0.2 算法复杂度
- 0.3 相关概念
- 0.4 例子说明
- 1. 冒泡排序
- 1.1 简介
- 1.2 算法流程(原理)
- 1.3 算法复杂度分析
- 1.4 算法实现
- 2. 快速排序
- 2.1 简介及算法流程(原理)
- 2.2 算法分析
- 2.3 算法实现
- 3. 插入排序
- 3.1 简介及算法流程(原理)
- 3.2 算法分析
- 3.3 算法实现
- 4. 希尔排序
- 4.1 简介及算法流程(原理)
- 4.2 算法分析
- 4.3 算法实现
- 5. 简单选择排序
- 5.1 简介及算法流程(原理)
- 5.2 算法分析
- 5.3 算法实现
- 6. 堆排序
- 6.1 简介
- 6.2算法流程
- 6.3 算法分析
- 6.4 算法实现
- 7. 归并排序
- 7.1 简介及算法流程(原理)
- 7.2 算法分析
- 7.3 算法实现
- 8. 计数排序
- 8.1 简介
- 8.2 算法(原理)
- 8.2 算法分析
- 8.3 算法实现
- 9. 桶排序
- 9.1 简介及算法流程(原理)
- 9.2 算法分析
- 9.3 算法实现
- 10. 基数排序
- 10.1 简介
- 10.2 算法流程
- 10.3 算法实现
0. 算法简述
0.1 算法分类
这里整理的十种常见排序算法可以分为两大类:
比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
0.2 算法复杂度
上述十种排序算法的算法复杂度如下:
| 排序算法 | 时间复杂度(平均) | (最好) | (最坏) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 1冒泡排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 2快速排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n 2 ) O(n^2) O(n2) | O ( l o g 2 n ) O(log_2n) O(log2n) | 不稳定 |
| 3简单插入排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 4希尔排序 | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 5简单选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 6堆排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( 1 ) O(1) O(1) | 不稳定 |
| 7归并排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n ) O(n) O(n) | 稳定 |
| 8计数排序 | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | 稳定 |
| 9桶排序 | O ( n + k ) O(n+k) O(n+k) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n + k ) O(n+k) O(n+k) | 稳定 |
| 10基数排序 | O ( n ∗ k ) O(n*k) O(n∗k) | O ( n ∗ k ) O(n*k) O(n∗k) | O ( n ∗ k ) O(n*k) O(n∗k) | O ( n + k ) O(n+k) O(n+k) | 稳定 |
0.3 相关概念
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:是一个关于数据规模n的函数,它定性描述了该算法的运行时间。常用大O符号表述,不包括这个函数的低阶项和首项系数。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
0.4 例子说明
下述所有排序算法都基于如下无序序列的测试:
10, 1, 3, 4, 2, 8, 5, 7, 9, 6 #简单无序数列
10, 10, 1, 3, 4, 2, 8, 5, 7, 9 #有重复的数列
1. 冒泡排序
1.1 简介
冒泡排序是因为越大的元素会在排序过程中慢慢“浮”到数列的顶端(升序或降序排列),就像水底的气泡最终会上浮到顶端一样(同时慢慢变大),故名“冒泡排序”(bubble sort)。
1.2 算法流程(原理)
a)、比较相邻的元素。如果第一个比第二个大,就交换他们两个。
b)、对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。这样到最后,当前无序列表中最大的元素会在序列顶端。(因为伴随着交换过程,两个之间大的元素必然更靠近顶端)
c)、针对所有的元素重复以上的步骤,除了最后一个。
d)、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
1.3 算法复杂度分析
a)、若文件的初始状态就是正序的,那么一趟扫描即可完成排序。此时,比较次数为n-1,元素交换次数为0次。所以,冒泡排序最好的时间复杂度为 O ( n ) O(n) O(n) 。
b)、若初始文件是反序的,需要进行(n-1)趟排序。每趟排序要进行(n-i)次关键字的比较(1≤i≤n-1)。在这种情况下,比较次数为 n ∗ ( n − 1 ) 2 \frac{n*(n-1)}{2} 2n∗(n−1),移动次数为 n ∗ ( n − 1 ) 2 \frac{n*(n-1)}{2} 2n∗(n−1),所以冒泡排序的最坏时间复杂度为 O ( n 2 ) O(n^2) O(n2)。平均时间复杂度为: O ( n 2 ) O(n^2) O(n2)
c)、上面的冒泡排序的临时变量所占空间不随处理数据n的大小改变而改变,则空间复杂度为O(1)。
1.4 算法实现
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
#冒泡排序
def bubble_sort(arr):
for i in range(len(arr)):
for j in range(len(arr)-1-i):
if arr[j] - arr[j+1] >= 0:
#如果后一元素大于当前,则交换
arr[j],arr[j+1]=arr[j+1],arr[j]
else:
continue
return arr
print(bubble_sort(original_list))
2. 快速排序
2.1 简介及算法流程(原理)
快速排序(Quicksort)是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1962年提出。
它的基本思想是:先从随机列表中选择一个数作为“主元”,然后通过一趟排序将要排序的数据以“主元”为界限,分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
2.2 算法分析
a)、首先我们要了解,对n维的序列进行划分需要的时间为 Θ ( n ) \Theta(n) Θ(n),对n个元素进行递归操作需要 T ( n ) T(n) T(n)的时间。
b)、那么最坏的情况是,每次选择的主元使得划分的两个部分非常不平衡,即一边一个元素都没有,另外一边有n-1个元素。设该排序运行时间为 T ( n ) T(n) T(n),其中对n维的序列进行划分需要的时间为 Θ ( n ) \Theta(n) Θ(n),那么可以得到递归式: T ( n ) = T ( n − 1 ) + Θ ( n ) T(n)=T(n-1)+\Theta(n) T(n)=T(n−1)+Θ(n),求解过程如下:
| T ( n ) = T ( n − 1 ) + Θ ( n ) T(n)=T(n-1)+\Theta(n) T(n)=T(n−1)+Θ(n) | (1) |
|---|---|
| T ( n ) = ( T ( n − 2 ) + Θ ( n − 1 ) ) + Θ ( n ) T(n)=(T(n-2)+\Theta(n-1))+\Theta(n) T(n)=(T(n−2)+Θ(n−1))+Θ(n) | (2) |
| T ( n ) = T ( n − 2 ) + 2 ∗ Θ ( n ) T(n)=T(n-2)+2*\Theta(n) T(n)=T(n−2)+2∗Θ(n) | 忽略常数项 |
| T ( n ) = T ( n − 3 ) + 3 ∗ Θ ( n ) T(n)=T(n-3)+3*\Theta(n) T(n)=T(n−3)+3∗Θ(n) | (3) |
| … | … |
| T ( n ) = T ( 1 ) + n ∗ Θ ( n ) T(n)=T(1)+n*\Theta(n) T(n)=T(1)+n∗Θ(n) | (n) |
因为: T ( 1 ) = 0 T(1)=0 T(1)=0,常数项
所以: T ( n ) = Θ ( n 2 ) T(n)=\Theta(n^2) T(n)=Θ(n2),即最坏情况的时间复杂度为: O ( n 2 ) O(n^2) O(n2)
c)、最好的情况则是,每次主元划分的两个部分非常均匀,那么可得递推式: T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n)=2T(n/2)+\Theta(n) T(n)=2T(n/2)+Θ(n),求解过程如下:
| T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n)=2T(n/2)+\Theta(n) T(n)=2T(n/2)+Θ(n) | (1) |
|---|---|
| T ( n ) = 2 ( 2 ∗ T ( n / 2 2 ) + Θ ( n / 2 ) ) + Θ ( n ) T(n)=2(2*T(n/2^2)+\Theta(n/2))+\Theta(n) T(n)=2(2∗T(n/22)+Θ(n/2))+Θ(n) | (2) |
| T ( n ) = 2 2 ∗ T ( n / 2 2 ) + Θ ( n ) + Θ ( n ) T(n)=2^2*T(n/2^2)+\Theta(n)+\Theta(n) T(n)=22∗T(n/22)+Θ(n)+Θ(n) | 忽略常数项 |
| T ( n ) = 2 3 ∗ T ( n / 2 3 ) + 3 ∗ Θ ( n ) T(n)=2^3*T(n/2^3)+3*\Theta(n) T(n)=23∗T(n/23)+3∗Θ(n) | (3) |
| … | … |
| T ( n ) = 2 m ∗ T ( 1 ) + m ∗ Θ ( n ) T(n)=2^m*T(1)+m*\Theta(n) T(n)=2m∗T(1)+m∗Θ(n) | (m) |
假设在第m次递归中,n递归至1,则有: n = 2 m n=2^m n=2m,所以 m = l o g 2 n m=log_2n m=log2n。
所以在m步的递归式可写为: T ( n ) = n ∗ T ( 1 ) + l o g 2 n ∗ Θ ( n ) T(n)=n*T(1)+log_2n*\Theta(n) T(n)=n∗T(1)+log2n∗Θ(n)
因为: T ( 1 ) = 0 T(1)=0 T(1)=0
所以: T ( n ) = l o g 2 n ∗ Θ ( n ) T(n)=log_2n*\Theta(n) T(n)=log2n∗Θ(n),即最好情况的时间复杂度为: O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
d)、平均时间复杂度为: O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) (平均复杂度怎么得出来的我一直很疑惑,还不会计算希望大佬赐教一波)
e)、快速排序每次交换时候使用的空间是O(1)的,也就是个常数级;而真正消耗空间的就是递归调用了,因为每次递归就要保持一些数据;最优的情况下空间复杂度为: O ( l o g 2 n ) O(log_2n) O(log2n) ,每一次都平分数组的情况;最差则为 O ( n ) O( n ) O(n),此时退化为冒泡排序的情况。
2.3 算法实现
#快速排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def quick_sort(arr):
#实现递归的话,输入和输出数目要保证一致
if len(arr) >= 2:
base = arr[0] #选取基准值,这里选取了第一个
arr_l = []
arr_r = []
for i in range(1,len(arr)): #第一个值是基准值,从arr[1]开始
if arr[i] - base >= 0:
arr_r.append(arr[i])
else:
arr_l.append(arr[i])
return quick_sort(arr_l) + [base] + quick_sort(arr_r) #递归
else:
return arr
print(quick_sort(original_list))
3. 插入排序
3.1 简介及算法流程(原理)
插入排序法是将序列看成“有序”和“无序两个部分”。基本操作是将一个“无序”序列的一个数据插入到已经排好序的有序数据中,从而得到个数加一的有序数据,和无序数据个数减一的序列。算法时间复杂度为O(n^2),是一种稳定的排序方法。
插入排序的基本思想是:每步将一个待排序的记录,按值的大小依次插入前面已经排序的序列中适当位置上,直到全部插入完为止。
3.2 算法分析
a)、最好的情况,原始序列已经是有序序列。那么对于n个数据的序列,只需要进行(n-1)次比较就可以完成排序(第一个数据默认为有序序列),因此最好情况的时间复杂度为O(n)。
b)、最坏的情况,原始序列为反序。那么对于n个数据的序列(第一个序列默认为有序)。
在第一次插入时,需要与前面有序序列进行1次比较,此时有序序列变成2,无需序列变成n-2;在第二次插入操作时,第三个数需要与前面2个数据进行比较,有序序列变成3,无序为n-3;…那么在第n-1次操作时(即对最后一个无序序列数据进行插入操作时),需要与前面n-1个数据进行对比,然后插入在第一个位置。综上,一共经过n*(n-1)/2次比较,取最高项,可得时间复杂度为:O(n^2)。
c)、对于平均的情况,可以想象就是每次的比较次数在最坏情况的一般,那么总次数就会比最坏情况少了一半。然而,时间复杂度的度量不关心系数,因此插入排序的平均时间复杂度为O(n^2)。
d)、插入排序每次比较时从无序列表中取待比较的数据,因此空间是O(1)。
3.3 算法实现
#简单插入排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def insection_sort(arr):
for i in range(1,len(arr)): #默认第一个元素已经在有序列表中
for j in range(i,0,-1): #将arr[i]与有序列表中的元素比较
if arr[j-1] - arr[j] >= 0:
arr[j-1],arr[j] = arr[j],arr[j-1]
return arr
print(insection_sort(original_list))
4. 希尔排序
4.1 简介及算法流程(原理)
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
希尔排序是把记录按一定的步长分组(例如,数据长度为10,假设初始步长为5,那么序列(1,6),(2,7),(3,8)…各为一组),对每组使用直接插入排序算法排序;接着在下一次操作是减少步长,那么每组包含的数据越来越多,当步长减至1时,整个文件恰被分成一组,算法也便终止。
4.2 算法分析
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,插入排序的元素个数很少,所以此时用插排速度很快;到后面步长比较小的时候,元素也基本有序了,插入排序效率也很高了。所以,希尔排序的时间复杂度会比o(n^2)好一些。
a)、最好情况,同插排,已经有序序列。那么当步长直接为1,也就和插排一样了,只需要n-1次比较。因此,最好情况时间复杂度为O(n)。
b)、最坏情况,反序。时间复杂度为O(n^2)。----------------(暂不会解释)
c)、这里关于平均时间复杂度的说法,转自百度百科:Shell排序的执行时间依赖于增量序列。好的增量序列的共同特征:① 最后一个增量必须为1;② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。有人通过大量的实验,给出了较好的结果:当n较大时,比较和移动的次数约在n^ l.25 到 n^ 1.6之间。
d)、关于空间复杂度,shell排序,每次操作也只需要储存待比较数据,O(1)。
4.3 算法实现
#4希尔排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def shell_sort(arr):
step = len(arr)//2
while step > 0:
for i in range(0, step):
for j in range(i+step,len(arr),step):
for k in range(j,0,-step):
if arr[k-step] - arr[k] >= 0:
arr[k-step],arr[k] = arr[k],arr[k-step]
step = step//2
return arr
print(shell_sort(original_list))
5. 简单选择排序
5.1 简介及算法流程(原理)
选择排序(Selection sort),是我们凭直觉最容易想到的排序方式。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法。
5.2 算法分析
a)、对于选择排序,无论是如何的原序列,每次从无序序列中选择当前最小(或最大)的一个元素时,都要与其他元素比较一次。因此,最好,最差,平均时间复杂度均为O(n)。
b)、选择排序时,每次操作只需要占用一个空间位置来储存当前的最小(或最大)的元素,因此空间复杂度为O(1)。
5.3 算法实现
#简单选择排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def slect_sort(arr):
for i in range(len(arr)-1):
for j in range(i+1,len(arr)): #将当前数与其余数进行比较
if arr[i] > arr[j]:
arr[i], arr[j] = arr[j], arr[i]
return arr
print(slect_sort(original_list))
6. 堆排序
6.1 简介
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。
首先解释一波什么是“堆结构”。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
6.2算法流程
首先根据堆的定义,将原数组调整为初始的最大堆:将堆的末端子节点作调整,使得子节点永远小于父节点。然后,基于当前堆,交换位在堆顶第一个数据(即最大数据)与堆末端最右的数据(交换后,最后一个为最大值,将其视为有序,后续堆操作不将其计入操作范围),对无序区重新做最大堆调整。将上述过程做递归运算。直到最后无序区只剩一个元素。此时排序可视为完成。
因为对于堆而言,对顶定为当前最大(如有相等情况,堆顶也是最大),每次相当于将最大的挑选出来放入有序列表中。依次操作,完成排序。
6.3 算法分析
堆排序分为两个部分,第一个部分是初始大顶堆的构造部分。第二部分是递推过程中改善堆的部分。
a)、对于第一部分,时间复杂度为O(n)--------(这里我不是很理解,就不写上来原因了)
第二部分为O(nlogn),因为每次循环改善堆的过程都会经过logn次比较(这里的logn指堆的深度),因此,对于n个元素,要经过n次循环。时间复杂度为O(nlogn)。
b)、空间复杂度为O(1),因为堆排序为原址排序,比较式占用常数空间,无序额外占用空间。
6.4 算法实现
#堆排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def heap_sort(arr):
'''构造大顶堆的函数 arr为输入的无序序列 start为需要操作的开始序号 end为序列最后的子节点序号 '''
def big_endian(arr, start, end):
while True: #每次对进来的序数进行重新排序
num = 2*start + 1 #子节点的序号(左边)
if num > end: #当前序号如果大于end序号,则大顶堆构造完成
break
if num + 1 <= end and arr[num] < arr[num+1]:
num += 1 #保证父节点都与子节点中较大的进行比较
if arr[start] < arr[num]:
arr[start], arr[num] = arr[num],arr[start]
start = num #如果父子节点发生互换,则继续检查下一级节点
else:
break #如果父节点与子节点没有发生互换,则直接退出
first = len(arr)//2 - 1 #首先构建大顶堆,保证父节点大于子节点的完全二叉树
for start in range(first,-1,-1): #从下至上,初始大顶堆
big_endian(arr,start,len(arr)-1)
for n in range(len(arr)-1, 0, -1): #再从上而下进行构造
arr[0],arr[n] = arr[n],arr[0] #每次将堆顶元素(当前最大值)与最后元素对换
big_endian(arr,0,n-1)
return arr
print(heap_sort(original_list))
7. 归并排序
7.1 简介及算法流程(原理)
归并排序是一个典型的基于分治的递归算法。它不断地将原数组分成大小相等的两个子数组(奇数序列的话,可能相差1),最终当划分的子数组大小为1时。再进行归并操作,将划分子序列有序组合并成一个更大的有序数组。最终返回的数组为元序列的有序版本。
7.2 算法分析
a)、假设排序一个n个元素的数组需要花费T(n)时间,那么T(n)来自于分治模式的三个部分所耗时间的累加和:
1)、对于“分”的阶段,每次分解只计算了长度length的一半这个一次操作θ(1)。
2)、每个子数组有n/2个元素,一次每个数组递归调用花费了T(n/2)时间。
3)、合并阶段,合并排序中将两个数组长度和为n的数组排序需要花费的时间为θ(n)的时间。
步骤1,3,只保留高阶项,因此共花费时间为θ(n)。
因此,可得递归式:T(n)=2*T(n/2)+θ(n)。 这个递归式求解方式与前述快速排序 的推导一样,因此归并排序的时间复杂度为:O(nlog2n)。
对于归并排序,最好最坏平均的时间复杂度均经过上述过程,因此时间复杂度均为O(nlog2n)
b)、归并排序不是原址排序,对大的空间发生在最后一次“并”操作,输入的left和right是对原数组进行拷贝的两个子数组,长度和为n。因此,归并操作的空间复杂度为O(n)。
7.3 算法实现
#归并排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def merge_sort(arr):
def merge_part(left,right): #并的阶段
i,j = 0,0
new_arr = []
while True:
if i >= len(left): #左边序列索引结束,就将右边剩余加到列表
new_arr.extend(right[j::])
break
elif j >= len(right): #右边序列索引结束,就将左边剩余加到列表
new_arr.extend(left[i::])
break
if left[i] >= right[j]: #比较左右列表中元素,将小的放入新列表中
new_arr.append(right[j])
j += 1
else:
new_arr.append(left[i])
i += 1
return new_arr
if len(arr) <=1:
return arr
length = len(arr) // 2
left = merge_sort(arr[:length]) #递归分治阶段
right = merge_sort(arr[length:]) #递归分治阶段
return merge_part(left,right) #每次返回合并后的新列表
print(merge_sort(original_list))
8. 计数排序
8.1 简介
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。但是,计数排序的局限也在这里,这是一种牺牲空间换取时间的做法,而且当O(k)>O(n*log(n))的时候其效率反而不如一些比较排序。此外,计数排序需要输入数据为整数,有限的序列。
8.2 算法(原理)
假设输入的线性表L的长度为n,L=L1,L2,…,Ln;线性表的元素属于有限偏序集S,且|S|=k,在这里的k是非重复元素的个数。(这里k的描述,不同于百度百科:k=O(n)。但是cd觉得表示为非重复元素的个数更合适。包括以下算法流程及实现,cd都是将k理解为序列非重复元素个数)
8.2 算法分析
a)、时间复杂度,在各个情况下均为O(n+k)。----------(cd不确定就不展开解释了)
b)、空间复杂度,为新序列消耗空间n,加上集合消耗空间k。空间复杂度为O(n+k)。
8.3 算法实现
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
#计数排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def cont_sort(arr):
arr_ele = list(set(arr)) #数列中不同元素共k个,空间复杂度k
arr_cont = {} #用来计数的字典,这空间消耗跟写法有关,可以归到arr_ele去
arr_new = [None]*len(arr) #开辟空间存储新的数列,空闲复杂度n
for i in arr_ele: #对每个元素计数,累计数列中不大于其的个数
p = 0
for j in range(len(arr)):
if i >= arr[j]:
p += 1
arr_cont[i] = p #累计数列中不大于当前数的个数
for k in arr: #range是开区间,正好抵消了将自己计数的一次
arr_new[arr_cont[k]-1] = k #python计数是从0开始的
arr_cont[k] = arr_cont[k]-1 #如果有重复数字,则下次排在前面
return arr_new
print(cont_sort(original_list))
9. 桶排序
9.1 简介及算法流程(原理)
桶排序,是基于分治法的思想整出来的一个算法。桶排序假设待排序的一组数均匀独立的分布在一个范围中,并将这一范围划分成几个子范围(桶)。然后在各个桶里将数据排序好(各个桶里排序可以用各种比较类排序都行)。接着依次取出各个桶里的子序列拼接在一起则形成了有序的序列。(这里设立桶的时候,桶的大小范围是实现确定的。)
9.2 算法分析
a)、最好情况是当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n))。对于n个待排数据,m个桶,平均每个桶[n/m]个数据的桶排序平均时间复杂度为:O(n)+O(m* (n/m)* log(n/m))=O(n+n* (logn-logm))=O(n+nlogn-nlogm)=O(n)。
式中起始的O(n)表示为将序列放进各个桶的时间消耗。当N=M时,即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。
因此,桶排序的平均时间复杂度为线性的O(N+k),其中k=N*(logN-logM)。如果相对于同样的N,桶数量M越大,其效率越高,最好的时间复杂度达到O(N)。当然桶排序的空间复杂度为O(N+M),如果输入数据非常庞大,而桶的数量也非常多,则空间代价无疑是昂贵的。此外,桶排序是稳定的。
b)、空间复杂度方面,桶排序额外开辟了空间用于将原数列分配。因此,空间复杂度为O(n+k),其中k与桶的数量有关。
9.3 算法实现
#桶排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def bucket_sort(arr):
''' 桶排序在处理大数据量的时候比较有优势,有分而治之的思想 '''
#首先求出数列的最大最小值,确定桶的范围,通常是已知的
max_n, min_n = max(arr), min(arr)
bucket_num = len(arr)//3 #桶的数量定的方式很多,这里定了3个
boundary = (max_n - min_n)/(bucket_num-1) #每个桶的范围
#创建空桶,这里用字典来表示
bucket={}
for i in range(bucket_num):
bucket[i]=[]
#然后遍历一遍将所有元素放入各个桶中
for j in range(len(arr)):
num = (arr[j]-min_n) // boundary
bucket[num].append(arr[j])
#对各个桶中的数据进行排序,可以用任何一种排序。这里用自带的sort排序(这个倒不是的重点)
#然后按照序号依次将桶中数据输出
arr_new = []
for k in range(bucket_num):
bucket[k].sort()
arr_new.extend(bucket[k])
return arr_new
print(bucket_sort(original_list))
10. 基数排序
10.1 简介
基数排序(radix sort),是透过键值的部份资讯,将要排序的元素分配按照规则排列到某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog®m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。(只能对整数序列排序)
10.2 算法流程
首先根据个位数的数值,在走访数值时将它们分配至编号0到9的桶子中,接下来将这些桶子中的数值重依次回收串接起来;
接着再进行一次分配,这次是根据十位数来分配至编号0到9的桶子中,然后再依次回收;
…(指导序列中最大数的最高位分配完毕)
接下来将最后一次桶子中的数值重新依次串接起来,便是最终排序完成的序列。
10.3 算法实现
#基数排序
original_list=[10, 1, 3, 4, 2, 8, 5, 7, 9, 6]
#original_list=[10, 10, 1, 3, 4, 2, 8, 5, 7, 9]
def radix_sort(arr):
import math
radix = 10
num = int(math.ceil(math.log(max(arr)+1,radix))) #加1因为,10这样的算两位
#创建radix个空桶
bucket = [[] for i in range(radix)] # 不能用 [[]]*radix
for i in range(1,num+1): #进行num次循环
for j in range(len(arr)): #放入桶中
bucket[arr[j]%(radix**i)//(radix**(i-1))].append(arr[j])
arr_new = []
for k in range(radix): #合并桶按照从小到大
arr_new.extend(bucket[k])
arr = arr_new[:]
bucket = [[] for i in range(radix)] #初始化bucket
return arr
print(radix_sort(original_list))