机器学习西瓜书（周志华）第六章 支持向量机（SVM）

1. 概述

       支持向量机（support vector machines, SVM）是一种二分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；支持向量机还包括核技巧，这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题，支持向量机的学习算法是求解凸二次规划的最优化算法。
支持向量机学习方法包含构建由简至繁的模型：

• 线性可分支持向量机——硬间隔支持向量机（硬间隔最大化）——训练数据线性可分
• 线性支持向量机——软间隔支持向量机（软间隔最大化）——训练数据近似线性可分
• 非线性支持向量机——核技巧及软间隔最大化——训练数据线性不可分

核方法是比支持向量机更为一般的机器学习方法。

2. 感知机

       感知机的模型就是尝试找到一条直线，能够把二元数据隔离开。放到三维空间或者更高维的空间，感知机的模型就是尝试找到一个超平面，能够把所有的二元类别隔离开。对于这个分离的超平面，定义为$w^{T}x+b=0$，如下图。在超平面$w^{T}x+b=0$上方的我们定义为y=1,在超平面$w^{T}x+b=0$下方的我们定义为y=−1。可以看出满足这个条件的超平面并不止一个。如何判断哪个超平面的分类效果更好。

接着我们看感知机模型的损失函数优化，它的思想是让所有误分类的点(定义为M)到超平面的距离和最小，即最小化下式：
$$\sum _{x_i\in M}\frac{-y_i(w^T{x}_i+b)}{||w|{|}_2}$$
　　　　当w和b成比例的增加，比如,当分子的w和b扩大N倍时，分母的L2范数也会扩大N倍。在感知机模型中，我们采用的是保留分子，固定分母$||w|{|}_2=1$,即最终感知机模型的损失函数为：
$$\sum _{x_i\in M}-y_i(w^T{x}_i+b)$$
　　　　如果我们不是固定分母，改为固定分子，作为分类模型有没有改进呢？
这些问题在SVM会详细解释。

3. 间隔与支持向量

3.1 间隔

      函数间隔是没有统一量度，没有规范化，并不能正常反应点到超平面的距离，在感知机模型里，当分子成比例的增长时，分母也是成倍增长。为了统一度量，需要对法向量w加上约束条件，这样就得到了几何间隔 $\gamma$,定义为：
$$\gamma =\frac{y(w^{T}x+b)}{||w|{|}_2}=\frac{\gamma \prime }{||w|{|}_2}$$
      几何间隔才是点到超平面的真正距离，感知机模型里用到的距离就是几何距离。

3.2 支持向量

       在感知机模型中，可以找到多个可以分类的超平面将数据分开，并且优化时希望所有的点都离超平面远。但是实际上离超平面很远的点已经被正确分类，让它离超平面更远并没有意义。反最关心是那些离超平面很近的点，这些点很容易被误分类。如果可以让离超平面比较近的点尽可能的远离超平面，那分类效果会好有一些。SVM的思想起源正起于此。

       如下图所示，分离超平面为 $w^{T}x+b=0$，如果所有的样本不光可以被超平面分开，还和超平面保持一定的函数距离（下图函数距离为1），那么这样的分类超平面是比感知机的分类超平面优的。可以证明，这样的超平面只有一个。和超平面平行的保持一定的函数距离的这两个超平面对应的向量，我们定义为支持向量，如下图虚线所示。

4. SVM模型目标函数与优化

       SVM的模型是让所有点到超平面的距离大于一定的距离，也就是所有的分类点要在各自类别的支持向量两边。用数学式子表示为：

$$\max \frac{2}{||w||}s.t{y}_i(w^T{x}_i+b)\ge 1(i=1,2,...m)$$

由于$\frac{2}{||w||}$的最大化等同于$\frac{||w|{|}^2}{2}$的最小化。这样SVM的优化函数等价于：

$$\min \frac{||w|{|}^2}{2}s.t{y}_i(w^T{x}_i+b)\ge 1(i=1,2,...m)$$

由于目标函数$\frac{||w|{|}^2}{2}$是凸函数，同时约束条件不等式是仿射的，根据凸优化理论，可以通过拉格朗日函数将我们的优化目标转化为无约束的优化函数，这和最大熵模型原理小结中讲到了目标函数的优化方法一样。具体的，优化函数转化为：

$$L(w,b,\alpha )=\frac{||w|{|}^2}{2}+\sum _{i=1}^m(1-{\alpha }_i[y_i(w^T{x}_i+b)])满足{\alpha }_i\ge 0$$

可以先求优化函数对于w和b的极小值。接着再求拉格朗日乘子$\alpha$ 的极大值。

       首先来求$L(w,b,\alpha )$基于w 和 b 的极小值，即$mi{n}_{w,b}L(w,b,\alpha )$。这个极值我们可以通过对w和b分别求偏导数得到：
$$\frac{\partial L}{\partial w}=0\Rightarrow w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i$$
$$\frac{\partial L}{\partial b}=0\Rightarrow \sum _{i=1}^m{\alpha }_i{y}_i=0$$

       现在我们来看将w替换为$\alpha$的表达式以后的优化函数$\psi (\alpha )$的表达式：

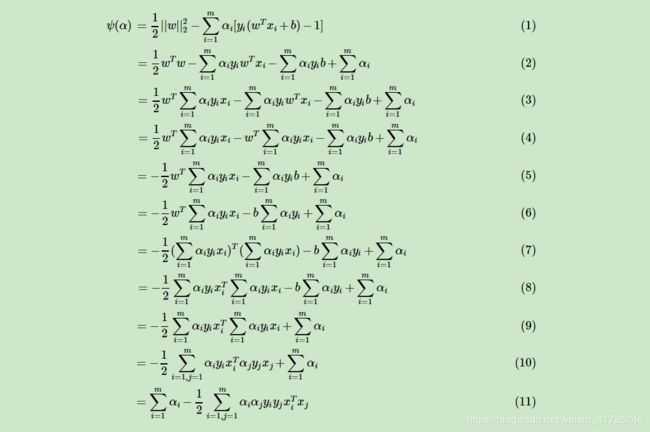
5. 线性可分支持向量机的算法过程

      这里我们对线性可分SVM的算法过程做一个总结。

      输入是线性可分的m个样本$(x_1,y_1),(x_2,y_2),...,(x_m,y_m),$,其中x为n维特征向量。y为二元输出，值为1，或者-1。

      输出是分离超平面的参数$w^{\ast }$和$b^{\ast }$和分类决策函数。

      算法过程如下：

1）构造约束优化问题
$$mi{n}_{\alpha }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\bullet x_j)-\sum _{i=1}^m{\alpha }_i$$
$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$
$${\alpha }_i\ge 0i=1,2,...m$$
2）用SMO算法求出上式最小时对应的α向量的值${\alpha }^{\ast }$向量.

3 ) 计算$w^{\ast }={\sum }_{i=1}^m{\alpha }_i^{\ast }{y}_i{x}_i$
4 ) 找出所有的S个支持向量,即满足${\alpha }_s>0$对应的样本$(x_s,y_s)$，
      通过 $y_s({\sum }_{i=1}^m{\alpha }_i{y}_i{x}_i^T{x}_s+b)=1$，
      计算出每个支持向量$(x_s,y_s)$对应的$b_s^{\ast }$,
      计算出这些$b_s^{\ast }=y_s-{\sum }_{i=1}^s{\alpha }_i{y}_i{x}_i^T{x}_s$.
      所有的b∗s对应的平均值即为最终的$b^{\ast }=\frac{1}{S}{\sum }_{s=1}^S{b}_s^{\ast }$
       这样最终的分类超平面为：$w^{\ast }\bullet x+b^{\ast }=0$，
       最终的分类决策函数为： $f(x)=sign(w^{\ast }\bullet x+b^{\ast })$

       线性可分SVM的学习方法对于非线性的数据集是没有办法使用的， 有时候不能线性可分的原因是线性数据集里面多了少量的异常点，由于这些异常点导致了数据集不能线性可分， 那么怎么可以处理这些异常点使数据集依然可以用线性可分的思想呢？ 我们在下一节的线性SVM的软间隔最大化里继续讲。

6. 线性支持向量机

      现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分；退一步讲，即便恰好找到某个核函数使得训练样本在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。缓解该问题的一个方法是允许支持向量机在一些样本上出错。为此引入“软间隔”概念。

      所谓的软间隔，是相对于硬间隔说的，我们可以认为上一篇线性分类SVM的学习方法属于硬间隔最大化。

      回顾下硬间隔最大化的条件：
$$\min \frac{||w|{|}^2}{2}s.t{y}_i(w^T{x}_i+b)\ge 1(i=1,2,...m)$$
$$L(w,b,\alpha )=\frac{||w|{|}^2}{2}+\sum _{i=1}^m(1-{\alpha }_i[y_i(w^T{x}_i+b)])满足{\alpha }_i\ge 0$$
接着我们再看如何可以软间隔最大化呢？

      SVM对训练集里面的每个样本$(x_i,y_i)$引入了一个松弛变量${\xi }_i\ge 0$,使函数间隔加上松弛变量大于等于1，也就是说：
$$y_i(w^T\bullet x_i+b)\ge 1-{\xi }_i$$
      对比硬间隔最大化，可以看到我们对样本到超平面的函数距离的要求放松了，之前是一定要大于等于1，现在只需要加上一个大于等于0的松弛变量能大于等于1就可以了。当然，松弛变量不能白加，这是有成本的，每一个松弛变量${\xi }_i$, 对应了一个代价${\xi }_i$，这个就得到了我们的软间隔最大化的SVM学习条件如下：
$$min\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m{\xi }_i$$
$$s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i(i=1,2,...m)$$
$${\xi }_i\ge 0(i=1,2,...m)$$
      这里，C>0为惩罚参数，可以理解为我们一般回归和分类问题正则化时候的参数。C越大，对误分类的惩罚越大，C越小，对误分类的惩罚越小。
也就是说，我们希望$\frac{1}{2}||w|{|}_2^2$尽量小，误分类的点尽可能的少。C是协调两者关系的正则化惩罚系数。在实际应用中，需要调参来选择。

6.1 线性支持向量机的软间隔最大化目标函数的优化

可以利用上面的三个式子去消除w和b了。

6.2 软间隔最大化时的支持向量

      在硬间隔最大化时，支持向量比较简单，就是满足$y_i(w^T{x}_i+b)-1=0$就可以了。根据KKT条件中的对偶互补条件${\alpha }_i^{\ast }(y_i(w^T{x}_i+b)-1)=0$，如果${\alpha }_i^{\ast }>0$则有$y_i(w^T{x}_i+b)=1$即点在支持向量上，否则如果${\alpha }_i^{\ast }=0$则有$y_i(w^T{x}_i+b)\ge 1$，即样本在支持向量上或者已经被正确分类。

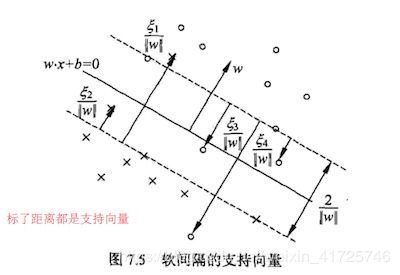
      在软间隔最大化时，则稍微复杂一些，因为我们对每个样本$(x_i,y_i)$引入了松弛变量${\xi }_i$。我们从下图来研究软间隔最大化时支持向量的情况，第i个点到对应类别支持向量的距离为${\xi }_i||w|{|}_2$。根据软间隔最大化时KKT条件中的对偶互补条件${\alpha }_i^{\ast }(y_i(w^T{x}_i+b)-1+{\xi }_i^{\ast })=0$我们有：

      a) 如果α=0,那么$y_i(w^T{x}_i+b)-1\ge 0$,即样本在间隔边界上或者已经被正确分类。如图中所有远离间隔边界的点。

      b) 如果0<α${\xi }_i=0,y_i(w^T{x}_i+b)-1=0$,即点在间隔边界上。

      c) 如果α=C，说明这是一个可能比较异常的点，需要检查此时ξi
　　　      i)如果$0\le {\xi }_i\le 1$,那么点被正确分类，但是却在超平面和自己类别的间隔边界之间。如图中的样本2和4.

      　　　ii)如果${\xi }_i=1$,那么点在分离超平面上，无法被正确分类。

      　　　iii)如果${\xi }_i>1$,那么点在超平面的另一侧，也就是说，这个点不能被正常分类。如图中的样本1和3.

6.2 软间隔最大化的线性支持向量机的算法过程

公式参考: [https://blog.csdn.net/weixin_41725746/article/details/90483885#3_457]

7. 课后练习参考答案

[https://blog.csdn.net/icefire_tyh/article/details/52065224]

参考文献：
[1] [统计学习-李航]
[2] [机器学习西瓜书-周志华]
[3] [https://www.cnblogs.com/pinard/p/6103615.html]