数据结构与算法面试知识点汇总（超全）
文章目录
- 一、哈希函数和哈希表
- 01 哈希函数
- 02 哈希表
- 二、布隆过滤器
- 三、一致性哈希
- 四、并查集
- 01 具体实现
- 02 优化
- 03 代码实现
- 五、前缀树（trie树）
- 六、B树和B+树
- 七、线段树
- 01 线段树的优势
- 02 线段树实现
一、哈希函数和哈希表
01 哈希函数
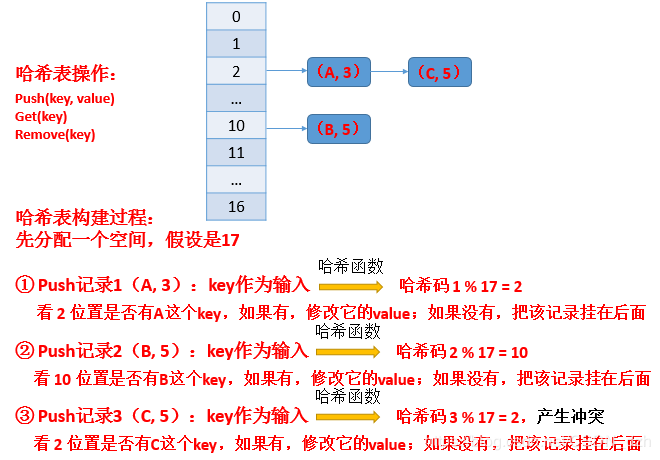
哈希函数（散列函数）：类似于函数调用一样，给一个字符串作为输入，返回一个哈希码。
哈希表（散列表）：把哈希码映射到表中的一个位置来访问记录，存放记录的数组就叫散列表
- 直接寻址法：hash（key） = a * key + b
- 数字分析法
- 平方取中法
- 折叠法
- 随机数法
- 除留余数法
性质：
1）输入域是无穷大的
2）输出域是有穷的，输出域要比输入域小
3）哈希函数不是一个随机函数，只要输入一样，输出就一样
4）输入域这么大而输出域这么小，而由于特性3的关系，就会导致输入不一样也有可能得到输出一样的值（哈希碰撞）
5）虽然有哈希碰撞，如果输入够多，将在整个输出域上均匀地出现返回值，不一定完全平分，但输出域中的每个哈希码一定被差不多个输入域中的值对应
6）因为要做到均匀分布，于是哈希函数跟输入的规律是没有关系的，可以打乱输入规律
推广：
当输入域足够大，经过一个哈希函数计算完后保证输出域是均匀分布时，
对输出域的每一个哈希码模%上一个m，最终的域会缩减成0至m-1，也均匀分布
工程应用：
如何找到1k个相对独立的哈希函数，一个哈希函数的规律跟另一个哈希函数的规律是无关的
只要用1个哈希函数就能改出1k个来，如：哈希f1 + k * 哈希f2 = 哈希fn
02 哈希表
实现原理：
解决哈希冲突（key1和key2称为同义词）的方法：
- 开放寻址法（包括线性探测再散列、二次探测再散列（改善堆积现象）、伪随机探测再散列、双散列法），容易造成堆积现象
- 链地址法：在原地址新建一个空间，以链表结点的形式插入到该空间。链地址算法的基本思想是将所有哈希地址为 i 的元素构成一个称为同义词链的单链表，并将单链表的头指针存在哈希表的第i个单元中，因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。插入新数据项的时间随
装载因子线性增长。
哈希表扩容：
如果发现某个位置上的链的长度到达k了，那么可以认为其它位置上链的长度也到达k了。此时，可能下一次加记录的话效率就不行了，这时就要经历哈希表的扩容
- 首先要将原来的哈希域（如前面的17），扩展到104（或别的）。
- 扩完之后如果要模104，则原来的记录都会失效。此时要将每一个记录都拿出来，用哈希函数计算完之后去模上104，再分配其在哪个位置。
那么，扩容代价不用计算吗？为什么能做到O(1)呢？
一方面样本量是N，若每次扩容都让哈希域长度增加k倍，则扩容平均代价是O（logkN）可很低
另一方面还可以离线扩容。
于是哈希表的增删改查是O（1）的。
Q：有一个大文件100T，每一行是一个字符串，是无序的，让你打印重复的字符串
A：如果单核单CPU单台机器去搞这个事情，那头都大了
Q：说得对，那你怎么办？
A：这是一个大数据问题，可以通过哈希来分流，你给我多少台机器呢？大文件存在哪呢？
Q：给你1000台机器干这个事情，大文件存在一个分布式文件系统上，按行读有很快的工具
A：
- 1）首先对机器标号0-999，把每一行作为一个文本读出来，
利用哈希函数去算一个哈希码，去模1000，
当然也不一定要你提供的1k台机器，只要我能知道里面有m种字符串就好了，就模m- 2）然后将结果放到对应标号的机器中，用一个文件记录下来。
这样就把这个大文件分到了m台机器上去，而且相同的重复文本一定会分配到同一台机器上（哈希函数的性质：相同输入相同输出，不同输入均匀分布）- 3）然后在单台机器上去统计有哪些重复的，最后就是1k台机器并发
如果单台机器上的文件还是太大，再在这个机器上做相同的步骤，在单台机器上并行计算即可
二、布隆过滤器
主要用于解决爬虫去重问题以及黑名单问题，其短板是它有失误率。
这个失误是指：宁可错杀，绝不放过1个的类型。如果是坏人，一定报警。如果是好人，也可能报警，但几率较小
以黑名单问题来举例：
有这么个需求，100亿个URL是黑名单，假设每个URL是64字节，
当用户想搜索某个URL时，如果它是黑名单里的URL，就要对它进行过滤
解决方案：
1）首先它可以通过哈希表实现，但是需要多少个空间呢？
- 由于这里面不用存value，只用存key，于是它是一个hashSet，key是URL字符串
- 这里起码需要6400亿个字节才能把这些URL装下，还不算指针、索引等所占的空间，实际上是比6400亿字节（640G）大的， 如果做成哈希表全放内存中，代价是很高的，而且服务器还要用分布式内存
- 这个设计就耗费了巨大的代价。即便用哈希函数分流到多个机器上，这浪费了机器
2）那怎么能仅适用一台机器就能提供服务呢？——布隆过滤器
- 在哈希来哈希去的经典方法说了以后，应该问允许有很低的失误率吗？——允许。这个时候就可以使用布隆过滤器。它是一个bit类型的map。
实现方法：
第一步：
准备一个数组，从0到m-1位置，每个位置上不是整数也不是串，是一个bit，只有两种状态0/1
int *arr = new int[1000]; // 分配4*1000字节的连续内存，共4*1000*8个bit
这样，就用基础类型int做出了一个0到m-1长度为m的bit类型的数组。如果想省空间，就用long类型，8个字节64位。此外还能做成矩阵的形式。
如果想让第300000个bit位置置1，此时int index = 300000，
- ① 定位这个bit来自于哪个桶
int intIndex = index / 32;- ② 定位这个位置来自于这个桶的哪个bit位
int bitIndex = index % 32;- ③
arr[intIndex] = (arr[intIndex] | (1 << bitIndex));第二步：
有了这个数组以后，
- ① 将黑名单内的所有URL，
输入k个相互独立的哈希函数中，得到k个哈希码，分别取模上m，算出来的对应数组中的那个位置1。若产生哈希碰撞，不管，还是置1。这个过程结束以后，URL进入布隆过滤器。注意：这个数组应当长一些，如果太短，则很容易每个位置都变成1，这样用户输入的URL就全都是黑名单了。- ② 查URL的过程：将用户提供的URL，也做步骤①，如果算出来的k个位置都已经置1，则说这个URL在黑名单中。如果仅有一个甚至几个没被置1，说明这个URL不在黑名单中（
哈希函数特性：相同输入一定有相同输出）。失误的时候就出现在数组开的比较小。- 通过调整数组的大小m和哈希函数的个数k，可以得到不同的失误率。
三、一致性哈希
经典服务器抗压结构：
比如提供一个根据用户QQ号（key）返回其网龄（value）的服务。如何使其负载均衡呢？
- 首先会有一个前端（Nginx），用于接受请求，请求可以发送到任意一个前端上，提供的服务相同
- 然后有一个后端集群组，假设有3台机器m1，m2，m3
- 首先信息会发送到前端上，经前端的同样一份哈希函数算出哈希码，模上3得到对应的机器，将这个信息存到对应的机器中。如果数据足够多，数据是均匀地存在三台机器中的，
负载均衡：每台机器处理的东西是差不多的，CPU占用差不多，内存使用差不多，相关系统性能指标差不多。- 在查的时候，依然是经过上面的步骤，由于相同输入一定导致相同输出，就会到相应的机器上去拿出这个记录，返回给前端，然后前端返回给用户。
上面提到的经典服务器有什么问题呢？——当增加机器或减少机器时，它就炸了
原因：
这和哈希表扩容是一样的，如果加机器加到100，原来模的是3，现在要模100，所有的数据归属全变了。所以必须要把原来的记录都拿出来再算一次，然后迁移到相应的机器上。代价很高
于是有了一致性哈希结构，可实现把原来全部数据迁移的代价变得很低，并负载均衡。
具体是这样的：
那么如何实现它呢？
- 对于后端——还是那三台机器
- 对于前端——还是无差别的负载的服务器
然后，
对三台机器对应的哈希值排好序之后做成一个数组，存到前端中去。
这样，不管请求发送到前端的哪一个机器上，由于每个机器上都有这么一个数组，二分的方式找到第一个大于等于算出来的哈希值的那个位置，就知道这个请求应当由哪个机器处理了。
即便你有10亿台机器，由于采用二分的方法，log以后复杂度也是很低的。
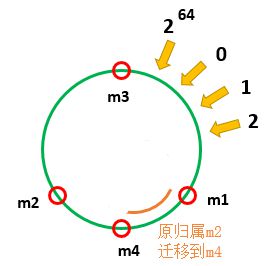
那为什么说它克服了传统服务器结构中加减机器的问题呢？
比如加了一台m4，同样也映射到环上。
这样，
- 在增加机器时，不需要去迁移m1和m3全部的数据，只用迁移原本属于m2的数据即可完成
- 在减少机器时，只需要把m4的数据迁移到m3上即可
于是，这种结构，加减机器数据迁移的代价是非常低的
但是，存在什么问题呢？
- 在机器数量比较少时，这个环是不能够保证其均分的（哈希函数的性质：量在多的时候，才是均匀分布的）。这样负载就会出现问题，一台机器很忙，一台机器却闲得发慌
- 即便可以保证均匀，在加一个机器之后负载就不均了
把上述两个问题解决了，一致性哈希就能既做到数据迁移的代价小，又能保证负载均衡。
虚拟结点技术：
- 真实机器m1，给它分配1k个虚拟结点
- m2，m3也同样都分配1k个虚拟结点
此时，不让m1，m2，m3各自的ip去映射到环上，
准备一张路由表，这个路由表可以由真实机器去查它有哪些虚拟结点，同样也可以由虚拟结点去查它属于哪个真实机器- 让这3k个虚拟结点经哈希函数映射到环上，某个虚拟结点负责的域均给它的真实机器处理
3k个虚拟结点占据了这个环，于是三台机器负责的数据就是差不多的了，负载均衡！如果此时增加一台机器m4，让它也分配1k个虚拟结点，让它们直接进环，再做数据迁移即可
拿走的数据（由m1、m2、m3的部分数据组成）是由虚拟结点决定的。
虚拟结点导致的哈希冲突：冲冲呗，碰撞的概率很小，两个机器共同存一份。
四、并查集
解决的是
- 1）非常快地检查两个元素各自所在的集合是否属于一个集合。
- 2）两个元素各自所在的集合，合并在一块
例子：有元素A，元素B，其中A∈集合set1，B∈集合set2
- 对于1），有函数
isSameSet(A, B)，用于查set1和set2是否一个集合。- 对于2），有函数
union(A, B)，用于set1和set2合并。那么可以怎么实现呢？
- 方案1：
使用链表list，把每个集合当做一个list，每个元素是一个node，放在list中
对isSameSet而言，可以遍历list1，看其中有没有B（缺点是需要遍历，慢）
对union而言，就把两个list接起来即可- 方案2：
使用哈希表set，把每个集合当做一个set，每个元素是一个node，放在set中
对isSameSet而言，可以再set1中以O（1）去查有没有B。
对union而言，要把set2所有的东西都扔到A中（缺点是也需要遍历）
初始化：
初始化时必须一次性把所有的数据样本给它，不能动态地过来（如流）
01 具体实现
代表结点代表整个集合：
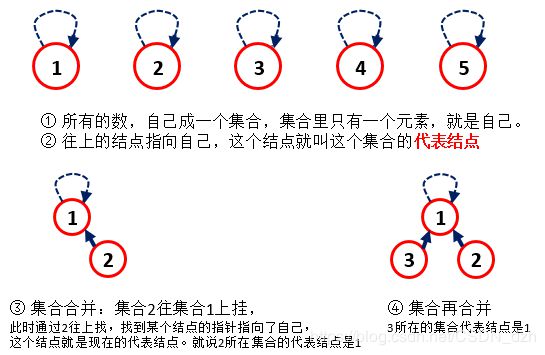
- 对于isSameSet，只需要通过元素A和元素B不断往上找直到找到各自代表结点，查它们的代表结点是否相同就可以判断它们是否在桶一个集合中。
- 对于union，首先要通过元素A和元素B不断往上找直到找到各自代表结点，让数量少的那个set挂在数量多的那个set上。合并set的代表结点是原来数量多的那个set的代表结点。
02 优化
看出每一次查询操作的时间复杂度为O(H)，H为树的高度
于是只要去查某个元素的代表结点时，都涉及下面的优化
03 代码实现
class UnionSet {
unordered_map<int, int> fatherMap; // child - father
unordered_map<int, int> sizeMap; // node - sizeOFset
public:
UnionSet(int n) {
for (int i = 1; i <= n; ++i) {
fatherMap[i] = i;
sizeMap[i] = 1;
}
}
int findRoot(int node) {
if (fatherMap[node] == node)
return node;
return findRoot(fatherMap[node]);
}
void Union(int node1, int node2) {
int root1 = findRoot(node1);
int root2 = findRoot(node2);
if (root1 == root2)
return;
if (sizeMap[root1] <= sizeMap[root2]) {
fatherMap[root1] = root2;
sizeMap[root2] += sizeMap[root1];
sizeMap.erase(root1);
} else {
fatherMap[root2] = root1;
sizeMap[root1] += sizeMap[root2];
sizeMap.erase(root2);
}
}
int getSize() {
return sizeMap.size();
}
bool isInSameSet(int node1, int node2) {
return findRoot(node1) == findRoot(node2);
}
};
刷题笔记32——STL::map实现并查集、岛问题
五、前缀树（trie树）
效率很高：
- 每个节点保存一个字符
- 根节点不保存字符
- 每个节点最多有n个子节点(n是所有可能出现字符的个数)
- 查询的复杂度为O(k)，k为查询字符串长度
功能举例：
六、B树和B+树
Ｂ树和Ｂ＋树的出现是因为一个问题——磁盘IO。所以在大量数据存储中，查询时不能一下将所有数据加载到内存中，只能逐一加载磁盘页，每个磁盘页对应树的结点。造成大量磁盘IO操作（最坏情况下为树的高度）。
- 所以，这里将树变得矮胖来减少磁盘IO的次数——采用多叉树，每个结点存储多个元素，又根据AVL得到一棵平衡多路查找树可以使得数据查找效率在O（logN）
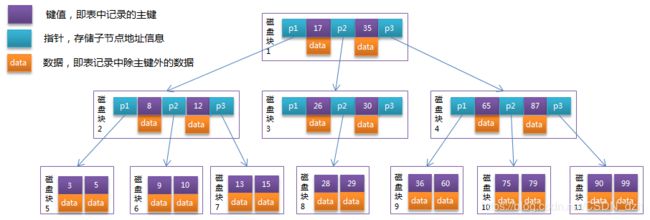
B树：
- 每个节点都存储key和value，所有的节点组成这棵树，并且叶子结点指针为null
- 一个m阶B树最多有m个孩子，若根结点不是叶子结点，则至少有 2 个孩子
- 所有叶子结点都在一层
- 先由根结点找磁盘块1，读入内存（IO第一次）；
- 比较，找指针p2；
- 根据p2指针找到磁盘块3，读入内存（IO第二次），在磁盘块3中的关键字列表中找到关键字30
综上，需2次磁盘IO操作，2次内存查找操作；由于内存在红的关键字是一个有序表结构，可以用二分法提高效率
故 3 次磁盘IO操作是影响整个B树查找效率的决定因素，它相对于AVL树缩减了结点的个数
B+树非叶子节点只存储key，只有叶子结点存储value，叶子结点包含了这棵树的所有键值，每个叶子结点有一个指向相邻叶子结点的指针，这样可以降低B树的高度
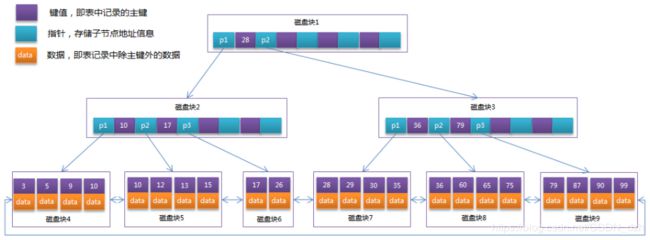
为什么B+树是数据库实现索引的首选数据结构呢？——评价一个数据结构作为索引的指标就是在查找时IO操作的次数
1、这棵树比较矮胖，树的高度越小，IO次数越少
2、一般来说，索引很大，往往以文件的形式存储在磁盘上，索引查找时产生磁盘IO消耗，相对于内存读取，IO存取的消耗比较高
聚集索引：data存数据本身，索引也是数据。数据和索引存在一个文件中。
非聚集索引：data存的是数据地址，索引是索引，数据是数据
根据B+树的结构，我们可以发现B+树相比于B树，在文件系统，数据库系统当中，更有优势，原因如下：
-
B+树单一节点存储更多的元素，使得查询的IO次数更少
B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说I/O读写次数也就降低了。 -
B+树所有查询都要查找到叶子节点，查询效率更加稳定
由于内部结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。 -
B+树所有叶子节点形成有序链表，便于范围查询，更有利于对数据库的扫描
B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题，而B+树只需要遍历叶子节点就可以解决对全部关键字信息的扫描，所以对于数据库中频繁使用的range query，B+树有着更高的性能
七、线段树
来源
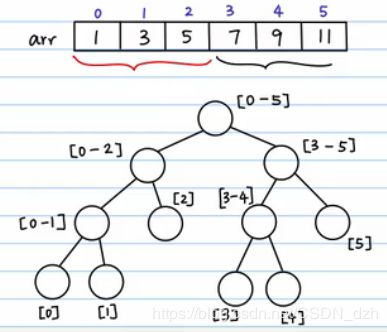
对一个很大的一维数组 arr，对里面的数字我们要反复做两个操作：
- query(arr, L, R) ：随机选一个区间 [L, R]，要把区间内的数都加起来 —— O(n)
- update(arr, i, val)：随机修改数组中的一个值 —— O(1)
那么，现在要做这两个操作，由于 query 是 O(n) 的，那么就整个过程就非常慢，有什么办法把 query 操作变成 O(1) 的吗？
- 创建一个同样大小的 sum_arr 数组，前 n 项和放到 sum_arr 对应的位置上
- 于是，sum = a - b，这样 query 的复杂度就变为 O(1)，而 update 就变成 O(n) 了
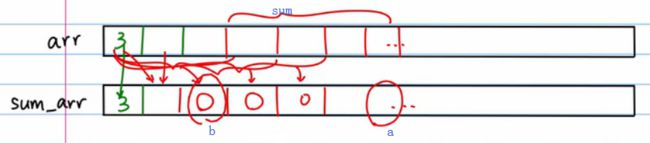
更好的办法是使用 —— 线段树，把这两个操作的复杂度都变为 O(logn)
01 线段树的优势
-
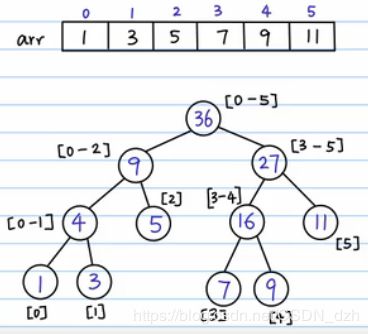
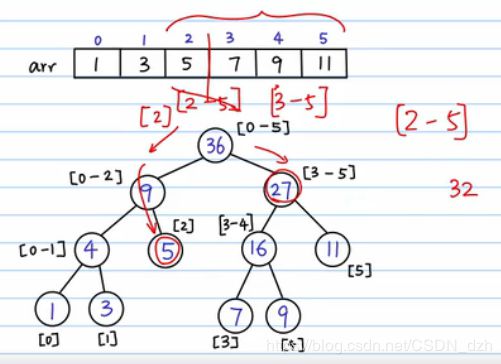
1）根结点表示数组元素的总和
-
2）分叉，把数组劈成两半。做法就是不断二分，最终所有的叶子结点就是数组中的元素
-
3）填每一个结点
-
4）有一个 query 需求，要算区间 [2, 5] 以内的和。那么我们就把这个区间分半，分成 [2] 和 [3, 5]。这样，对query，最坏情况就是把这棵树从根结点到叶子结点搜索一遍，复杂度变为了 O(logn)。
-
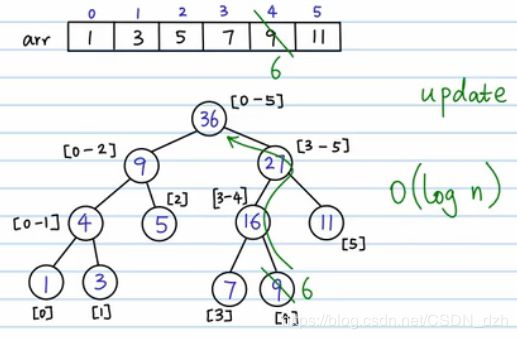
5）有另一个需求 update，要把 4 位置上的数字改为 6，那么我们就先顺着这条路找到 4 位置，然后再返回去修改这条路上的和，其他路径不会受到影响。所以总的时间复杂度也是 O(logn) 的
02 线段树实现
1）构建线段树
- 做一棵满二叉树，没有结点的地方填充虚节点。这样，根据堆结构的原理，我们能很容易求出当前结点的左右孩子。
- PS：线段树一般开 4倍arrSize 的大小
2）线段树的更新
- 从根结点开始，确定要改左分支还是右分支，找叶子结点并修改（注意 arrTmp 和 tree 数组对应的位置都要改）
- 更新之后，往上改区间和
3）线段树的查询
- 同样我们要去查询左边和右边，左边和右边的结果加起来就是我们要找的区间和
- 这个结果什么时候返回呢？换句话说，我们如何知道找到了这个结果从而结束递归呢？
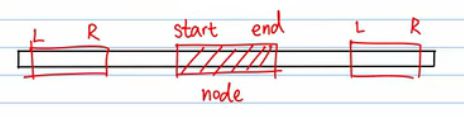
- 如果不在计算范围内，返回0。也就是说，如果我们的 [L, R] = [4, 5]，而 [start, end] = [0, 2]，就会出现在 arr 的 [0, 2] 中去找 [4, 5]，这两段区间没有重合的部分，所以直接返回 0。不在计算范围内的情况如下图所示，所以条件是
R< start || end < L
- 如果正好计算到叶节点，那么就返回叶节点上的数字。条件是
start == end，但这里的问题是，必须要递归到叶子结点，而实际上，比如我们要求 [2, 5] 区间内的和，当我们找到 [3,5] 这个区间和的时候，递归就可以结束了，不需要再往下递归到叶子结点。所以，这个条件应该改为L <= start && end <= R
class SegTree {
vector<int> tree;
vector<int> arrTmp;
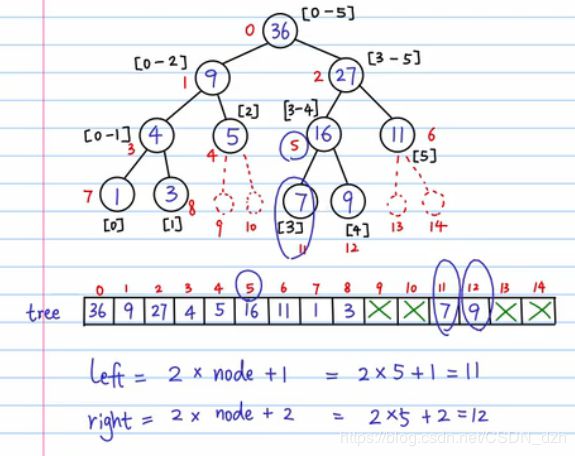
void buildTreeCore(const vector<int>& arr, int curNode, int start, int end) {
if (start == end)
tree[curNode] = arr[start];
else {
int mid = start + ((end - start) >> 1);
int leftChild = 2 * curNode + 1;
int rightChild = 2 * curNode + 2;
buildTreeCore(arr, leftChild, start, mid);
buildTreeCore(arr, rightChild, mid + 1, end);
tree[curNode] = tree[leftChild] + tree[rightChild];
}
}
void updateTreeCore(int curNode, int start, int end, int idx, int val) {
if (start == end) {
arrTmp[idx] = val;
tree[curNode] = val;
} else {
int mid = start + ((end - start) >> 1);
int leftChild = 2 * curNode + 1;
int rightChild = 2 * curNode + 2;
if (idx >= start && idx <= mid)
updateTreeCore(leftChild, start, mid, idx, val);
else
updateTreeCore(rightChild, mid + 1, end, idx, val);
tree[curNode] = tree[leftChild] + tree[rightChild];
}
}
int queryTreeCore(int curNode, int start, int end, int L, int R) {
if (R < start || end < L)
return 0;
else if (L <= start && end <= R)
return tree[curNode];
else {
int mid = start + ((end - start) >> 1);
int leftChild = 2 * curNode + 1;
int rightChild = 2 * curNode + 2;
int sumOfLeft = queryTreeCore(leftChild, start, mid, L, R);
int sumOfRight = queryTreeCore(rightChild, mid + 1, end, L, R);
return sumOfLeft + sumOfRight;
}
}
public:
void buildTree(const vector<int>& arr) {
if (arr.empty())
return;
arrTmp = arr;
int sz = arr.size();
tree = vector<int>(4 * sz, 0); // 线段树一般开4倍大小
buildTreeCore(arr, 0, 0, sz - 1);
}
void updateTree(int i, int val) {
updateTreeCore(0, 0, arrTmp.size() - 1, i, val);
}
int queryTree(int L, int R) {
return queryTreeCore(0, 0, arrTmp.size() - 1, L, R);
}
};