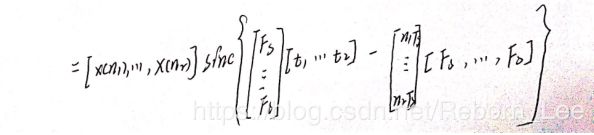【 MATLAB 】MATLAB 实现模拟信号采样后的重建（一）
为了让MATLAB数字信号处理的相关博文能够得到一个梳理，我开通了一个专栏：数字信号处理的MATLAB实现
模拟信号经过采样后得到x(n)，从x(n)中重建模拟信号
在数学上可用公式来描述：
![x_a(t)= \sum_{n = -\infty}^{\infty}x(n)sinc[F_s(t - n T_s)]](http://img.e-com-net.com/image/info8/d2244bac066646528ca7e2f5c35d9f63.gif)
式中，
是一种内插函数。
对于样本之间的内插，MATLAB提供了几种方法。产生sinc(x)函数在已知有限个样本数之下可用于实现上式，即：
如果
已知，并且如果想要在一个很细的栅格（栅格间隔
）上内插 ，那么由内插公式，可得：
这就能作为一个矩阵向量乘法运算实现，如下给出MATLAB脚本：
n = n1:n2;
t = t1:Dt:t2;
Fs = 1/Ts;
nTs = n*Ts;
xa = x * sinc( Fs*(ones(length(n),1)*t - nTs' * ones(1,length(t))));
有的人看到这里一定又懵逼了，对于这种向量化的编程不是太明白，为什么可以写成这样？这也是我关于MATLAB数字信号处理的第一篇博文所强调的：专栏，请查看第一篇博文：向量化编程实践
为了弄清楚上面的这个编程思路是如何的，向量化是如何向量化的，我给出了自己的推导，由于输入公式太过于繁琐，我也没多少时间，所以给出了手稿版本：
我不得不说，上面也提到了模拟信号的时间t用栅格间隔的表示方法是为了用MATLAB来近似画出模拟信号，我是默认你读过了我之前的博文：
【 MATLAB 】使用 MATLAB 实现模拟信号的近似及其连续傅里叶变换
这篇博文中给出了一个案例：
下面给出一个案例：
设
使用MATLAB求出并画出它的傅里叶变换。
紧接着下一篇博文，我们又同样使用了这个案例，对这个模拟信号进行了采样，使用不同的采样率采样，观察采样后的信号的DTFT：
【 MATLAB 】模拟信号采样及离散时间傅里叶变换案例分析
这篇博文，我们同样使用上面给出的案例，使用采样样本重建模拟信号，观察不同采样率下重建信号的误差。
模拟信号：
对该信号使用两种不同的采样频率采样。
a. 在 fs = 5000 对信号进行采样
b. 在 fs = 1000 对信号采样
首先讨论第一种情况：
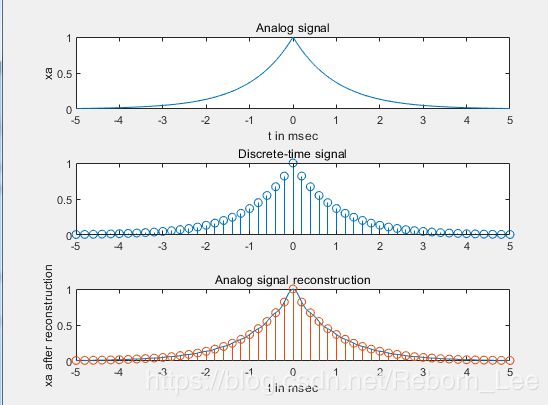
a. 在 fs = 5000 对信号进行采样
直接给出脚本：
clc
clear
close all
% Analog signal
Dt = 0.00005;
t = - 0.005:Dt:0.005;
xa = exp(-1000 * abs(t));
subplot(3,1,1);
plot(1000*t,xa);
title('Analog signal');
xlabel('t in msec');
ylabel('xa');
% Discrete-time signal
Ts = 0.0002;
Fs = 1/Ts;
n = -25:25;
nTs = n*Ts;
x = exp(-1000*abs(nTs));
subplot(3,1,2)
% plot(1000*t,xa);
% hold on
stem(n*Ts*1000,x);
title('Discrete-time signal');
% hold off
% Analog signal reconstruction
xa_r = x * sinc( Fs * ( ones(length(n),1) * t - nTs' * ones(1,length(t) ) ));
subplot(3,1,3);
plot(1000*t,xa_r);
title('Analog signal reconstruction');
xlabel('t in msec');
ylabel('xa after reconstruction');
hold on
stem(n*Ts*1000,x)
hold off
%check
error = max(abs(xa_r - xa ))
且error = 0.0363
重建的和真正的模拟信号之间的最大误差是0.0363，这是由于模拟信号xa（t）不是严格带限产生的，况且还是一个有限的样本数。重复成这个样子，已经很成功了。
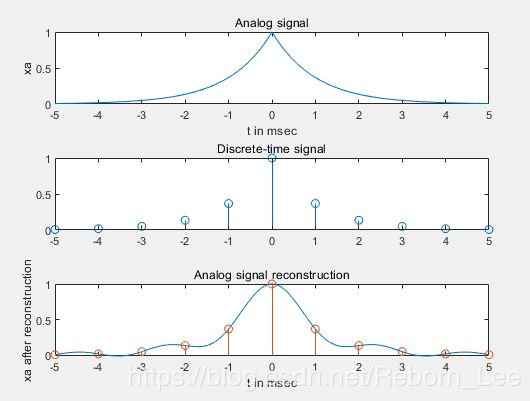
b. 在 fs = 1000 对信号采样
这时候采样间隔为1ms，模拟信号的时间范围是[-5,5]ms，也就是10ms，这时候我们可以得到11个采样间隔点，也就是得到的离散信号的范围为[-5:5]，下面直接给出MATLAB脚本：
clc
clear
close all
% Analog signal
Dt = 0.00005;
t = - 0.005:Dt:0.005;
xa = exp(-1000 * abs(t));
subplot(3,1,1);
plot(1000*t,xa);
title('Analog signal');
xlabel('t in msec');
ylabel('xa');
% Discrete-time signal
Ts = 0.001;
Fs = 1/Ts;
n = -5:5;
nTs = n*Ts;
x = exp(-1000*abs(nTs));
subplot(3,1,2)
% plot(1000*t,xa);
% hold on
stem(n*Ts*1000,x);
title('Discrete-time signal');
% hold off
% Analog signal reconstruction
xa_r = x * sinc( Fs * ( ones(length(n),1) * t - nTs' * ones(1,length(t) ) ));
subplot(3,1,3);
plot(1000*t,xa_r);
title('Analog signal reconstruction');
xlabel('t in msec');
ylabel('xa after reconstruction');
hold on
stem(n*Ts*1000,x)
hold off
%check
error = max(abs(xa_r - xa ))
只是稍微改了几个数据而已。
可见，采样率低了之后，重构的是个嘛呀！
误差：
error =
0.1852
所有的这些都是频谱混叠导致的。