算法课笔记系列（0）——Prologue and Notation

为了准备周四的期中考试，所以花时间复习前面知识的同时，也一并写一篇，就当做复习笔记了。

这一部分主要介绍了一些基本的定义和数学的证明方法。

首先，定义了集合的定义：集合是一些无序元素的集合，具有确定性、互异性和无序性。然后介绍了一部分集合的一些基本概念，如集合的基数，如|S|表示集合S的基数，即元素的个数；两个集合相等S=T是指S中每一个元素都在T中，T中的每个元素也都在S中；子集（可以包含空集）、真子集（不包含空集）、严格子集（不包含自身相等的情况），以及的集合的并、交、差、补集、笛卡尔积、幂集。

接着介绍了函数的定义，定义域Dom(f)， 值域Ran(f)，映射和操作，单射函数（一一映射），满射（Ran(f) = B）,双射（既是单射又是满射），反函数（Dom(g) = Ran(f), g(f(x)) = x）,f◦g表示domain {x| x ∈ Dom(g) ∧g(x) ∈Dom(f)},valuef (g(x)). 另外，就是注意多项式的定义，一个多项式是由变量和常数构成的有限长度的表达式，只能使用加，减，乘和非负的整数幂指数（用于判别一个表达式是否是多项式）。

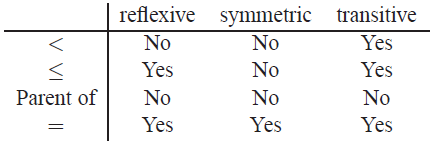
关系的定义，分为等价关系和偏序。如果A是一个集合，一个性质M(x₁,…x_n)对于Aⁿ的n行记录成立，但是不对于其余n行记录全部成立的性质称为A上的一个n元关系或者A的预测。如，性质x<y. 2 < 5,6 <4. 这里，A是整数集合。A上的一个二元关系R称为等价关系如果满足自反性、对称性和传递性；A上的一个二元关系R称为偏序如果满足反自反省和传递性。如：

         

下面是该部分的重点——证明。

1. Proof by Construction 通过构造来证明

这是最直观的一种证明方式，比如证明一个式子是奇数，就将其构造成2k+1，偶数就构造成2k，带入式子中，一步步往结论上面靠。

2. Proof by Contrapositive 通过逆否定理来证明

逆否定理可以分为通过推出矛盾和举反例。如已知p成立，要证明q成立则可以转化为￢q 而推出 ￢p。该定理的使用场景是￢q比较好列出的情况。通过推出矛盾，则是如果证明p命题为true，则转化为证明￢p是false。即假设原命题不成立，推出矛盾，则证明原假设不正确，原命题是成立的。

3. Proof by cases通过案例来证明

案例证明则是将原命题的条件分为几个子集，证明对每一个子集都成立，则推出原命题成立。

4. Proof by Mathematical Induction 通过数学归纳法来证明

数学归纳法主要是分为三个步骤(考试的时候要写清楚每一个步骤)，

Basic step：这一步主要是对前面比较小的几个数带入式子推出成立，即P(n0)成立；

Induction Hypothesis: 这一步则是假设原式对于n = k成立，即P(k)成立；

Proof of Induction Step: 这一步则是证明当n = k+1时，式子也成立。

这部分还讲了数学归纳法的两个变形，第一种是Minimal counterexample Principle, 其实就是归纳证明和Proof by contradiction的一个组合。为了证明一个命题，假设原命题是不成立的，那么至少存在一个反例。考虑到有一些规模会比较大的数，因此考虑反例的时候可以考虑存在一个反例C是最小的。然后，找出矛盾点在可以找一个比C还要小的反例使得最小假设不成立。这种方法称为无穷递减法。比如课上的例子：

           

  假设k是使得式子可以被 3整除的最小数，通过构造证明k-1也可以被3整除，小于假设k的最小性，因此推翻原假设被3整除不是对所有的n>=0成立。

  第二种变形是The strong principle of Mathematical Induction. 与传统的数学归纳法的不同点在于，第二步假设的时候，不是证明P(k)成立，而是证明对于k>=n0, 对于每一个n满足n0<=n <=k，都有P(n)成立，进而推导P(k+1)成立。

举个栗子：证明对于任意的n∈ N，n>=2, 都有质数因子。

证明：

定义P(n)为命题：n要么是质数，要么是两个或者多个质数的乘积。接下来证明对于任意的n>=2，P(n)成立。

1.     Basic step. P(2)成立，因为2是质数

2.     Induction hypothesis. 假设对于k>=2, 2 <= k <= n, P(n)都成立(Strong principle)

3.     Proof of induction step. 证明P(k+1)成立。

如果P(k+1)是质数，命题显然成立；

如果P(k+1)不是一个质数，那么根据质数的定义，k+1 = r * s, 其中r和s都是大于1小于k+1的正整数。即有 2 <=r <= k, 2 <=s <= k, 这样根据归纳假设，r和s要么是质数，要么是两个或者多个质数的乘积。那么他们的乘积k+1也就是两个或者多个质数的乘积。证得P(k+1)成立。