机器学习实战——python实现SOM神经网络聚类算法

算法基础

SOM网络结构

输入层：假设一个输入样本为X=[x1,x2,x3,…,xn]，是一个n维向量，则输入层神经元个数为n个。
输出层（竞争层）：通常输出层的神经元以矩阵方式排列在二维空间中，每个神经元都有一个权值向量。
假设输出层有m个神经元，则有m个权值向量，Wi = [wi1,wi2,....,win], 1<=i<=m。

算法流程

1. 初始化:权值使用较小的随机值进行初始化，并对输入向量和权值做归一化处理 
          X’ = X/||X|| 
          ω’i= ωi/||ωi||， 1<=i<=m 
          ||X||和||ωi||分别为输入的样本向量和权值向量的欧几里得范数。
2.将样本输入网络:样本与权值向量做点积，点积值最大的输出神经元赢得竞争，
（或者计算样本与权值向量的欧几里得距离，距离最小的神经元赢得竞争）记为获胜神经元。
3.更新权值:对获胜的神经元拓扑邻域内的神经元进行更新,并对学习后的权值重新归一化。 
        ω(t+1)= ω(t)+ η(t，n) * (x-ω(t))
        η(t，n):η为学习率是关于训练时间t和与获胜神经元的拓扑距离n的函数。
        η(t，n)=η(t)e^(-n)
        η(t)一般取迭代次数的倒数

4.更新学习速率η及拓扑邻域N,N随时间增大距离变小。
5.判断是否收敛。如果学习率η<=ηmin或达到预设的迭代次数，结束算法。

算法实现

#初始化输入层与竞争层神经元的连接权值矩阵
def initCompetition(n , m , d):
    #随机产生0-1之间的数作为权值
    array = random.random(size=n * m *d)
    com_weight = array.reshape(n,m,d)
    return com_weight

#计算向量的二范数
def cal2NF(X):
    res = 0
    for x in X:
        res += x*x
    return res ** 0.5

#对数据集进行归一化处理
def normalize(dataSet):
    old_dataSet = copy(dataSet)
    for data in dataSet:
        two_NF = cal2NF(data)
        for i in range(len(data)):
            data[i] = data[i] / two_NF
    return dataSet , old_dataSet
#对权值矩阵进行归一化处理
def normalize_weight(com_weight):
    for x in com_weight:
        for data in x:
            two_NF = cal2NF(data)
            for i in range(len(data)):
                data[i] = data[i] / two_NF
    return com_weight

#得到获胜神经元的索引值
def getWinner(data , com_weight):
    max_sim = 0
    n,m,d = shape(com_weight)
    mark_n = 0
    mark_m = 0
    for i in range(n):
        for j in range(m):
            if sum(data * com_weight[i,j]) > max_sim:
                max_sim = sum(data * com_weight[i,j])
                mark_n = i
                mark_m = j
    return mark_n , mark_m

#得到神经元的N邻域
def getNeibor(n , m , N_neibor , com_weight):
    res = []
    nn,mm , _ = shape(com_weight)
    for i in range(nn):
        for j in range(mm):
            N = int(((i-n)**2+(j-m)**2)**0.5)
            if N<=N_neibor:
                res.append((i,j,N))
    return res

#学习率函数
def eta(t,N):
    return (0.3/(t+1))* (math.e ** -N)

#SOM算法的实现
def do_som(dataSet , com_weight, T , N_neibor):
''' T:最大迭代次数 N_neibor:初始近邻数 '''
    for t in range(T-1):
        com_weight = normalize_weight(com_weight)
        for data in dataSet:
            n , m = getWinner(data , com_weight)
            neibor = getNeibor(n , m , N_neibor , com_weight)
            for x in neibor:
                j_n=x[0];j_m=x[1];N=x[2]
                #权值调整
                com_weight[j_n][j_m] = com_weight[j_n][j_m] + eta(t,N)*(data - com_weight[j_n][j_m])
            N_neibor = N_neibor+1-(t+1)/200
    res = {}
    N , M , _ =shape(com_weight)
    for i in range(len(dataSet)):
        n, m = getWinner(dataSet[i], com_weight)
        key = n*M + m
        if res.has_key(key):
            res[key].append(i)
        else:
            res[key] = []
            res[key].append(i)
    return res

#SOM算法主方法
def SOM(dataSet,com_n,com_m,T,N_neibor):
    dataSet, old_dataSet = normalize(dataSet)
    com_weight = initCompetition(com_n,com_m,shape(dataSet)[1])
    C_res = do_som(dataSet, com_weight, T, N_neibor)
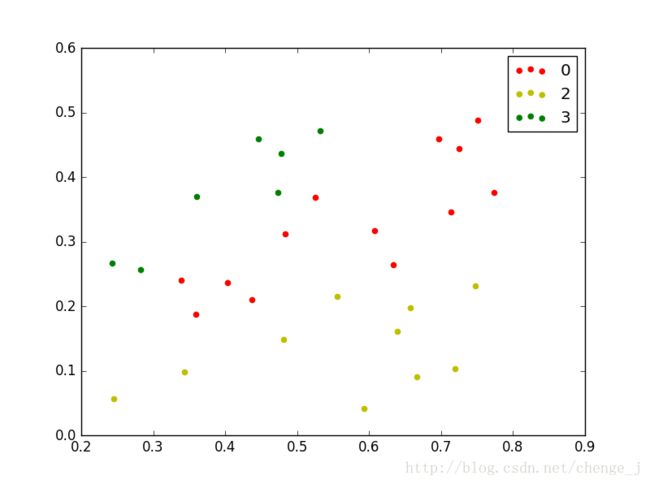
    draw(C_res, dataSet)
    draw(C_res, old_dataSet)

结果测试

测试数据（来源于西瓜书）

0.697,0.46
0.774,0.376
0.634,0.264
0.608,0.318
0.556,0.215
0.403,0.237
0.481,0.149
0.437,0.211
0.666,0.091
0.243,0.267
0.245,0.057
0.343,0.099
0.639,0.161
0.657,0.198
0.36,0.37
0.593,0.042
0.719,0.103
0.359,0.188
0.339,0.241
0.282,0.257
0.748,0.232
0.714,0.346
0.483,0.312
0.478,0.437
0.525,0.369
0.751,0.489
0.532,0.472
0.473,0.376
0.725,0.445
0.446,0.459

画图方法

def draw(C , dataSet):
    color = ['r', 'y', 'g', 'b', 'c', 'k', 'm' , 'd']
    count = 0
    for i in C.keys():
        X = []
        Y = []
        datas = C[i]
        for j in range(len(datas)):
            X.append(dataSet[datas[j]][0])
            Y.append(dataSet[datas[j]][1])
        plt.scatter(X, Y, marker='o', color=color[count % len(color)], label=i)
        count += 1
    plt.legend(loc='upper right')
    plt.show()

测试代码及方法参数

#数据处理的方法可以参见上一篇博客——DBSCAN算法
dataSet = loadDataSet("dataSet.txt")
SOM(dataSet,2,2,4,2)

聚类结果

按照归一化的数据绘制的聚类结果

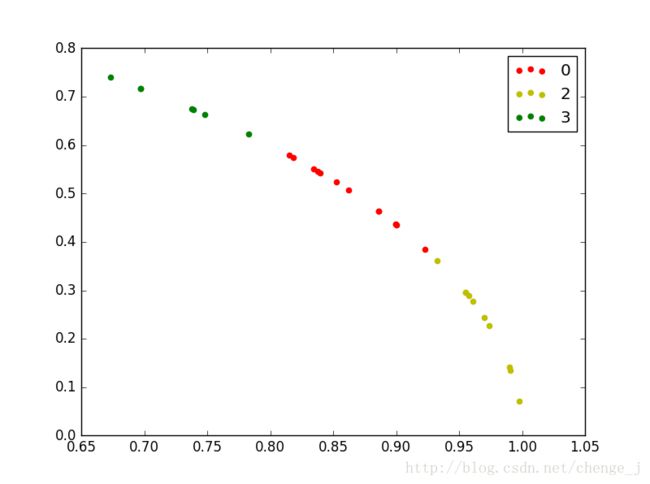
按照原数据绘制的聚类结果