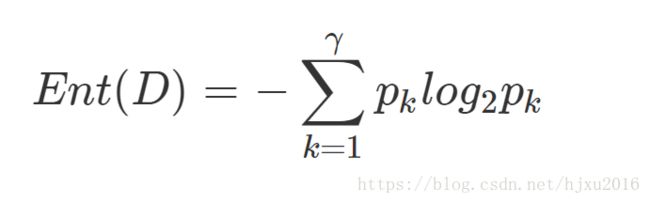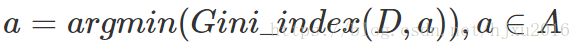机器学习实战笔记(二)决策树
之前介绍的K-近邻算法可以完成很多分类任务,但是最大的缺点是无法给出数据的内在含义,而决策树很好的解决了这个问题.
决策树的优点:计算不复杂,输出易于理解,但缺点也很明显,可能会过拟合.
先简单提几个西瓜书中的概念,这里转自https://blog.csdn.net/volvet/article/details/55223569
信息增益
信息熵可以用来衡量样本集合纯度. 假定 样本集合D
, 其中第k类样本所占比例为pk(k=1,2,...,γ)
, 则D的熵为
熵越小, 则样本集合纯度越高, 以信息论的角度看, 也就是信息量越小.
假定离散属性a
有V个可能的取值 {a1,a2,...,av}, 使用a来对样本集合D进行划分, 产生V个分支节点. 其中第v个分支节点包含D中所有取值为av的样本, 记为Dv. 我们可以根据上面的公式计算Dv的信息熵, 于是可以计算用属性a
划分的信息增益, 计算方法为:
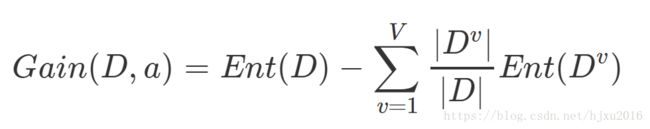
信息增益越大, 也就是使用属性 a划分所获得纯度提升越大, 因此我们可以用信息增益来决定决策树的划分属性. 这就是著名的ID3决策树学习算法(Iterative Dichotomiser 3).
增益率
使用信息增益进行决策树划分, 会偏好可取值数目多的属性, 可能导致决策树泛化能力弱, 为了解决这个问题, 引入了增益率, 其定义如下:
这就是C4.5决策树学习算法.
基尼指数
数据集的纯度也可以用基尼指数来度量:
则属性a划分后的基尼指数为
按照机器学习实战这本书的进度,暂时按照ID3来够着决策树
决策树的创建是一个递归的过程,可以这样理解
寻找划分数据集最好的特征,划分数据集,创建分支节点,
再对每个划分的数据集,调用递归函数,增加返回结果到分支节点中,具体在代码注释中详细解释
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon Jul 12 07:12:59 2018
@author: hjxu
"""
import math
import operator
def calcDEnt(dataSet):
'''
:param dataSet: 数据集
:return: 熵
'''
numEntries = len(dataSet) #得到数据的个数
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
returnEnt = 0.0
for key in labelCounts:
prob = float(1.0 * labelCounts[key]/numEntries)
returnEnt -= prob * math.log(prob, 2)
return returnEnt
def createDataSet(): # labels代表的是特征的名字
'''
:return: 数据特征集 和每一个特征对应的名字
'''
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels
def splitDataSet(dataSet, axis, value):
'''
:param dataSet: 待划分的数据集
:param axis: 划分数据的特征
:param value: 需要返回的特征值
:return: 将符合的元素抽取出来
'''
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedVec = featVec[:axis]
reducedVec.extend(featVec[axis+1:])
retDataSet.append(reducedVec)
return retDataSet
def chooseBestFeatureSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
baseEnt = calcDEnt(dataSet) # 计算一个基础的熵,这个熵为全局熵
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueFeat = set(featList)
newEnt = 0.0
for val in uniqueFeat:
subData = splitDataSet(dataSet, i, val)
prob = len(subData)/float(len(dataSet))
newEnt += prob * calcDEnt(subData)
InfoGain = baseEnt - newEnt # 求信息增益
if(InfoGain > bestInfoGain):
bestInfoGain = InfoGain
bestFeature = i
return bestFeature
def majorityCnt(classList):
classCount = {}
for classVal in classList:
if(classVal not in classCount.keys()):
classCount[classVal] = 0
classCount += 1
sortedCount = sorted(classCount.iteritems(), key=operator.itemgetter, reverse=True)
return sortedCount[0][0]
def createTree(dataSet, labels):
'''
生成树,调用递归,返回的条件有两个,样本都属于同一类别,则返回这个类别
如果特征都用光了,则返回数量最多的
'''
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(dataSet):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
subLabels = labels[:]
del(subLabels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for val in uniqueVals:
subLabels = subLabels[:]
myTree[bestFeatLabel][val] = createTree(splitDataSet(dataSet, bestFeat, val), subLabels)
return myTree
def classify(inputTree, featLabels, testVec):
'''
:param inputTree:生成的树
:param featLabels: 特征向量每一列对应的标签,也可以成每一列是什么特征
:param testVec: 特征向量
:return:
'''
# firstStr = inputTree.keys()[0]
firstSides = list(inputTree.keys())
firstStr = firstSides[0]
secondDic = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
for key in secondDic.keys():
if testVec[featIndex] == key:
if type(secondDic[key]).__name__ == 'dict':
classLabel = classify(secondDic[key], featLabels, testVec)
else:
classLabel = secondDic[key]
return classLabel
def getNumberLeafs(myTree):#获取叶子的数量
numLeaf = 0
firstSides = list(myTree.keys())
firstStr = firstSides[0]
sedcondDic = myTree[firstStr]
for key in sedcondDic.keys():
if type(sedcondDic[key]).__name__ == 'dict':
numLeaf += getNumberLeafs(sedcondDic)
else:
numLeaf += 1
return numLeaf
def getTreeDepth(myTree):#得到树的高度
maxDepth = 0
firstSides = list(myTree.keys())
firstStr = firstSides[0]
sedcondDic = myTree[firstStr]
for key in sedcondDic.keys():
if type(sedcondDic[key]).__name__ == 'dict':
thisDepth = 1 + getNumberLeafs(sedcondDic)
else:
thisDepth = 1
if thisDepth > maxDepth:
maxDepth = thisDepth
return maxDepth
def storeTree(inputTree, saveName):#保存树
import pickle
fw = open(saveName)
pickle.dump(inputTree, 'w')
fw.close()
def loadTree(filename):#加载树
import pickle
fr = open(filename)
return pickle.load(fr)
def test1(): # 查看 计算的熵的值
myData, labels = createDataSet()
print (myData)
Ent = calcDEnt(myData)
print(Ent)
myData[0][-1] = 'maybe'
Ent = calcDEnt(myData)
print(Ent)
def test2(): #预测以及查看树
myDat, labels = createDataSet()
myTree = createTree(myDat, labels)
print(myTree)
predict = classify(myTree, labels, [1, 1])
print(predict)
def test3():#从文本中导入数据
fr = open('./lenses.txt')
lenses = [inst.strip().split('\t') for inst in fr]
lensesLabel = ['age', 'prescript', 'astigmatic', 'tearRate']
lensesTree = createTree(lenses, lensesLabel)
print (lensesTree)
import treePlotter as tp
tp.createPlot(lensesTree)
if __name__ == '__main__':
# test1()
# test2()
test3()