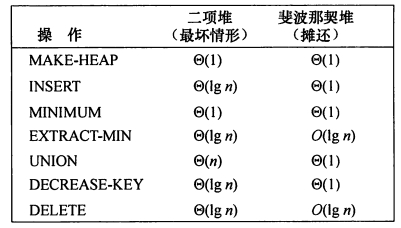
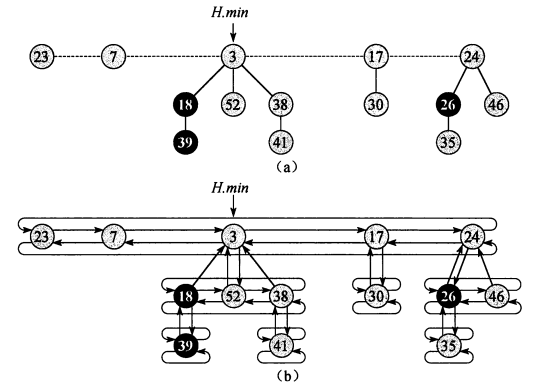
斐波那契堆
1. 结构
斐波那契堆是一系列具有最小堆序的有根树的集合, 同一代 (层) 结点由双向循环链表链接, 为了便于删除最小结点, 还需要维持链表为升序, 即 nd<=nd.right(nd==nd.right 时只有一个结点或为 None), 父子之间都有指向对方的指针.
结点有 degree 属性, 记录孩子的个数, mark 属性用来标记 (为了满足势函数, 达到摊还需求的)
2. 势函数
Φ(H)=t(H)+2m(h) Φ ( H ) = t ( H ) + 2 m ( h )
t 是根链表中树的数目, m(H) 表示被标记的结点数
最初没有结点
3. 最大度数
D(n)⩽⌊lgn⌋ D ( n ) ⩽ ⌊ l g n ⌋

4. 操作
4.1. 创建一个斐波那契堆
O(1) O ( 1 )
4.2. 插入一个结点
nd = new node
nd.prt = nd.chd = None
if H.min is None:
creat H with nd
H.min = nd
else:
insert nd into H's root list if H.min
ΔΦ=Δt(H)+2Δm(H)=1+0=1 Δ Φ = Δ t ( H ) + 2 Δ m ( H ) = 1 + 0 = 1
摊还代价为 O(1) O ( 1 )
4.3. 寻找最小结点
直接用 H.min, O(1) O ( 1 )
4.4. 合并两个斐波那契堆
def union(H1,H2):
if H1.min ==None or (H1.min and H2.min and H1.min>H2.min):
H1.min = H2.min
link H2.rootList to H1.rootList
return H1易知 ΔΦ=0 Δ Φ = 0
4.5. 抽取最小值
抽取最小值, 一定是在根结点, 然后将此根结点的所有子树的根放在 根结点双向循环链表中, 之后还要进行树的合并. 以使每个根结点的度不同,
def extract-min(H):
z = H.min
if z!=None:
for chd of z:
link chd to H.rootList
chd.prt = None
remove z from the rootList of H
if z==z.right:
H.min = None
else:
H.min = z.right
consolidate(H)
H.n -=1
return zconsolidate 函数使用一个 辅助数组 degree 来记录所有根结点 (不超过 lgn) 对应的度数, degree[i] = nd 表示. 有且只有一个结点 nd 的度数为 i.
def consolidate(H):
initialize degree with None
for nd in H.rootList:
d = nd.degree
while degree[d] !=None:
nd2 = degree[d]
if nd2.degree < nd.degree:
nd2,nd = nd,nd2
make nd2 child of nd
nd.degree = d+1
nd.mark = False # to balace the potential
remove nd2 from H.rootList
degree[d] = None
d+=1
else: degree[d] = nd
for i in degree:
if i!=None:
link i to H.rootList
if H.min ==None: H.min = i
else if H.min>i: H.min = i时间复杂度为 O(lgn) O ( l g n ) 即数组移动的长度, 而最多有 lgn 个元素
4.6. 关键字减值
def decrease-key(H,x,k):
if k>x.key: error
x.key = k
y=x.p
if y!=None and x.key < y.key:
cut(H,x,y)
cascading-cut(H,y)
if x.key < H.min.key:
H.min = x
def cut(H,x,y):
remove x from the child list of y, decrementing y.degree
add x to H.rootList
x.prt = None
x.mark = False
def cascading-cut(H,y):
z- y,prt
if z !=None:
if y.mark ==False:y.mark = True
else:
cut(H,y,z)
cascading-cut(H,z)4.7. 删除结点
decrease(H,nd, MIN)
extract-min(H)