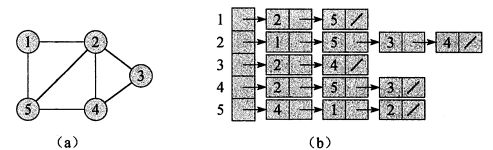
图算法

1. 图

1.1. 概念

• 顶
• 顶点的度 d
• 边
• 相邻
• 重边
• 环
• 完全图: 所有顶都相邻
• 二分图: V(G)=X∪Y,X∩Y=∅ V ( G ) = X ∪ Y , X ∩ Y = ∅ , X 中, Y 中任两顶不相邻
• 轨道
• 圈

1.1.1. 性质

• ∑v∈Vd(v)=2|E| ∑ v ∈ V d ( v ) = 2 | E |
• G 是二分图 ⇔ ⇔ G 无奇圈
• 树是无圈连通图
• 树中, |E|=|V|−1 | E | = | V | − 1

1.2. 图的表示

• 邻接矩阵
• 邻接链表
  

1.3. 树

无圈连通图, E=V−1 E = V − 1 , 详细见树,

2. 搜索–求图的生成树 1

2.1. BFS

for v in V:
    v.d = MAX
    v.pre = None
    v.isFind = False
root. isFind = True
root.d = 0
que = [root]
while que !=[]:
    nd = que.pop(0)
    for v in Adj(nd):
        if not v.isFind :
            v.d = nd.d+1
            v.pre = nd
            v.isFind = True
            que.append(v)

时间复杂度 O(V+E) O ( V + E )

2.2. DFS

Θ(V+E) Θ ( V + E )

def dfs(G):
    time = 0
    for v in V:
        v.pre = None
        v.isFind = False
    for v in V : # note this, 
        if not v.isFind:
            dfsVisit(v)
    def dfsVisit(G,u):
        time =time+1
        u.begin = time
        u.isFind = True
        for v in Adj(u):
            if not v.isFind:
                v.pre = u
                dfsVisit(G,v)
        time +=1
        u.end = time  

begin, end 分别是结点的发现时间与完成时间

2.2.1. DFS 的性质

• 其生成的前驱子图 Gpre G p r e 形成一个由多棵树构成的森林, 这是因为其与 dfsVisit 的递归调用树相对应
• 括号化结构
  
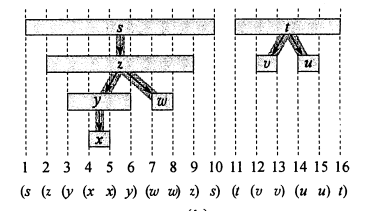
• 括号化定理:
  考察两个结点的发现时间与结束时间的区间 [u,begin,u.end] 与 [v.begin,v.end]
  
  • 如果两者没有交集, 则两个结点在两个不同的子树上 (递归树)
  • 如果 u 的区间包含在 v 的区间, 则 u 是 v 的后代

2.3. 拓扑排序

利用 DFS, 结点的完成时间的逆序就是拓扑排序

同一个图可能有不同的拓扑排序

2.4. 强连通分量

在有向图中, 强连通分量中的结点互达
定义 Grev G r e v 为 G G 中所有边反向后的图

将图分解成强连通分量的算法
在 Grev 上根据 G 中结点的拓扑排序来 dfsVisit, 即

compute Grev
initalization
for v in topo-sort(G.V):
    if not v.isFind: dfsVisit(Grev,v)

然后得到的 DFS 森林 (也是递归树森林) 中每个树就是一个强连通分量

3. 最小生成树

利用了贪心算法,

3.1. Kruskal 算法

总体上, 从最开始 每个结点就是一颗树的森林中 (不相交集合, 并查集), 逐渐添加不形成圈的 (两个元素不再同一个集合), 最小边权的边.

edges=[]
for  edge as u,v in sorted(G.E):
    if find-set(u) != find-set(v):
        edges.append(edge)
        union(u,v)
return edges

如果并查集的实现采用了 按秩合并与路径压缩技巧, 则 find 与 union 的时间接近常数
所以时间复杂度在于排序边, 即 O(ElgE) O ( E l g E ) , 而 E<V2 E < V 2 , 所以 lgE=O(lgV) l g E = O ( l g V ) , 时间复杂度为 O(ElgV) O ( E l g V )

3.2. Prim 算法

用了 BFS, 类似 Dijkstra 算法
从根结点开始 BFS, 一直保持成一颗树

for v in V: 
    v.minAdjEdge = MAX
    v.pre = None
root.minAdjEdge = 0
que = priority-queue (G.V)  # sort by minAdjEdge
while not que.isempty():
    u = que.extractMin()
    for v in Adj(u):
        if v in que and v.minAdjEdge>w(u,v):
            v.pre = u
            v.minAdjEdge = w(u,v)

• 建堆 O(V) O ( V ) //note it's v, not vlgv
• 主循环中
  
  • extractMin: O(VlgV) O ( V l g V )
  • in 操作 可以另设标志位, 在常数时间完成, 总共 O(E) O ( E )
  • 设置结点的 minAdjEdge, 需要 O(lgv) O ( l g v ) , 循环 E 次, 则 总共 O(ElgV) O ( E l g V )

综上, 时间复杂度为 O(ElgV) O ( E l g V )
如果使用的是 斐波那契堆, 则可改进到 O(E+VlgV) O ( E + V l g V )

4. 单源最短路

求一个结点到其他结点的最短路径, 可以用 Bellman-ford 算法, 或者 Dijkstra 算法.
定义两个结点 u,v 间的最短路

δ(u,v)={min(w(path)),u−→−pathvMAX,u↛v δ ( u , v ) = { m i n ( w ( p a t h ) ) , u → p a t h v M A X , u ↛ v

问题的变体
* 单目的地最短路问题: 可以将所有边反向转换成求单源最短路问题
* 单结点对的最短路径
* 所有结点对最短路路径

4.1. 负权重的边

Dijkstra 算法不能处理, 只能用 Bellman-Ford 算法,
而且如果有负值圈, 则没有最短路, bellman-ford 算法也可以检测出来

4.2. 初始化

def initialaize(G,s):
    for v in G.V:
        v.pre = None
        v.distance = MAX
    s.distance = 0

4.3. 松弛操作

def relax(u,v,w):
    if v.distance > u.distance + w:
        v.distance = u.distance + w:
         v.pre = u

性质
* 三角不等式: δ(s,v)⩽δ(s,u)+w(u,v) δ ( s , v ) ⩽ δ ( s , u ) + w ( u , v )
* 上界: v.distance⩾δ(s,v) v . d i s t a n c e ⩾ δ ( s , v )
* 收敛: 对于某些结点 u,v 如果 s->…->u->v 是图 G 中的一条最短路径，并且在对边，进行松弛前任意时间有 u.distance=δ(s,u) u . d i s t a n c e = δ ( s , u ) 则在之后的所有时间有 v.distance=δ(s,v) v . d i s t a n c e = δ ( s , v )
* 路径松弛性质: 如果 p=v0v1…vk p = v 0 v 1 … v k 是从源结点下 v0 到结点 vk 的一条最短路径，并且对 p 中的边所进行松弛的次序为 (v0,v1),(v1,v2),…,(vk−1,vk) ( v 0 , v 1 ) , ( v 1 , v 2 ) , … , ( v k − 1 , v k ) , 则 vk.distance=δ(s,vk) v k . d i s t a n c e = δ ( s , v k )
该性质的成立与任何其他的松弛操作无关，即使这些松弛操作是与对 p 上的边所进行的松弛操作穿插进行的。

证明

4.4. 有向无环图的单源最短路问题

def dag-shortest-path(G,s):
    initialize(G,s)
    for u in topo-sort(G.V):
        for v in Adj(v):
            relax(u,v,w(u,v))

4.5. Bellman-Ford 算法

def bellman-ford(G,s):
    initialize(G,s)
    for ct in range(|V|-1): # v-1times
        for u,v as edge in E:
            relax(u,v,w(u,v))
    for u,v as edge in E:
        if v.distance > u.distance + w(u,v):
            return False
    return True

第一个 for 循环就是进行松弛操作, 最后结果已经存储在 结点的 distance 和 pre 属性中了, 第二个 for 循环利用三角不等式检查有不有负值圈.

下面是证明该算法的正确性

4.6. Dijkstra 算法

def dijkstra(G,s):
    initialize(G,s)
    paths=[]
    q = priority-queue(G.V) # sort by distance
    while not q.empty():
        u = q.extract-min()
        paths.append(u)
        for v in Adj(u):
            relax(u,v,w(u,v))

5. 所有结点对的最短路问题

5.1. 矩阵乘法

使用动态规划算法, 可以得到最短路径的结构
设 l(m)ij l i j ( m ) 为从结点 i 到结点 j 的至多包含 m 条边的任意路径的最小权重, 当 m = 0, 此时 i=j, 则 为 0,
可以得到递归定义

l(m)ij=min(l(m−1)ij,min1⩽k⩽n(l(m−1)ik+wkj))=min1⩽k⩽n(l(m−1)ik+wkj)) l i j ( m ) = min ( l i j ( m − 1 ) , min 1 ⩽ k ⩽ n ( l i k ( m − 1 ) + w k j ) ) = min 1 ⩽ k ⩽ n ( l i k ( m − 1 ) + w k j ) )

由于是简单路径, 则包含的边最多为 |V|-1 条, 所以

δ(i,j)=l(|V|−1)ij=l(|V|)ij=l(|V|+1)ij=... δ ( i , j ) = l i j ( | V | − 1 ) = l i j ( | V | ) = l i j ( | V | + 1 ) = . . .

所以客户处自底向上计算, 如下
输入权值矩阵 W(wij)),L(m−1) W ( w i j ) ) , L ( m − 1 ) , 输出 L(m) L ( m ) , 其中 L(1)=W L ( 1 ) = W ,

n = L.rows
L' = new matrix(nxn) for i in range(n): for j in range(n): l'[i][j] = MAX
        for k in range(n):
            l'[i][j] = min(l'[i][j], l[i][k]+w[k][j])
return L'

可以看出该算法与矩阵乘法的关系
L(m)=Wm L ( m ) = W m ,
所以可以直接计算乘法, 每次计算一个乘积是 O(V3) O ( V 3 ) , 计算 V 次, 所以总体 O(V4) O ( V 4 ) , 使用矩阵快速幂可以将时间复杂度降低为 O(V3lgV) O ( V 3 l g V )

def f(W):
    L = W
    i = 1
    while i2
    return L

5.2. Floyd-Warshall 算法

同样要求可以存在负权边, 但不能有负值圈. 用动态规划算法:
设 d(k)ij d i j ( k ) 为 从 i 到 j 所有中间结点来自集合 {1,2,…,k} { 1 , 2 , … , k } 的一条最短路径的权重. 则有

d(k)ij={wij,k=0min(d(k−1)ij,d(k−1)ik+d(k−1)kj),k⩾1 d i j ( k ) = { w i j , k = 0 m i n ( d i j ( k − 1 ) , d i k ( k − 1 ) + d k j ( k − 1 ) ) , k ⩾ 1

而且为了找出路径, 需要记录前驱结点, 定义如下前驱矩阵 Π Π , 设 π(k)ij π i j ( k ) 为 从 i 到 j 所有中间结点来自集合 {1,2,…,k} { 1 , 2 , … , k } 的最短路径上 j 的前驱结点
则

π(0)ij={nil,i=j or wij=MAXi,i≠jand wij<MAX π i j ( 0 ) = { n i l , i = j   o r   w i j = M A X i , i ≠ j a n d   w i j < M A X

对 k⩾1 k ⩾ 1

π(k)ij={π(k−1)ij,d(k−1)ij⩽d(k−1)ik+d(k−1)kjπ(k−1)kj,otherwise π i j ( k ) = { π i j ( k − 1 ) , d i j ( k − 1 ) ⩽ d i k ( k − 1 ) + d k j ( k − 1 ) π k j ( k − 1 ) , o t h e r w i s e

由此得出此算法

def floyd-warshall(w):
    n = len(w)
    d= w
    initial pre # 0
    for k in range(n):
        d2 = d.copy()
        pre2 = pre.copy()
        for j in range(n):
            for i in range(v)
                if d[i][j] > d[i][k]+d[k][j]:
                    d2[i][j] = min(d[i][j], d[i][k]+d[k][j])
                    pre2[i][j] = pre[k][j]
        pre = pre2
        d = d2
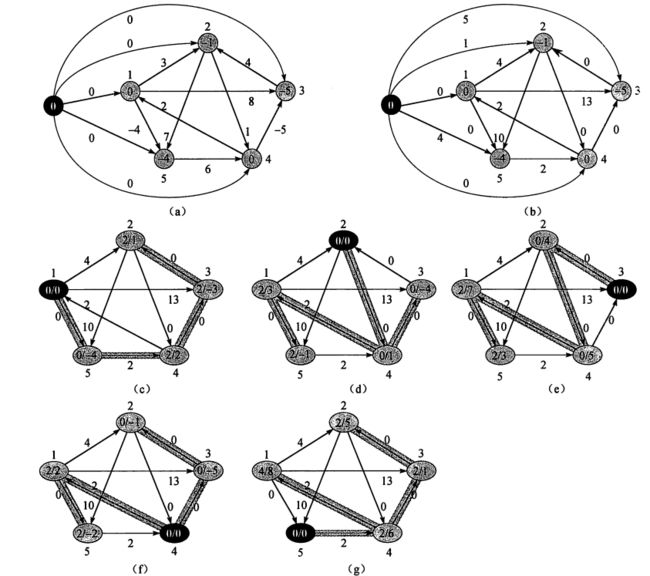
return d,pre

5.3. Johnson 算法

思路是通过重新赋予权重, 将图中负权边转换为正权, 然后就可以用 dijkstra 算法 (要求是正值边) 来计算一个结点到其他所有结点的, 然后对所有结点用 dijkstra

1. 首先构造一个新图 G’
   先将 G 拷贝到 G’, 再添加一个新结点 s, 添加 G.V 条边, s 到 G 中顶点的, 权赋值为 0
2. 用 Bellman-Ford 算法检查是否有负值圈, 如果没有, 同时求出 δ(s,v)记为h(v) δ ( s , v ) 记 为 h ( v )
3. 求新的非负值权, w’(u,v) = w(u,v)+h(u)-h(v)
4. 对所有结点在 新的权矩阵 w’上 用 Dijkstra 算法
   

JOHNSON (G, u) 

s = newNode
G' = G.copy() G'.addNode(s)
for v in G.V: G'.addArc(s,v,w=0) if BELLMAN-FORD(G' , w, s) ==FALSE 
    error "the input graph contains a negative-weight cycle" 

for v in G'.V: # computed by the bellman-ford algorithm, delta(s,v) is the shortest distance from s to v h(v) = delta(s,v) for edge(u,v) in G'.E:
    w' = w(u,v)+h(u)-h(v) d = matrix(n,n) for u in G: dijkstra(G,w',u) # compute delta' for all v in G.V
    for v in G.V:
        d[u][v] = delta'(u,v) + h(v)-h(u) return d

6. 最大流

G 是弱连通严格有向加权图, s 为源, t 为汇, 每条边 e 容量 c(e), 由此定义了网络 N(G,s,t,c(e)),
* 流函数 f(e):E→R f ( e ) : E → R

(1)(2)0⩽f(e)⩽c(e),e∈E∑e∈α(v)f(e)=∑e∈β(v)f(e),v∈V−{s,t} ( 1 ) 0 ⩽ f ( e ) ⩽ c ( e ) , e ∈ E ( 2 ) ∑ e ∈ α ( v ) f ( e ) = ∑ e ∈ β ( v ) f ( e ) , v ∈ V − { s , t }

其中 α(v) α ( v ) 是以 v 为头的边集, β(v) β ( v ) 是以 v 为尾的边集
* 流量: F=∑e∈α(t)f(e)−∑e∈−β(t)f(e), F = ∑ e ∈ α ( t ) f ( e ) − ∑ e ∈ − β ( t ) f ( e ) ,
* 截 (S,S¯¯¯) ( S , S ¯ ) : S⊂V,s∈S,t∈S¯¯¯=V−S S ⊂ V , s ∈ S , t ∈ S ¯ = V − S
* 截量 C(S)=∑e∈(S,S¯¯¯¯)c(e) C ( S ) = ∑ e ∈ ( S , S ¯ ) c ( e )

6.1. 定理 [^2]

• 对于任一截 (S,S¯¯¯) ( S , S ¯ ) , 有 F=∑e∈(S,S¯¯¯¯)f(e)−∑e∈(S¯¯¯¯,S)f(e), F = ∑ e ∈ ( S , S ¯ ) f ( e ) − ∑ e ∈ ( S ¯ , S ) f ( e ) ,
  
• F⩽C(S) F ⩽ C ( S )
  证明: 由上面定理
  
  F=∑e∈(S,S¯¯¯¯)f(e)−∑e∈(S¯¯¯¯,S)f(e), F = ∑ e ∈ ( S , S ¯ ) f ( e ) − ∑ e ∈ ( S ¯ , S ) f ( e ) ,
  
  而 0⩽f(e)⩽c(e) 0 ⩽ f ( e ) ⩽ c ( e ) , 则
  
  F⩽∑e∈(S,S¯¯¯¯)f(e)⩽∑e∈(S,S¯¯¯¯)c(e)=C(S) F ⩽ ∑ e ∈ ( S , S ¯ ) f ( e ) ⩽ ∑ e ∈ ( S , S ¯ ) c ( e ) = C ( S )
• 最大流, 最小截: 若 F=C(S) F = C ( S ) , 则 F’是最大流量, C(S) 是最小截量

6.2. 多个源, 汇

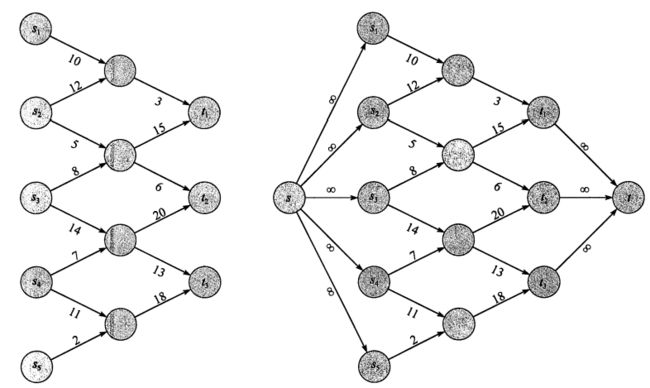
可以新增一个总的源, 一个总的汇,

6.3. Ford-Fulkerson 方法

由于其实现可以有不同的运行时间, 所以称其为方法, 而不是算法.
思路是 循环增加流的值, 在一个关联的” 残存网络” 中寻找一条” 增广路径”, 然后对这些边进行修改流量. 重复直至残存网络上不再存在增高路径为止.

def ford-fulkerson(G,s,t):
    initialize flow f to 0
    while exists an augmenting path p in residual network Gf:
        augment flow f along p
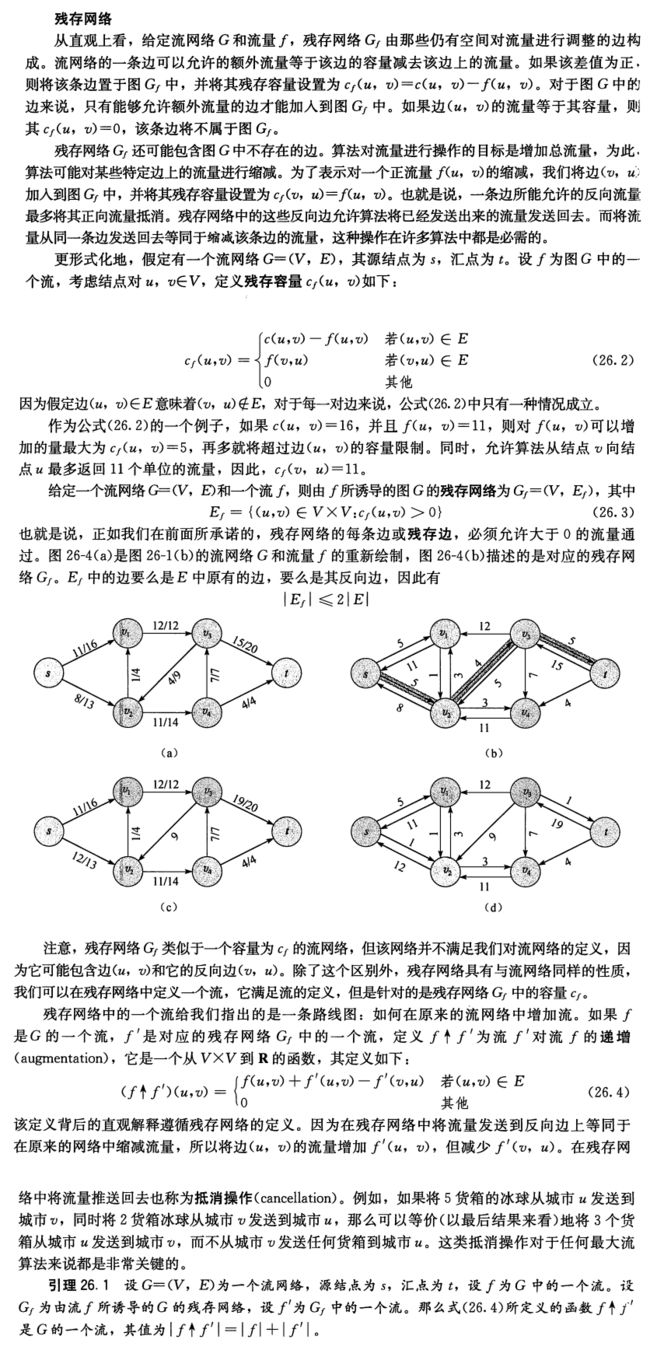
    return f

6.3.1. 残存网络

6.3.2. 增广路径

6.3.3. 割

6.4. 基本的 Ford-Fulkerson 算法

def ford-fulkerson(G,s,t):
    for edge in G.E: edge.f = 0
    while exists path p:s->t  in Gf:
        cf(p) = min{cf(u,v):(u,v) is in p}
        for edge in p:
            if edge  in E:
                edge.f +=cf(p)
            else: reverse_edge.f -=cf(p)

6.5. TBD

7. 参考资料

1. 算法导论
   [^2]: 图论, 王树禾 ↩