算法学习笔记(4)-快速排序

一、什么是快排

快速排序是图灵奖得主 C. R. A. Hoare 于 1960 年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。分治法的基本思想是：将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题，然后将这些子问题的解组合为原问题的解。

利用分治法可将快速排序的分为三步：

1、在数据集之中，选择一个元素作为”基准”（pivot）。
2、所有小于”基准”的元素，都移到”基准”的左边；所有大于”基准”的元素，都移到”基准”的右边。这个操作称为分区 (partition) 操作，分区操作结束后，基准元素所处的位置就是最终排序后它的位置。
3、对”基准”左边和右边的两个子集，不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

二、基本实现

2.1、基本思路

假设现在有以下待排序的数组：

i -> 0	1	2	3	4	5	j-> 6
7	8	9	1	6	2	9

上面的一栏表示索引，下面的一栏表示数值

1、首先，确定左索引指针为i = 0（之后简称为指针），右指针为j = 6，基数为base,首先可以确定基数为最左边的数，即base=7

2、排序开始时，j指针从右往左走，当指到小于等于基数的数时停下，即此时j=5;i指针从左往右走，找到大于等于基数的数时停下，即i=1

0	i -> 1	2	3	4	j-> 5	6
7	8	9	1	6	2	9

3、此时i,j两者的数值交换，即得如下

0	i -> 1	2	3	4	j-> 5	6
7	2	9	1	6	8	9

4、重复第2、3步，得

0	1	i -> 2	3	j->4	5	6
7	2	6	1	9	8	9

5、i、j指针相遇

0	1	2	i-> 3 <-j	4	5	6
7	2	6	1	9	8	9

6、i、j指针同时指向3索引，此时用i索引的位置去交换基准值

0	1	2	i-> 3 <-j	4	5	6
1	2	6	7	9	8	9

就这样，第一次排序即完成了，此时索引3左边的值都小于等于7，右边的值都大于等于7
7、分治递归
完成了以上之后，将7左边的数视为“左数组”，右边的数视为“右数组”，重复调用1~7步，直到数组中只含一个数为止，终止递归调用

0	1	2
1	2	6

4	5	6
9	8	9

2.2、代码实现

 public class QuickSortNormal {

    private static void quickSort(int[] a, int left, int right) {
        if (left >= right) return;

       int i = left + 1;
        int j = right;
        int base = a[left];

        while (true) {
            if (i >= j) break;
            if (i < j && a[j] >= base) {
                j--;
            } else if (i < j && a[i] <= base) {
                i++;
            }
            swap(a, i, j);
        }
        swap(a, left, i);
        quickSort(a, left, i - 1);
        quickSort(a, i + 1, right);
    }


    public static void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

三、优化快排

上一版的快排并不是最优化的快排，快排的平均复杂度O(nlogn)针对的是数据重复少且几乎无序的状态，有以下几个原因会让快排退化：

时间复杂度退化的原因
快排的平均时间复杂度为O(nlogn),这时在数据量较大且重复少、几乎无序的情况下。有两种情况会导致快排的时间复杂度退化到O(n^2):
1、数组近乎有序：

当数组近乎有序的时候，时间复杂度退化到O(n^2)，因为每次都取第一个元素作为基准的话，会出现无法均匀分割数组，从而使分割的数组变成链表状：

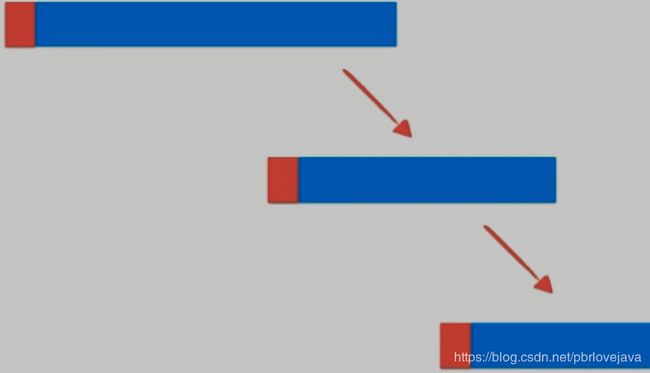
这时的解决办法是在数组中选取一个随机数作为基准，而不是取第一个数，这样子就能很好地避免在数组有序的情况下不能均匀切分数组的问题：

取随机数作为基准

public class QuickSortRandom {
    private static void quickSort(int[] a, int left, int right) {
        if (left >= right) return;

        //随机生成基准置于开头，解决近乎有序的数组排序时复杂度退化的问题
        int random = (int)(Math.random() * 1000 % (right - left) + left);
        swap(a, left, random);

        int i = left + 1;
        int j = right;
        int base = a[left];

        while (true) {
            if (i >= j) break;
            if (i < j && a[j] >= base) {
                j--;
            } else if (i < j && a[i] <= base) {
                i++;
            }
            swap(a, i, j);
        }
        swap(a, left, i);
        quickSort(a, left, i - 1);
        quickSort(a, i + 1, right);
    }


    public static void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

2、大数据量的数据重复：
当数组中的数据大量重复时，会出现分配不均匀问题切分不均匀问题，导致快排时间复杂度退化到O(n^2)

这时的解决办法有两个，第一个被称为双路快排,它的思想是将数组划分为小于等于基准和大于等于基准两部分，这样子在两部分中都拥有等于base的部分，不会出现两部分数据差很多：

双路快排

    public static void quickSort2Ways(int[] a,int left, int right) {
        if (left >= right) return;
        //随机生成基准置于开头，解决近乎有序的数组排序时复杂度退化的问题
        int random = (int)(Math.random() * 1000 % (right - left) + left);
        swap(a, left, random);
        int i = left + 1;
        int j = right;
        int base = a[left];
        while (true) {
            if (i >= j) break;
            if (i < j && a[i] < base) {
                i++;
            } else if (i < j && a[j] > base) {
                j--;
            }
            swap(a, i++, j--);
        }
        swap(a, left, j);
        quickSort2Ways(a, left, j - 1);
        quickSort2Ways(a, j + 1, right);
    }

    public static void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

还有一个思路非常常用，被称为三路快排，它的思想是将数组切分为三个部分：第一个部分小于baes，第二个部分等于base，第三个部分大于base，在下一次的迭代中，将小于base的部分继续排序，大于base的部分继续排序即可：

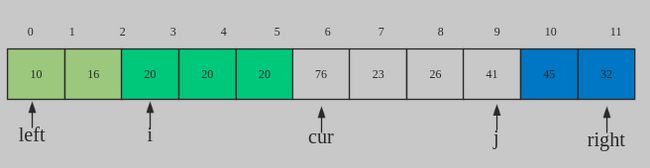
三路快排

public class QuickSort3Ways {
    public static void quickSort3Ways(int[] a, int left, int right) {
        if (left >= right) return;
        //随机生成基准
        int random = (int)(Math.random() * 1000 % (right - left) + left);
        int i = left + 1;//a[left...i)都小于base
        int cur = left + 1;//a[i...cur)都等于base
        int j = right;//a(j...right]都大于base
        int base = a[random];
        while (true) {
            if (cur >= j) break;
            if (i < j && a[cur] == base) {
                //当cur指向的元素等于base，则将cur往前指向，保持a[i...cur)都等于base
                cur++;
            } else if (i < j && a[cur] < base) {
                //当cur指向的元素小于base，则交换cur和i的值，并且cur和i都往前走一步，保持a[left...i)都小于base
                swap(a, i++, cur++);
            } else if (i < j && a[cur] > base) {
                //当cur指向的元素大于base，则交换cur和j的值，并且cur指向保持不变，因为cur仍指向一个未知的值，而j--保持a(j...right]都大于base
                swap(a, cur, j--);
            }
        }

        quickSort3Ways(a, left, i - 1);
        quickSort3Ways(a, j + 1, right);

    }


    public static void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

四、性能对比

先用一千万个范围在0~1000的数组进行排序对比普通快排和三路快排的速度：

   public static void main(String[] args) {
       //生成数据量
       int n = 10000000;
       int[] a = new int[n];
       //取值区间
       int k = 1000;
       for (int i = 0; i < n; i++) {
           a[i] = (int) (Math.random() * k);
       }

       long beginTime = new Date().getTime();

       QuickSortNormal.quickSort(a, 0, a.length - 1);

       long endTime = new Date().getTime();
       System.out.println("用时:" + (endTime - beginTime) + "毫秒"); quickSort(a, 0, a.length - 1);

   }

普通快排

三路快排

从实验结果可以看出，三路快排在千万级大重复数据量的情况下仍能在1s内进行排序，而普通快排花了27s，性能相差有27倍之多.