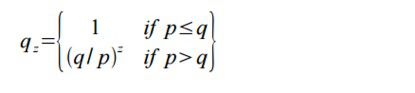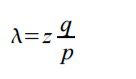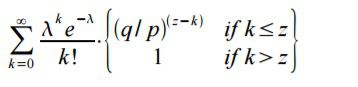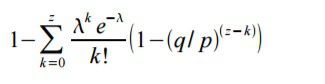《详解比特币白皮书》-Calculation (计算)

我们考虑如下场景，一个攻击者尝试生成另一条比诚实链增长更快的替代链。就算完成了这一步，系统也不会向随意的更改开放，比如无中生有创造价值，或者让攻击者拿到不属于自己的钱。节点是不会接受一个非法交易作为支付的，诚实节点也永远不会接受包含这些交易的区块。攻击者只能尝试去改变自己交易中的一个，来取回刚刚已经花出去的钱。

The race between the honest chain and an attacker chain can be characterized as a Binomial Random Walk.  The success event is the honest chain being extended by one block, increasing its lead by +1, and the failure event is the attacker's chain being extended by one block, reducing the gap by -1. 

诚实链与攻击者链之间的竞争可以表征为一个二项随机过程。成功事件是诚实链被延长了一个区块，领先+1，失败事件是攻击者链被延长了一个区块，差距-1。

The probability of an attacker catching up from a given deficit is analogous to a Gambler's Ruin problem.  Suppose a gambler with unlimited credit starts at a deficit and plays potentially an infinite number of trials to try to reach breakeven.  We can calculate the probability he ever reaches breakeven, or that an attacker ever catches up with the honest chain, as follows :

攻击者赶上一个给定亏损额（差距）的概率，类似一个赌徒破产问题。假设一个有着无限余额的赌徒，从一定亏损额开始，可能进行无限次试验，以达到盈亏平衡。我们可以计算他达到盈亏平衡，或者说攻击者追赶上诚实链的概率，如下：

p = probability an honest node finds the next block

诚实节点（率先）发现下一个区块的概率

q = probability the attacker finds the next block

攻击者（率先）发现下一个区块的概率

qz = probability the attacker will ever catch up from z blocks behind 

攻击者从落后z个区块的差距追赶上来的概率

Given our assumption that p > q, the probability drops exponentially as the number of blocks the attacker has to catch up with increases.  With the odds against him, if he doesn't make a lucky lunge forward early on, his chances become vanishingly small as he falls further behind. 

假设p > q，当攻击者需要追赶上的区块数量差距增长时，成功概率以指数方式下降。按攻击者的赔率，如果他没有率先完成一次幸运的冲抢，那么当他进一步落后的时候，机会将变得渺茫。

注：probability（概率）和odds（几率）是两个不同的数学概念。具体定义就不详述了，这里举个简单易懂的例子：不透明袋子里共有12颗球，其中红球3颗，剩下的是其他颜色。那么摸一颗红球出来的probability是3/12，通常按百分数表示为25%。

odds有两种表述形式，odds in favor和odds against。odds in favor描述“期望事件会发生”的比率，即所谓的胜率；odds against描述“期望事件不会发生”的比率，即赌博中常说的赔率。仍然是上面的例子，odds in favor摸红球是3/9，通常按比例表示为1:3；odds against摸红球是9/3，通常按比例表示为3:1。

另外，lunge一词在球类运动和动物世界中比较常见，意思是突然冲上去，往往带有进攻意图，或者要抢夺某种东西。作者接着race、odds这些双关语境，把攻击者追赶生成区块比喻为抢球。

We now consider how long the recipient of a new transaction needs to wait before being sufficiently certain the sender can't change the transaction.  We assume the sender is an attacker who wants to make the recipient believe he paid him for a while, then switch it to pay back to himself after some time has passed.  The receiver will be alerted when that happens, but the sender hopes it will be too late. 

我们现在来考虑一笔新的交易发生后，接收方需要等多久，才能足够确定发送方无法篡改交易。我们假设发送方是一个攻击者，他想要让接收方相信他已经暂时完成支付，然后过一段时间将交易转变为向自己支付。发送方那样做时接收方将会收到警告，但是发送方寄希望于这一切为时已晚。

The receiver generates a new key pair and gives the public key to the sender shortly before signing.  This prevents the sender from preparing a chain of blocks ahead of time by working on it continuously until he is lucky enough to get far enough ahead, then executing the transaction at that moment.  Once the transaction is sent, the dishonest sender starts working in secret on a parallel chain containing an alternate version of his transaction. 

接收方生成新的密钥对，并在签名之前将公钥交给发送方。这样避免了发送方提前准备好一条区块链，不断的在其上延长区块，直到他足够侥幸的超前足够远，然后在时机成熟时执行交易。一旦交易发出，不诚实的发送者开始秘密的在一条并行的链上进行运算，这条链包含了他的交易的另一（篡改）版本。

注：常听流行音乐的一定对alternate version不陌生。这个“另版”的范围很大，有时同样的歌曲会有多个版本，比如album version专辑版、cover翻唱版、remake重制版、clean干净版、explicit脏话版、instrumental伴奏版、acoustic演奏版、unplugged不插电版、live现场版、parody模仿版等等。

The recipient waits until the transaction has been added to a block and z blocks have been linked after it.  He doesn't know the exact amount of progress the attacker has made, but assuming the honest blocks took the average expected time per block, the attacker's potential progress will be a Poisson distribution with expected value: 

接收方会一直等到交易记录被追加到区块里，并且已有z个区块链接在其后。他并不知道攻击者已经取得的确切进展，但是假设诚实区块每产生一个将花费平均期望时间，那么攻击者可能取得的进展将是一个泊松分布，其期望值：

To get the probability the attacker could still catch up now, we multiply the Poisson density for each amount of progress he could have made by the probability he could catch up from that point:

现在为了得到攻击者仍然可能追赶上的概率，我们将攻击者每取得一定进展的泊松概率密度，乘以他从那一点开始能够追赶上的概率：

Rearranging to avoid summing the infinite tail of the distribution...

为了避免对分布的无穷长尾求和，化简为以下形式：

Converting to C code... 

转化为C语言代码：

Running some results, we can see the probability drop off exponentially with z. 

运行得出结果，可以看出随着z的增加，概率以指数形式下降。

Solving for P less than 0.1%... 

解出P少于0.1%的情况。