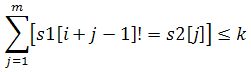-TEST Fin 2 for NOIP 最后准备(110-300)
头更更更大
这个11月完就要去搞NOIP了。。。
11月10天也就3次测试。。。为保佑进省一我还是每次测试玩都写个总结。。
emmm。。。
因为是最后一次测试所以为了给我们增长信心zgs给了我们一套真Day2题。

第一题没学过逆元,,精度上GG。
第二题瞎搞Floyed被反嘲讽了。。。。orz
第三题暴力60分(然而好像打得好可以变成正解)
于是就110。
这是考的题大家。。。看着就行。。。:
话说早睡早起身体好。。。
T1:回文数字(30/100)
problem:
题意:
有T个询问。每个询问一个数字n。
问你所有长度小于n的回文数字(不含前导零)的个数mod233333的值是多少。
样例:
输入:
6
0
1
2
3
4
5输出:
0
9
9
279
279
4779
solution:
本身是一个很简单的差比公式求和(不会的请参考高中数学(滑稽))
然而问题是a/b ≡ ?(mod d)不好求。
(考场上我是把a/b与d同时乘以b然后取模。。。也是做了个大死orz)
于是,我们要想办法解方程:
a/b ≡ a*c (mod d)(这里c就是逆元。)
转化得:b*c ≡ 1(mod d)
用欧几里得求解即可。
这里 x/9 ≡ x*25926 (mod 233333)
T2:路径统计(20/100)
problem:
题意:
一个 n 个点 m 条边的无重边无自环的无向图,点有点权,边有边权,定义一条路径的权值为路径经过的点权的最大值乘边权最大值。
求任意两点间的权值最小的路径的权值。
输入格式
第一行两个整数 n ,m ,分别表示无向图的点数和边数。
第二行 n 个正整数,第 i 个正整数表示点i的点权。
接下来 m 行每行三个正整数 ui,vi,wi ,分别描述一条边的两个端点和边权。
输出格式
输出 n 行,每行 n 个整数。
第 i 行第 j 个整数表示从 i 到 j 的路径的最小权值;如果从 i 不能到达 j ,则该值为 -1 。特别地,当 i=j 时输出 0 。
样例:
输入
3 3
2 3 3
1 2 2
2 3 3
1 3 1输出
0 6 3
6 0 6
3 6 0
solution:
如果没有点权这道题就是一个Floyed完事。(n,m<=500)
转移:
f[i][j]=min(f[i][j],max(f[i][k],f[k][j]));有点权之后就把所有的点按从小到大的顺序排序,对点权重复如上操作,然后更新答案。
转移:
//(初始化:g[i][j]=INF;f[i][j]=INF;g->点权;f->答案)
g[i][j]=min(g[i][j],max(g[i][k],g[k][j]));
if(i<=k&&j<=k)//保证当前路径的点权一定是整个路径中最大的 f[i][j]=min(f[i][j],val[k]*g[i][j]);T3:字符串(60/100)
problem:
题目描述
给定两个字符串 s1 和 s2 ,两个字符串都由 26 个小写字母中的部分字母构成。现在需要统计 s2 在 s1 中出现了的次数。
对于 s1 中的每个位置 i ,设 strlen(s2)=m ,若:
(最外层中括号为布尔表达式)
则认为 s2 在 s1 的 i 处出现了一次,现在想知道,s2 在 s1 中一共出现了多少次?
输入格式
第一行为一个字符串 s1 ;
第二行为一个字符串 s2 ;
第三行为一个整数 k 。
输出格式
输出一行一个整数,表示 s2 在 s1 中出现的次数。
样例数据
输入
ababbab
aba
1输出
3
solution:
暴力求解即可。(打得好,有高超的卡常技巧就能水过)
正解是后缀数组加RMQ。。。。。。

感想:
多练模板!!!多记Dp套路!!!多复习!!!
代码:
T1:
my/std.cpp:
#includeT2:
my/std.cpp:
#includeint pos[505],vae[505];
const long long INF=2e18;
int n,m,u,v,val;
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++){dot[i].val=read();dot[i].pos=i;}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
f[i][j]=2e9;ans[i][j]=INF;
}
for(int i=1;i<=m;i++)
{
u=read();v=read();val=read();
f[u][v]=val;f[v][u]=val;
}
sort(dot+1,dot+n+1,comp);
for(int i=1;i<=n;i++)
{
pos[i]=dot[i].pos;
vae[i]=dot[i].val;
f[i][i]=0;ans[i][i]=0;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
f[pos[i]][pos[j]] = min(f[pos[i]][pos[j]],max(f[pos[i]][pos[k]],f[pos[k]][pos[j]]));
if(i<=k&&j<=k)
ans[pos[i]][pos[j]] = min(ans[pos[i]][pos[j]],1LL*vae[k]*f[pos[i]][pos[j]]);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(ans[i][j]==INF)cout<<"-1 ";
else cout<" ";
}
cout<return 0;
} T3:
my/std.cpp:
#pragma GCC optimize("O2")//考试时千万别用,不信的可以试试。(滑稽)
#includereturn 0;
}