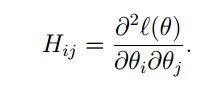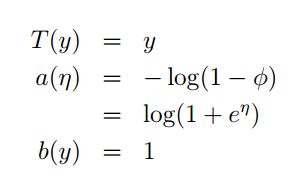监督学习之广义线性模型——Andrew Ng机器学习笔记（三）

内容提要

这篇博客的主要内容有
- 牛顿法
- 指数分布族（Exponential Family）
- 广义线性模型（Generalized Linear Models）
- Softmax Regression

牛顿法

首先我们先看一个简单的例子。
定义函数 f:R→R ，自变量为 θ 。我们现在找一个 θ 使得 f(θ)=0 。
牛顿法的思想就是利用一阶导数的定义，得到 θ 的迭代关系。如下图示意：

根据导数的定义，我们就可以得到：

f′(θ(1))=f(θ(1))/ΔΔ=f(θ(1))/f′(θ(1))θ(2)=θ(1)−Δ

从而我们就可以得到一般的迭代公式：

θ(k+1)=θ(k)−Δ其中Δ=f(θ(k))/f′(θ(k))

回顾前面的对数似然函数，我们都是要求它的最大值，即就是要寻找一个参数 θ 使得对数似然函数的导数为零，即 l′(θ)=0
- 当 θ 为一维向量时，我们利用牛顿法的思想可以得到更新规则为：

θ:=θ−l′(θ)/l′′(θ)

因为我们举得例子是对函数零阶导时为0，求参数。这里我们是函数一阶导数的情况，用同样的思想将式子中对应的量替换掉就可以了。
- 当 θ 为一个大于一维的向量时，我们得到的迭代规则为：

其中 H 为Hessian矩阵：

你也可以参看最优化的教程，就会发现，牛顿法一般只需要一部迭代就可以得到最优解。但是牛顿法最大的问题就是Hessian矩阵的逆，并不是总可以得到，或者逆求逆的计算量非常大，最优化中有一章专门就是解决这个问题。解决的基本思路就是用一个矩阵 B 去近似Hessian矩阵。

指数分布族（Exponential Family）

族的概念在高等数学中就有。我们这里的指数分布族，和之前的所讲的族的概念是一样的。下来我们首先看看指数分布族的一般表达式：

其中
- η 为自然参数（natural parameter or canonical parameter）
- T(y) 为充分统计量（sufficient statistic），一般情况下， T(y)=y
- 当给定 a,b,T;η为参数 时就可以得到一个确定的分布

事实上我们之前说过的逻辑回归就是指数分布族的特例。还有伯努利分布 P(y=1;ϕ)=1 ，正态分布都是指数分布族的特例。除此之外还有很多。

下面我们来说明为什么伯努利分布，高斯分布是指数分布族的特例。其实就是给出这些特例分布对应的 a,b,T

伯努利分布

当 y∈0,1 时，可以如下的方式表达：

利用逻辑回归同样的思想，可以将表达式进行如下简写，同时向指数分布族的样子凑：

凑完之后，我们根据指数分布族的样子就可以在式子中找到 a,b,T ：

同时我们还可以得到 η和ϕ 之间的关系：

这样我们就可以利用参数 η 来表示指数分布族中的 a,b,T 了，这就是上面式子中 a(η)=log(1+eη) 的原因，同时这也说明了伯努利分布是指数分布族的一个特例。下面我们来看高斯分布。

高斯分布

我们之前推导最小二乘回归的时候发现 σ2 其实不重要，如下：

我们最终利用求目标函数极值的方法去求解参数 θ 。这里可以看到与 σ 没有多大关系。所以我们可以令 σ2=1

利用和伯努利分布同样的思想，可以得到下面的式子：

再和指数分布族的通式进行比对，就会得到相应 a,b,T ：

多元高斯分布也是指数分布族的特例。同样泊松分布也是，指数分布就更不用说。

广义线性模型（Generalized Linear Models（GLM））

在这一部分我想说明如何利用指数分布族。首先我们先做如下的假设：
1. y|x;θ∼ExpFamily(η) ，这个式子的理解是：在确定 x 输入并有特征 θ 的情况下， y 服从自然参数 η 的指数分布族。一般， η 有 x和θ 确定。
2. 给定 x ，估计函数定义为： h(x)=E[T(y)|x;θ] ，一般 T(y)=y
3. η=θTx ，如果 η 是向量则： ηi=θTx

在假设一中（ y|x;θ∼ExpFamily(η) ），先取一个特例：伯努利分布，它的参数为 ϕ ,然后估计函数(响应函数)就可以写成： hθ(x)=E(y|x;θ)=P(y=1|x:θ)=ϕ ，其中用到了伯努利分布的期望，它的期望就等于事件发生的概率，即参数 ϕ 。我们上面有伯努利分布的指数分布的表达形式，可以知道 ϕ=(1+e−η)−1 ，最终就可以得到 hθ(x)=(1+e−θTx)−1

术语介绍：
g(η)=E[y|η]=(1+e−η)−1 ，这称之为：正则响应函数
g(η)−1 ，称为：正则关联函数

另外一个特例：输入值 x∼N(μ,σ2) ，我们让 μ=η ,可以得到响应函数如下关系：

多项式分布

前面我们说过逻辑回归，其中讲的例子是一个二元分类，但是实际当中往往是多元分类问题。

那么 y∈{0,1} 就无法满足要求，下来我们就看一个 y∈{1,2...k} 的问题。
给定参数 ϕ1,ϕ2...ϕk ,即 y 取某一个值时的概率。利用概率的基本知识就可以得到：

在这里 T(y)≠y 而是 T(y)∈Rk−1 ，一般做如下定义：

指示器函数 1{true}=1;1{false}=0 ，利用指示器函数我们可以对 T(y) 进行简写： (T(y)i)=1{y=i}

其实对于每一个 y 的取值，就可以看成是一个伯努利分布。所以可以得到下面的表达：

同样的我们将 y 的分布向指数分布族靠近：

其中：

和前面的一样， η和ϕ 之间存在着函数关系：

就可以做如下推导：

就可以得到：

再根据（1）式就可以得到：

那么 y 的概率表达式就可以改写成：

Softmax Regression

根据上面的推导我们就可以介绍Softmax Regression了。对于一个分类问题， y∈{1,2...k} ,当 η=θTx 时，响应函数为：

特别的 E[y=k|x;θ]=P(y=k|x;θ)=1−∑k−1i=1ϕi

如果我们的训练集大小为 m ： {(x(i),y(i));i=1,2...m} ，我们写出对应的对数似然函数：

上面的式子是Andrew Ng老师给的，我自己进行了下面的推导：

有似然函数的梯度之后，我们就可以利用梯度上升的方式去迭代 θ 了。
可以看出Softmax Regression是对逻辑回归的推广，可以处理多元分类问题。Sortmax Regression就是一个广义线性模型的算法。我自己理解的，为什么这种算法会被列为广义线性模型的例子，原因是，对于每一个 η=θTx 这是线性的，但是整体而言又是伯努利分布。广义的原因就是在线性的外面套了一层，线性已经不是单纯的线性了。

end