经典排序算法之插入排序 C++

插入排序（Insertion Sort）

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的基本操作是将一个记录插入到已经排好序的有序表。

1.直接插入排序(Straight Insertion Sort)

1.1 算法描述

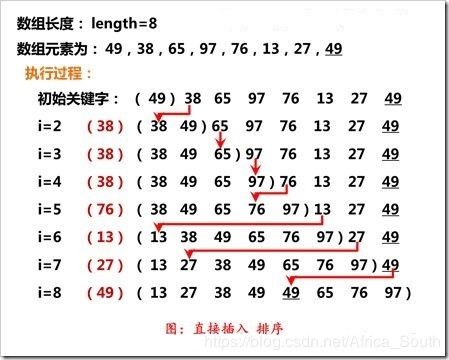
一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

• 1.从第一个元素开始，该元素可以认为已经被排序；
• 2.取出下一个元素，在已经排序的元素序列中从后向前扫描；
• 3.如果该元素（已排序）大于新元素，将该元素移到下一位置；
• 4.重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
• 5.将新元素插入到该位置后；
• 6.重复步骤2~5。
  

1.2 复杂度

• 时间复杂度O($n^2$)
• 空间复杂度O(1)

1.3 代码实现

#include
#include

using namespace std;

/*对49,38,65,97,76,13,27,49共8个元素进行直接插入排序*/

// 将arr[0]设置为哨兵,不参与排序,length为排序个数
// 对arr[1,2,...,length]进行排序
void InsertSort1(int* arr, int length) {
	for (int i = 2; i <= length; i++) {
		if (arr[i] < arr[i - 1]) {
			arr[0] = arr[i]; // 将arr[0]设置为哨兵
			arr[i] = arr[i - 1];
			int j;
			for (j = i - 2; arr[j] > arr[0]; j--) {
				arr[j + 1] = arr[j]; // 将大的，往后移动
			}	
			arr[j + 1] = arr[0]; // 将arr[i]放在正确的位置
		}
	}
}
// 为arr[0,1,...,length-1]排序
void InsertSort2(int* arr, int length) { 
	for (int i = 1; i < length; i++) {// arr[0]也参与排序
		int tmp = arr[i];
		int j;
		for (j = i - 1; j >= 0 && arr[j] > tmp; j--) arr[j + 1] = arr[j]; // 将大的，往后移动
		arr[j + 1] = tmp;
	}
}

// 打印数组arr[start,...,end]
void printArr(int* arr,int start,int end) {
	for (int i = start; i <= end; i++) cout << arr[i]<<" ";
	cout << endl;
}
int main() {
	int arr1[9] = { 0,49,38,65,97,76,13,27,49 };
	InsertSort1(arr1, 8);
	printArr(arr1, 1, 8);

	int arr2[8] = { 49,38,65,97,76,13,27,49 };
	InsertSort2(arr2, 8);
	printArr(arr2, 0, 7);

	system("pause");
	return 0;
}

2.折半插入排序(Binary Insertion Sort)

因为插入排序的基本操作是在一个有序表中进行查找和插入,所以查找操作可以利用折半查找操作来实现。

#include
#include

using namespace std;

/*对52,38,65,97,76,13,27,49共8个元素进行折半插入排序*/
//折半插入排序
//为arr[0,1,...,length-1]排序 
void BInsertSort(int* arr, int length) {
	for (int i = 1; i < length; i++) {
		int temp = arr[i];
		int low = 0;
		int high = i - 1;
		//注意,为什么我要用=号,因为如果是下列这种情况
		//38，52插入62,则插在high后面;
		//38,52,65插入52,则插在high处。
		while (low <= high)							//在arr[low,high]中折半查找有序插入的位置
		{
			int mid = (low + high) / 2;					//折半
			if (arr[mid] > temp) high = mid - 1;	//插入点在低半区
			else low = mid + 1;//插入点在高半区
		}
		for (int j = i - 1; j >= high+1; j--) arr[j + 1] = arr[j];
		arr[high+1] = temp;
	}
}
//打印数组arr[start,...,end]
void printArr(int* arr, int start, int end) {
	for (int i = start; i <= end; i++) cout << arr[i] << " ";
	cout << endl;
}

int main() {
	int arr3[8] = { 52,38,65,97,76,13,27,49 };
	BInsertSort(arr3, 8);
	printArr(arr3, 0, 7);

	system("pause");
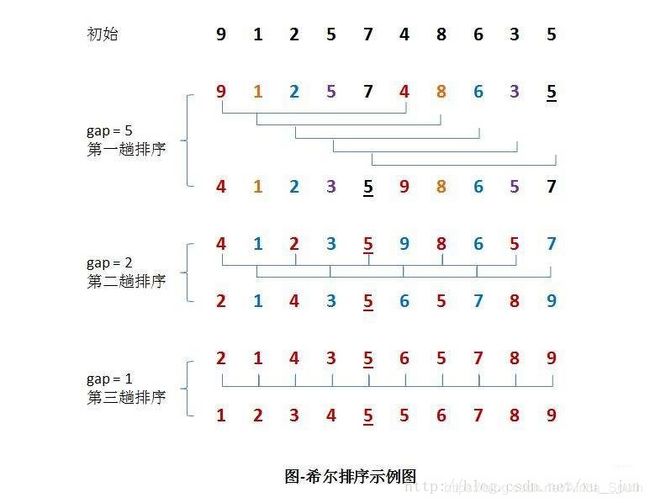
	return 0;
}

3.希尔排序(Shell Sort)

希尔排序又称"缩小增量排序"(Diminishing Increment Sort)，是第一批突破O($n^2$)的排序算法之一,是直接插入排序的改进。
由对直接插入排序分析可知,若待排记录序列为“正序”时，其时间复杂度可以提高到O(n)。所以,我们的想法是使得待排记录逐渐基本有序,直接插入排序的效率就能提高。

3.1 算法基本思想

先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录基本有序时，再对全体记录进行一次直接插入排序。

3.2 算法流程

• 选择一个增量序列$t_1，t_2，\dots ，t_k$，其中$t_i>t_j(i>j)，t_k=1$；
• 按增量序列个数k，对序列进行k 趟排序；
• 每趟排序，根据对应的增量$t_i$，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。

子序列的构成不是简单的“逐段分割”，而是将相隔某个“增量”的记录组成一个子序列。

3.3 算法复杂程度

• 时间复杂度：O($n^{1.3}$)
  希尔排序的时间是所取增量序列的函数,涉及到一些数学上尚未解决的难题。当n在某个特定的范围内,时间复杂度约为O($n^{1.3}$)。
• 空间复杂度：O(1)

3.4 代码实现

风格1：通用格式

#include
#include

using namespace std;

/*对49，38，65，97，76，13，27，49，55，04共10个元素进行希尔排序*/

//打印数组arr[start,...,end]
void printArr(int* arr, int start, int end) {
	for (int i = start; i <= end; i++) cout << arr[i] << " ";
	cout << endl;
}
//对顺序表arr[]进行希尔排序
/* * 对顺序表arr[]做一趟希尔插入排序 * 与直接插入排序的区别: * 前后记录位置的增量为dk，而不是1 */
void ShellInsert(int* arr, int dk,int length) {
	for (int i = 0 + dk; i < length; i++) {
		int temp = arr[i];
		int j;
		for (j = i - dk; j >= 0 && arr[j] > temp; j -= dk) arr[j + dk] = arr[j];
		arr[j + dk] = temp;
	}
}
//dlta[0...t-1]是增量序列,length是顺序表arr的长度
void ShellSort(int* arr, int* dlta, int t,int length) {
	for (int i = 0; i < t; i++) ShellInsert(arr, dlta[i],length); //一趟增量为dlta[i]的插入排序
}
int main() {
	int arr[10] = { 49,38,65,97,76,13,27,49,55,04 };
	int length = 10;
	int dlta[] = { 5,2,1 };
	ShellSort(arr, dlta, 3,10);
	printArr(arr, 0, 9);

	system("pause");
	return 0;
}

风格2：
从列表长度开始,每趟希尔插入排序的增量都是上一次增量除以2，直到增量为1

#include
#include

using namespace std;

/*对49，38，65，97，76，13，27，49，55，04共10个元素进行希尔排序*/

//打印数组arr[start,...,end]
void printArr(int* arr, int start, int end) {
	for (int i = start; i <= end; i++) cout << arr[i] << " ";
	cout << endl;
}
//对顺序表arr[]进行希尔排序
//n为列表长度,以n为初项,1/2为公比的等比数列为增量序列,且终止于1
void ShellSort(int* arr, int length) {
	int i, j, temp, increament;
	for (increament = length / 2; increament > 0; increament /= 2) {
		for (i = 0 + increament; i < length; i++) {
			temp = arr[i];
			for (j = i - increament; j >= 0 && arr[j] > temp; j -= increament) 
				arr[j + increament] = arr[j];
			arr[j + increament] = temp;
		}
	}
}
int main() {
	int arr[10] = { 49,38,65,97,76,13,27,49,55,04 };
	int length = 10;
	ShellSort(arr,10);
	printArr(arr, 0, 9);

	system("pause");
	return 0;
}

参考资料

1.严蔚敏 吴伟民.《数据结构》(C语言版)。
2.十大经典排序算法(动态演示)
https://www.cnblogs.com/onepixel/articles/7674659.html