hihocoder1032:最长回文字串

题意：

就是给你一个字符串：让你在字符串中找到它的最大的回文字串。

思路：

这道题学到了一个新的算法，manacher求最长回文字串的算法。
首先推荐一个博客[这篇文章是我见过的讲解的最清楚的文章了,推荐给大家]
Manacher算法:
首先我们设置p[i]表示以i为中心的回文串的长度，假设现在扫描到了i+k这个位置，那么maxlen代表的就是在(i+k)之前的所有回文串中所能延伸到的最右端的位置。即maxlen=max(maxlen,p[i]+i);

然后接下来我们分2种大情况讨论这个问题：
1.当(i+k)这个位置不在前面的任何回文串中，即i+k>maxlen，那么p[i+k]=1，然后让i+k往左右两边继续延伸，即为：

while(s[i+k+p[i+k]]==s[i+k-p[i+k]]) ++p[i+k];

2.当(i+k)这个位置被前面的字符串所包含：
- (i-k)回文串有一部分是在i的回文串半径之外。

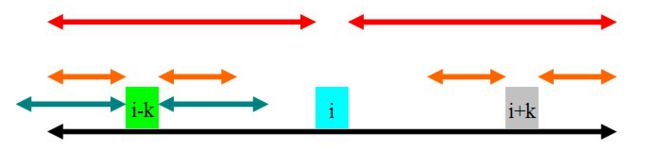
那么我们能够得到的i+k的最大回文半径为围绕在i-k的那个橙色的那段，因为i的回文半径已经确定了，所以i+k的回文半径是不可能比橙色的那段更大的，因为如果增大的话，那么i的回文半径也就会跟着增大，而i是在i+k之前就已经被判断过的，所以矛盾，所以i+k的回文半径就是橙色这么大。（如下图所示）

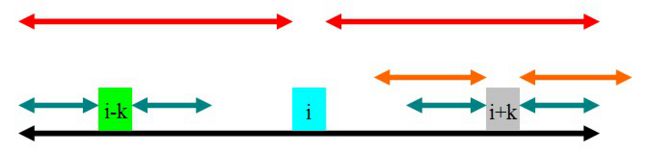
- (i-k)回文串没有超过i的回文半径之外。

那么i+k的回文半径只可能是与i-k同样长的，因为i+k是和i-k相对应的，所以如果i+k增大，则i-k也会相应增长。而i-k是之前就已经判断好了的。
所以矛盾。（如下图所示）

- 当i-k的半径刚好与i的回文半径的最左边相重合时，那么i+k的最小能够保证的回文半径是和i-k一样长。但是因为i-k的最左端和i+k的最右端是不一样的，虽然i-k的回文半径是被限制了，但是i+k的回文半径还是可以被增长的。
注意这里要和第二大类的第一种情况相区分

然后把上面两种情况总结一下就是：

//注意这里i就是我们所遍历到的位置了（与上面的那个id要区别一下）
p[i]=min(p[id-(i-id)],p[id]-(i-id))
while(s[i+p[i]]==s[i-p[i]]) ++p[i];

然后还剩下最后一个问题了：
就是我们要把偶数长度的字符串插入’#’从而使它们变成奇数长度的字符串，这样我们才能够找到中心。
无论字符串是以’#’为中心还是以字母为中心展开的最长回文字串，它肯定都是以’#’结束的。然后找规律可以得到：最长回文字串的长度肯定是最长的回文字串半径的长度减去1。（这个我也不好证明，如果有谁能够提供证明的话那就非常感谢啦~~总之要理解的话可以通过找规律的方式嘛，自己列几个例子就知道了）

Code：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
#define inf 99999999
#define maxn 1000010
char a[maxn*3];
int p[maxn*3];
int main(){
    int N;
    scanf("%d",&N);
    while(N--){
        int id=0,maxlen=0;
        scanf("%s",a);
        int len=strlen(a);
        memset(p,0,sizeof(p));
        for(int i=len-1;i>=0;i--){
            a[2*(i+1)]='#';
            a[2*(i+1)-1]=a[i];
        }
        a[0]='#'; a[len*2+1]='\0';  //这里不要忘记给开头和结尾都赋上值！
        //printf("%s\n",a);
        for(int i=0;i2+1;i++){
            if(id+p[id]>i) p[i]=min(p[2*id-i],p[id]-(i-id));
            else p[i]=1;
            //最重要的是在下面，你要注意防止越界，所以你要加上条件才行！！！
            while(a[i+p[i]]==a[i-p[i]]&&i-p[i]>=0&&i+p[i]2+1) p[i]++;
            if(i+p[i]>id+p[id]) id=i;
            if(maxlenprintf("%d\n",maxlen-1);
    }
    return 0;
}