CCF-201803-4-棋局评估

终于做了这道题，看网上说的是要用博弈论的人工智能的算法----对抗搜索，极大极小值算法。

这个算法大概意思就是，定义一种得分情况，然后给每个局势定义一个得分，正数表示先手有利的，负数表示后手有利的，每次博弈，找最有利于自己的情况。对于先手来说，每次找所有可下棋位置的分值的最大值，后手就是最小值。

这道题来说，深搜递归遍历所有出现的棋局，计算所有棋局的分值。复杂度为 9！，不大，可以直接暴力搜索所有棋局。

胜利情况很好判断，棋盘为3*3的棋盘，可以用1-9序号表示每个位置，3子相连的时候，相邻序号差都相等。比如0-1-2相连，0-3-6相连，0-4-8相连。或者，胜利情况只有8种横三种，竖三种加两条对角线，直接判断这8种情况是否有相连。

设搜索函数为dfs(i), i=先后手玩家，1先手，2后手。
每次dfs(i)，i == 1时找最大值，i == 2时找最小值。

题解大概流程：
深搜模拟下棋，找可以下的格子下，更新最大最小值。然后重复流程，直到下满或已分出胜负。

优化：
1.记忆化搜索：把前面的棋局记下来，下次遇到同样的棋局就不用搜，直接在映射表里面找。下个样例就可以用上个样例留下来的映射表。

记忆化搜索版本

import sys

sys.setrecursionlimit(10 ** 7)


# 数空格子个数
def count_space(board):
    cnt = 0
    for e in board:
        if e == 0:
            cnt += 1
    return cnt


# 分胜负，先手胜返回正分，后手胜返回负分，未分出胜负返回0
def win(board):
    # 行判断
    for idx in [0, 3, 6]:
        if board[idx] == board[idx + 1] == board[idx + 2] == 1:
            return count_space(board) + 1
        elif board[idx] == board[idx + 1] == board[idx + 2] == 2:
            return -(count_space(board) + 1)

    # 列判断
    for idx in [0, 1, 2]:
        if board[idx] == board[idx + 3] == board[idx + 6] == 1:
            return count_space(board) + 1
        elif board[idx] == board[idx + 3] == board[idx + 6] == 2:
            return -(count_space(board) + 1)

    # 对角线判断
    if board[0] == board[4] == board[8] == 1 or board[2] == board[4] == board[6] == 1:
        return count_space(board) + 1
    elif board[0] == board[4] == board[8] == 2 or board[2] == board[4] == board[6] == 2:
        return -(count_space(board) + 1)
    return 0


# 博弈树深搜
def dfs(board, player):
    judge = win(board)
    if judge:
        return judge
    else:
        min_score, max_score = 99999999999, -9999999999
        for i in range(9):
            if board[i] == 0:
                new_board = board[:]
                new_board[i] = player
                score = d[str(new_board)] if str(new_board) in d else dfs(new_board, 1 if player == 2 else 2)
                d[str(new_board)] = score
                min_score = score if score < min_score else min_score
                max_score = score if score > max_score else max_score
        # 棋盘下满，因为此时没胜负，返回0
        if count_space(board) == 0:
            return 0
        # 否则返回最大值或最小值
        return min_score if player == 2 else max_score


d = {}  # 映射表 k：棋局 v：分数
t = int(input())
for i in range(t):
    board = []  # 棋盘
    for j in range(3):
        for e in input().split():
            board.append(int(e))
    print(dfs(board, 1))

2.Alpha-Beta剪枝：看图理解

每一层表示第几步，1表示先手，2表示后手

经过第三层找到第二层第一个最小值5，随后就更新第一层的最大值为5。

然后又通过第三层的4和5更新第二层第二个最小值为4，因为这个最小值只会越更新越小，而上一层是要找最大值，而4<5, 已经小于上一层的最大值，不会对上一层的5有影响，不用再继续找了，就相当于剪掉没用的枝干了。如图圈住叉掉部分。

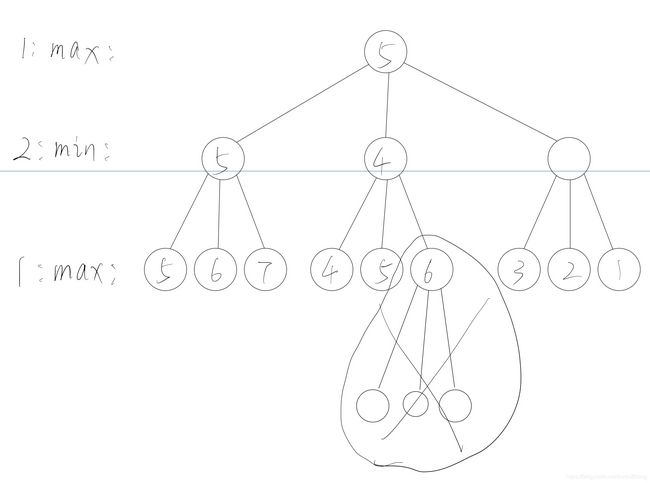
同理第二层右边的3也剪掉了一部分枝干

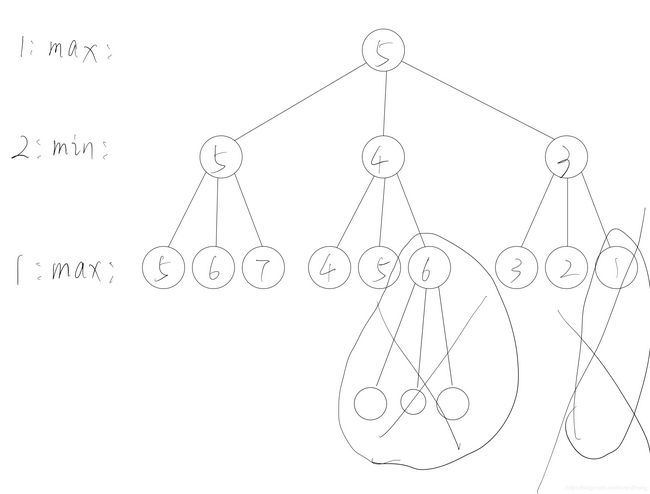
剪枝版本代码

import sys

sys.setrecursionlimit(10 ** 7)


def count_space(board):
    cnt = 0
    for e in board:
        if e == 0:
            cnt += 1
    return cnt


def win(board):
    # 行判断
    for idx in [0, 3, 6]:
        if board[idx] == board[idx + 1] == board[idx + 2] == 1:
            return count_space(board) + 1
        elif board[idx] == board[idx + 1] == board[idx + 2] == 2:
            return -(count_space(board) + 1)

    # 列判断
    for idx in [0, 1, 2]:
        if board[idx] == board[idx + 3] == board[idx + 6] == 1:
            return count_space(board) + 1
        elif board[idx] == board[idx + 3] == board[idx + 6] == 2:
            return -(count_space(board) + 1)

    # 对角线判断
    if board[0] == board[4] == board[8] == 1 or board[2] == board[4] == board[6] == 1:
        return count_space(board) + 1
    elif board[0] == board[4] == board[8] == 2 or board[2] == board[4] == board[6] == 2:
        return -(count_space(board) + 1)
    return 0


# 博弈树深搜
def dfs(board, player, pre):
    judge = win(board)
    if judge:
        return judge
    else:
        min_score, max_score = 999999999, -9999999999
        for i in range(9):
            if board[i] == 0:
                new_board = board[:]
                new_board[i] = player
                score = 0
                if player == 1:
                    score = dfs(new_board, 1 if player == 2 else 2, max_score)
                elif player == 2:
                    score = dfs(new_board, 1 if player == 2 else 2, min_score)

                # 当前为先手，得分要比上一轮小，否则剪枝
                if player == 1 and score >= pre:
                    return score
                # 同理
                elif player == 2 and score <= pre:
                    return score

                min_score = score if score < min_score else min_score
                max_score = score if score > max_score else max_score

        # 棋盘下满，因为此时没胜负，返回0
        if count_space(board) == 0:
            return 0
        # 否则返回最大值或最小值
        return min_score if player == 2 else max_score


t = int(input())
for i in range(t):
    board = []  # 棋盘
    for j in range(3):
        for e in input().split():
            board.append(int(e))
    print(dfs(board, 1, 99999999))

小结：对于这种零和博弈，对我方有利，就一定对对手不利。所以先手每次选最大值的地方下，必然于对手不利。