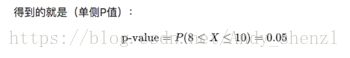统计学基础--假设检验
假设检验
1、假设检验的由来
我们先看一个例子:
那么如何检验这位女士的说法呢?FISHER进行了研究,从而提出了假设检验的思想。
比如:
正常情况下我们去猜先倒茶还是先倒牛奶的话,概率应该是1/2,
1.总共检验了两杯,全部猜对的概率是:0.5✖️0.5=0.25,虽然概率很低,但是也算正常;
2.继续猜,又猜了两次,也全部猜对了几率是![]() =0.0625,这个概率明显是非常低了,有点不正常了,但是会不会还是运气呢?
=0.0625,这个概率明显是非常低了,有点不正常了,但是会不会还是运气呢?
3.我们继续猜,加大样本,如果连续猜对10杯,那么我认为这位女士确实有特殊的能力。
虽然我们上面说猜对10杯来确认这位女士有特殊能力,这只是我们的臆测,我们假设一个x,当这位女士能够猜对x杯才认为这位女士确实有特殊的能力,其实对于我们最难的是来确认着x。
下面我们就来看一下怎么样来确认这个x。
2、什么是假设检验
假设检验(Hypothesis Testing):是推断统计的最后一步,是依据一定的假设条件由样本推断总体的一种方法。
你提出你的假设:说你有特殊的能力,可以品出先倒茶还是牛奶;
我提出要检验你的假设:品十(x)杯,看实验结果是不是和你说的假设相符
假设检验的基本思想是小概率反证法思想,小概率思想认为小概率事件在一次试验中基本上不可能发生,在这个方法下,我们首先对总体作出一个假设,这个假设大概率会成立,如果在一次试验中,试验结果和原假设相背离,也就是小概率事件竟然发生了,那我们就有理由怀疑原假设的真实性,从而拒绝这一假设。
假设检验其实就是假设和检验两步,先提出假设,之后再来验证假设是不是合理的。
3、P值
为了完成假设检验,需要先定义一个概念:P值。
根据上面的描述,这里假设检验的思路就是:
假设:这位女士不能准确的猜出先倒茶还是牛奶(没有确凿证据一般不推翻的假设,正常情况下我们都不能猜出先倒茶还是牛奶,所以我们假设这位女士不能准确的猜出先倒茶还是牛奶)
检验:认为假设是成立的,然后猜十次,看结果与假设是否相符
猜奶茶的实验应该符合二项分布(这就不解释了),也就是:
X~(n,
) 其中,n代表猜的次数,u代表猜对的概率。
在我们认为猜之前没有泄密(也就是确实是凭自己的嗅觉去猜)的前提下,猜10次应该符合以下分布:
X~(10,0.5)
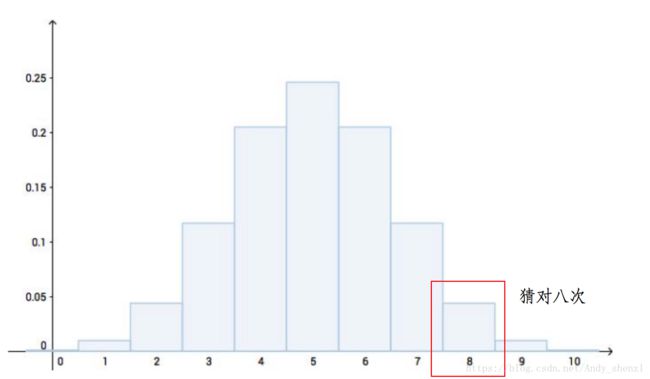
下图表示的就是,假如猜是公平的情况下的分布图:
P=
* (
)* (
) =0.0439
也就是说猜10次能猜对8次的概率是0.0439
为了方便大家计算,附上python代码:
import operator
from functools import reduce
def c(n,k):
return reduce(operator.mul, range(n - k + 1, n + 1)) /reduce(operator.mul, range(1, k +1))
def fac(n):
return reduce(operator.mul, range(1,n+1))
print (c(10,8))
print (fac(5))
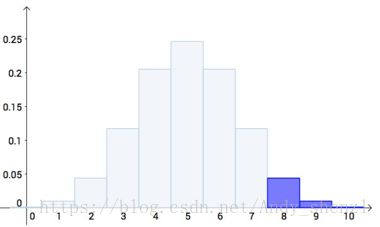
把八次猜对概率,与更极端的九次猜对、十次猜对的概率加起来:
为什么要把更极端的情况加起来?
根据猜奶茶这个例子,可能你会觉得,我知道八次猜对出现不正常就行了,干嘛要把九次、十次加起来?
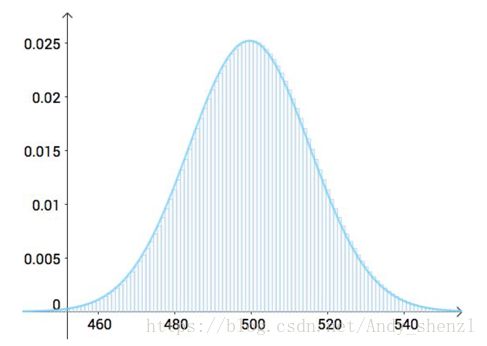
比如我们要猜1000次用二项分布来计算很麻烦,根据中心极限定理,我们知道,可以用正态分布来近似:
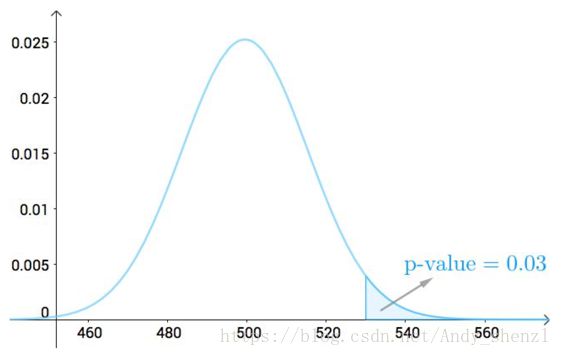
但是,对于正态分布,我没有办法算单点的概率(连续分布单点概率为0),我只能取一个区间来算极限,所以就取530、以及更极端的点组成的区间:
(我上面只取了单侧P值,说明下:取单侧还是双侧,取决于你的应用,什么叫做更极端的点,也取决于你的应用)
3.1、单侧检验
-
当关键词有不得少于/低于的时候用左侧,比如灯泡的使用寿命不得少于/低于700小时时
当关键词有不得多于/高于的时候用右侧,比如次品率不得多于/高于5%时
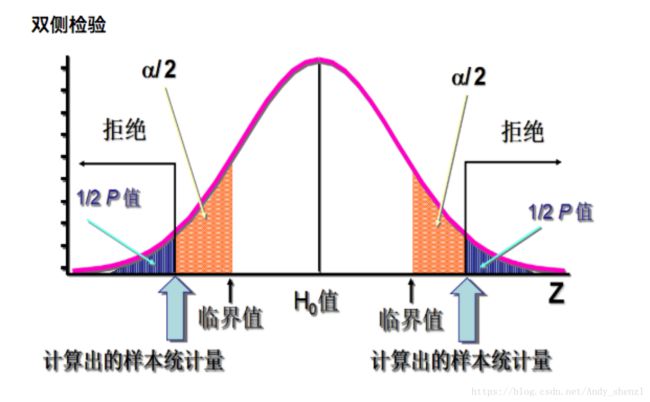
3.2 双侧检验
单侧检验指按分布的一侧计算显著性水平概率的检验。用于检验大于、小于、高于、低于、优于、劣于等有确定性大小关系的假设检验问题。这类问题的确定是有一定的理论依据的。假设检验写作:μ1<μ2或μ1>μ2。
双侧检验指按分布两端计算显著性水平概率的检验, 应用于理论上不能确定两个总体一个一定比另一个大或小的假设检验。一般假设检验写作H1:μ1≠μ2。
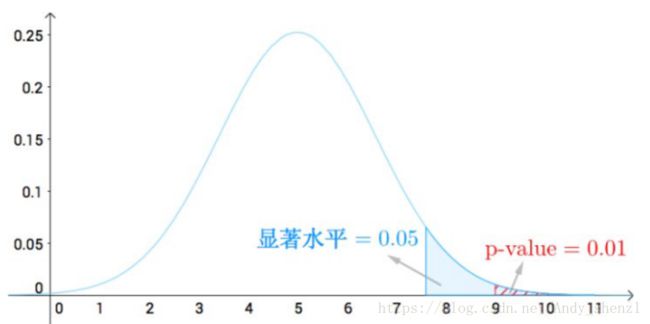
4、显著水平
总共猜10次,那么是出现7次猜对,可以认为有特殊能力,还是9次猜对之后我才能确认有特殊能力,这是一个较为主观的标准。
我们一般认为
P-value<=0.05
就可以认为假设是不正确的。
0.05这个标准就是显著水平,当然选择多少作为显著水平也是主观的。
比如,我们猜奶茶的例子,如果取单侧P值,那么根据我们的计算,如果10次猜对9次:
P-value=P(9<=X<=10)=0.01<=0.05
我们可以认为刚开始的假设(这位女士不能准确的猜出先倒茶还是牛奶)错的很“显著”,也就是是有特殊能力的。
5、假设检验步骤
我们回顾下我们刚才所说的,总结下:
这里简单说下检验统计量
检验统计量是用于假设检验计算的统计量。在零假设情况下,这项统计量服从一个给定的概率分布,而这在另一种假设下则不然。从而若检验统计量的值落在上述分布的临界值之外,则可认为前述零假设未必正确。统计学中,用于检验假设量是否正确的量。常用的检验统计量有t统计量,Z统计量等。
6、实例
我们这里举2个例子:
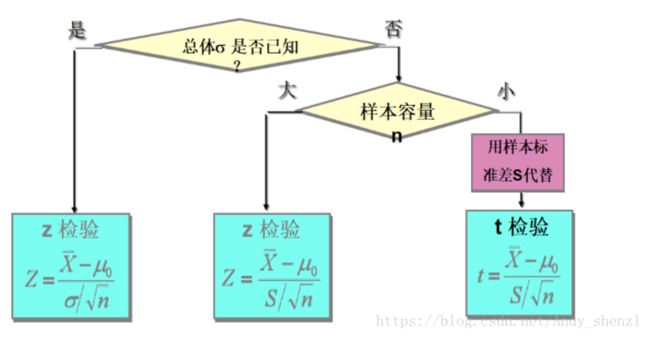
首先我们先引入一个检验统计量分布的选择规则
例1:
某机床厂加工一种零件,根据经验知道,该厂加工零件的椭圆度近似服从正态分布,其总体均值为μ=0.081mm,总体标准差为σ= 0.025 。今换一种新机床进行加工,抽取n=200个零件进行检验,得到的椭圆度为0.076mm。试问新机床加工零件的椭圆度的均值与以前有无显著差异?(α=0.05)
我们知道总体均值和总体方差,根据上图的规则可以看出我们可以用Z统计量:
例2:
以往通过大规模调查已知某地新生儿出生体重为3.30kg。从该地难产儿中随机抽取35名新生儿,平均出生体重为3.42kg,标准差为0.40kg,问该地难产儿出生体重是否与一般新生儿体重不同?
本例自由度v=n-1=35-1=34,查表得得t0.05/2,34=2.032。 因为t < t0.05/2,34,故P>0.05,按 α=0.05水准,不拒绝H0,差别无统计学意义,尚不能认为该地难产儿与一般新生儿平均出生体重不同。
以上就是对假设检验思想的一个简单介绍,其实对于理论的介绍理解起来比较晦涩,就像我们用1+1=2很简单,要是理解1+1为什么等于2就难了。假设检验在运用的时候就像最后的两个例子,其实是很简单的,但是对于理论的理解就需要比较长的时间。
欢迎关注微信公众号: