遗传算法学习笔记一之遗传算法工作原理
参考内容原址:https://www.analyticsvidhya.com/blog/2017/07/introduction-to-genetic-algorithm/
1,遗传算法理论的由来
我们先从查尔斯达尔文的一句名言开始:
能够生存下来的往往不是最强大的物种,也不是最聪明的物种,而是最能适应环境的物种。
2,生物学的启发
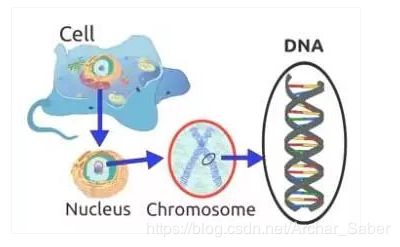
相信你还记得这句话:细胞是所有生物的基石。由此可知,在一个生物的任何一个细胞中,都有着相同的一套染色体。所谓染色体,就是指由DNA组成的聚合体。
传统上看,这些染色体可以被由数字0和1组成的字符串表达出来。
一条染色体有基因组成,这些基因其实就是组成DNA的基本结构,DNA上的每个基因都编码了一个独特的性状,比如头发或者眼睛的颜色。
3,遗传算法的定义
遗传算法实际上就是,尽力在某种程度上模拟进化的过程。
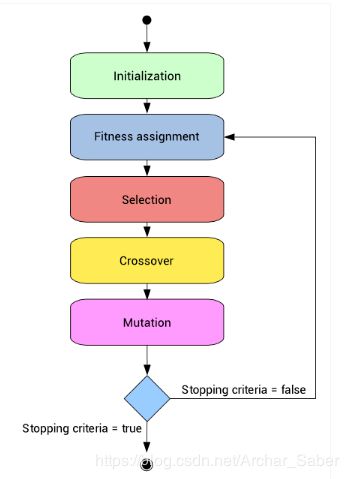
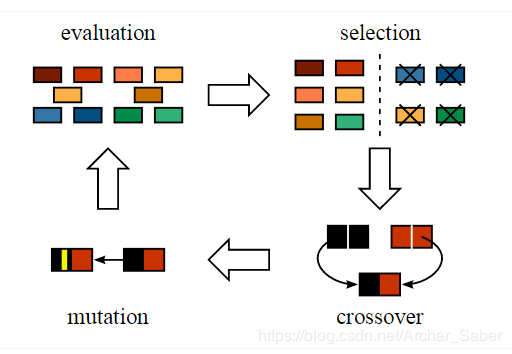
为了形式化定义一个遗传算法,我们可以将它看做一个优化方法,它可以尝试找出某些输入,凭借这些输入我们便可以得到最佳的输出值或者是结果。遗传算法的工作方式也源自于生物学,具体流程如下图:
那么现在我们来逐步理解下整个流程。
4,遗传算法具体步骤
为了让讲解更为简便,我们先来理解一下著名的组合优化问题【背包问题】。如果你还不太懂,这里有一个我的解释版本。
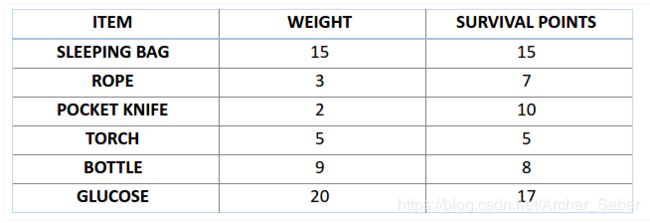
比如,你准备要去野游1个月,但是你只能背一个限重30公斤的背包。现在你有不同的必需物品,它们每一个都有自己的【生存点数】(具体在下表中已给出)。因此,你的目标是在有限的背包重量下,最大化你的【生存点数】。
4.1 初始化
这里我们用遗传算法来解决这个背包问题。第一步是定义我们的总体。总体中包含了个体,每个个体都有一套自己的染色体。
我们知道,染色体可表达为二进制数串,在这个问题中,1代表接下来位置的基因存在,0代表着丢失。
现在,我们将图中的4条染色体看做我们的总体初始值。
4.2 适应度函数
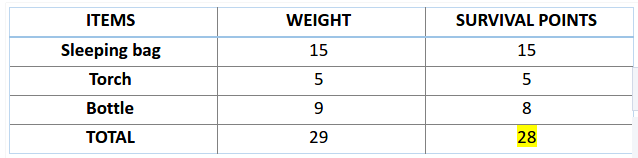
接下来,让我们来计算一下前两条染色体的适应度分数,对于A1染色体【100110】而言,有:
类似地,对于A2染色体【001110】来说,有:
对于这个问题,我们认为,当染色体包含更多生存分数时,也就意味着它的适应性更强。
因此,由图可知,染色体1适应性强于染色体2.
4.3 选择
现在,我们可以开始从总体中选择合适的染色体,来让他们互相交配,产生自己的下一代了。这个是进行选择操作的大致想法,但是这样将会导致染色体在几代后相互差异减小,失去了多样性。因此,我们一般会进行【轮盘赌选择法】。
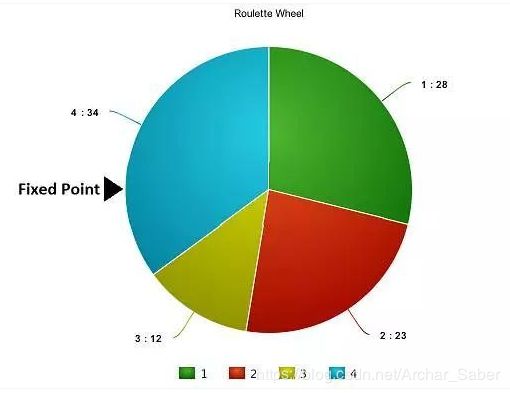
想象有一个轮盘,现在我们将它分割为m个部分,这里的m代表我们总体中染色体的个数。每条染色体在轮盘上占有的区域面积将根据适应度分数来成比例表示出来。
基于上图中的值,我们建立如下轮盘。
现在,这个轮盘开始旋转,我们将被图中固定的指针指到的那片区域选为第一个亲本。然后,对于第二个亲本,我们进行同样的操作。有时候我们也会在途中标注两个固定 指针,如下图:
通过这种方法,我们就可以在一轮中就获得两个亲本。我们将这种方法称为【随机普遍选择法】
4.4 交叉
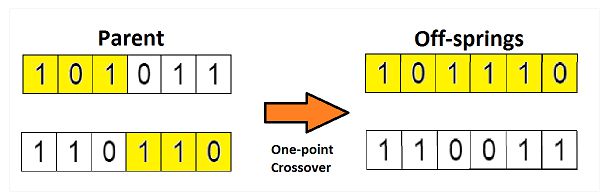
在上一个步骤中,我们已经选择出了可以产生后代的亲本染色体。那么用生物学的话说,所谓【交叉】,其实就是指的繁殖。我们现在来对染色体1和染色体4进行【交叉】,如下图:
这是交叉最基本的形式,我们称其为【单点交叉】。这里我们随机选择一个交叉点,然后,将交叉点前后的染色体部分进行染色体间的交叉对调,于是就产生了新的后代。
如果你设置两个交叉点,那么这种方法被称为【多点交叉】,如下图:
4.5 变异
在后代的生长过程中,它们体内的基因会发生一些变化,使得他们与父母不同。这个过程我们称为【变异】,它可以被定义为染色体上发生的随机变化,正是因为变异,种群中才会存在多样性。
下图为变异的一个简单实例:
变异完成之后,我们就得到了新个体,进化也就完成了,整个过程如下图:
在进行完一轮遗传变异之后,我们用适应度函数对这些新的后代进行验证,如果函数判定他们的适应度足够,那么就会用他们从总体中替代掉那些适应度不够的染色体。这里有个问题,我们最终应该以什么标准来判断后代达到了最佳适应度水平呢?
一般来说,有如下终止条件:
在进行x次迭代之后,总体没有什么太大改变。
我们事先为算法定义好了进化的次数。
当我们的适应度函数已经达到了预先定义的值。