np.mgrid(),np.meshgrid()与三维画图

import numpy as np

X = np.mgrid[-5:5:5]

X1 = np.mgrid[-5:5:5j]

Y1,Y2 = np.mgrid[-5:5,10:17]

Z1,Z2,Z3 = np.mgrid[-5:5,10:17,1:3]

print(X)
print(X1)
print(Y1,Y2)

输出：

[-5  0]
[-5.  -2.5  0.   2.5  5. ]
(array([[-5, -5, -5, -5, -5, -5, -5],
       [-4, -4, -4, -4, -4, -4, -4],
       [-3, -3, -3, -3, -3, -3, -3],
       [-2, -2, -2, -2, -2, -2, -2],
       [-1, -1, -1, -1, -1, -1, -1],
       [ 0,  0,  0,  0,  0,  0,  0],
       [ 1,  1,  1,  1,  1,  1,  1],
       [ 2,  2,  2,  2,  2,  2,  2],
       [ 3,  3,  3,  3,  3,  3,  3],
       [ 4,  4,  4,  4,  4,  4,  4]]), array([[10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16],
       [10, 11, 12, 13, 14, 15, 16]]))

Meshgrid

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

x = np.arange(-5, 5, 0.1)
y = np.arange(-5, 5, 0.1)
xx, yy = np.meshgrid(x, y)
z = np.sin(xx**2 + yy**2) / (xx**2 + yy**2)

print(xx)
print(yy)

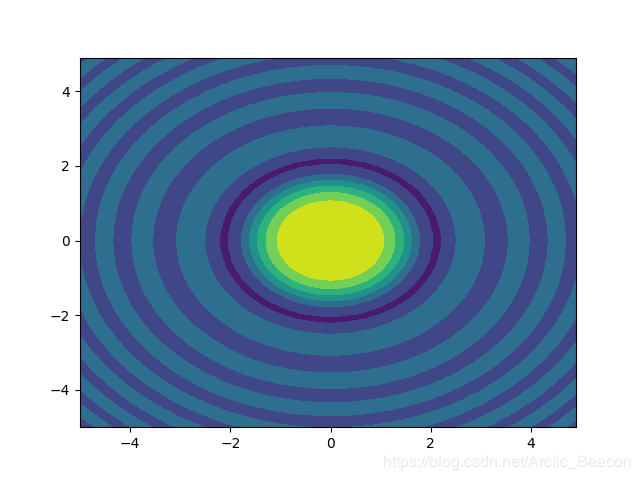
h = plt.contourf(x,y,z)

fig = plt.figure()
ax = Axes3D(fig)
plt.xlabel(r'x',fontsize=20,color='cyan')
plt.ylabel(r'y',fontsize=20,color='cyan')
ax.plot_surface(xx, yy, z, rstride=1, cstride=1, cmap=cm.viridis)

plt.show()

输出

[[-5.  -4.9 -4.8 ...,  4.7  4.8  4.9]
 [-5.  -4.9 -4.8 ...,  4.7  4.8  4.9]
 [-5.  -4.9 -4.8 ...,  4.7  4.8  4.9]
 ...,
 [-5.  -4.9 -4.8 ...,  4.7  4.8  4.9]
 [-5.  -4.9 -4.8 ...,  4.7  4.8  4.9]
 [-5.  -4.9 -4.8 ...,  4.7  4.8  4.9]]
[[-5.  -5.  -5.  ..., -5.  -5.  -5. ]
 [-4.9 -4.9 -4.9 ..., -4.9 -4.9 -4.9]
 [-4.8 -4.8 -4.8 ..., -4.8 -4.8 -4.8]
 ...,
 [ 4.7  4.7  4.7 ...,  4.7  4.7  4.7]
 [ 4.8  4.8  4.8 ...,  4.8  4.8  4.8]
 [ 4.9  4.9  4.9 ...,  4.9  4.9  4.9]]

 

 

这类函数的核心思想是遍历每一个坐标网格，每一个坐标网格都有一个坐标（二维向量）与其对应。3D情况当然是每个坐标是一个三维向量。x坐标gridding当然是x方向渐变，y方向不变；y坐标gridding当然是y方向渐变，x方向不变。