笔记(总结)-XGBoost的前世今生
现今的各类数据挖掘比赛中,决策树模型占据了半壁江山(另外半壁基本就是神经网络模型)。决策树,本质上来说就是通过一系列的“规则”将样本集不断划分归类,最后归为同一类的样本被认为是相似的,赋予相同的预测值。
决策树相对于其他机器学习模型来说:
- 可解释较强(规则划分)
- 能够有合理的调参依据(树深度、叶子节点个数等参数概念都很直观)
- 适用于bagging和boosting方式的建模(Random Forest、Adaboost、GBDT等)
- 有高效的并行化实现(XGBoost、LightGBM等)
…
本文主要围绕XGBoost进行阐述,在网上查阅过很多博客,各有亮点,但总是看完之后还带有一些疑问。阅读了原作者的论文和讲解PPT后,总结相关概念,将思路过程记录下来。
拆解XGBoost概念如下
什么是XGBoost?
XGBoost是华盛顿大学陈天奇开发的开源工具包,是GBDT的高效实现,同时加入了适当改进。
什么是GBDT?
GBDT(Gradient Boosting Decision Tree)。GBDT有很多简称,有GBT(Gradient Boosting Tree), GTB(Gradient Tree Boosting ), GBRT(Gradient Boosting Regression Tree), MART(Multiple Additive Regression Tree),其实都是指的同一种算法。
什么是Boosting?
Boosting是一类将弱学习器提升为强学习器的算法框架。从初始样本中训练出一基学习器,根据训练结果对训练过程做出调整,调整过后再重新训练另一学习器,不断重复这个过程,最终把所有学习器的预测结果加权结合。
什么是Decision Tree?
Decision Tree(决策树)是一类通过规则将样本集不断进行划分的算法。初始时,所有样本都属于根节点。根据规则,将样本分为两拨,分别划分到根节点下属的两个节点中,重复这个过程直到划分结束。最后可能得到一棵不规则的二(多)叉树。叶子节点中的样本被认为是相似的,将根据某一依据赋予相同的预测值。
由最底层概念Decision Tree开始,逐步改善得到XGBoost
决策树做分类
以二分类问题(人是否喜欢上网)为例。根节点时,选择能描述样本集(不同的人)的某一属性(年龄),不同样本具有不同的属性值,根据某一属性值(25岁)能将样本分成两拨(25岁以上或以下)。重复这个过程,直到产生所有叶子节点(满足节点分裂停止条件,如树的深度达到最大限制等)。每个叶子节点中有很多样本,利用投票机制来决定该节点是不是喜欢上网的人群(共18人,12人喜欢,6人不喜欢,则该节点为喜欢上网人群)。对于未知的人,将其按特征不断划分,最终落到叶子节点中,根据该节点之前的标记来预测该人是否喜欢上网。
在分裂节点时,如何选择合适的属性和划分的属性值呢?我们希望分裂过后,能将上网的人和不上网的人尽量区分开。例如,规则A将20人(10人喜欢上网、10人不喜欢)分为S1 10人、S2 10人两拨。S1中5个人喜欢上网,5人不喜欢,S2也是如此。那么这样对“是否喜欢上网”这一问题的解决毫无帮助。为了衡量这个标准,可以利用Gini系数和熵来衡量,在此不做展开。
决策树做回归
回归问题的待预测值是连续的,最终划分到每个叶子节点中的样本可能具有完全不同的标签(如15岁、20岁、25岁),此时不再满足投票机制。改为取所有样本标签的平均值作为该节点的预测值(20岁)。在节点划分时,Gini系数和熵也无法衡量连续情况下划分的好坏,改为使用均方误差(样本标签平均值作为预测)的方式,使得分裂后节点的均方误差最小。
Boosting Decision Tree
考虑每轮决策树来拟合样本残差(残差=真实值-预测值)。假设预测年龄的回归问题,某样本为30岁,第一轮预测值为24岁。如果是AdaBoost,则会调整该样本权重,在下一轮中着重预测该样本,最后将树的预测结果加权求和。我们不这么做,将下一轮该样本的预测目标改为30-24=6岁,即下一轮样本标签发生了变化,不再是原有标签,而是残差。若下一轮预测值为4岁,则再下一轮预测目标改为30-(24+4)=2岁。当待预测目标不断减小接近0时,我们就可以近乎完美地预测该样本,预测值=24+4+…近似等于预测目标。
Gradient Boosting Decision Tree
结合机器学习中常用的梯度下降的思想重新来看这个问题。给定特定的优化目标函数L,我们想要针对变量α进行优化,求得L关于α的梯度即可更新α。在Boosting Decision Tree中,目标函数其实就是衡量预测值和真实标签的损失函数,我们实际上是想要对预测值进行不断优化,达到减小损失函数的目的。这样看来可以运用梯度下降的思想。当Boosting Decision Tree中使用平方误差作为样本损失L时,对于预测值f(x)求梯度得到的正是残差(如下图所示),此时将残差作为下一颗树的标签,相当于对L关于f(x)的梯度进行拟合,最终将不同树的结果求和,则相当于进行了变相的梯度下降!上述f(x)可以看做之前轮数预测结果的求和(24+4=28岁),是关于样本x的预测函数,因此GBDT也可以看做函数空间的梯度下降。
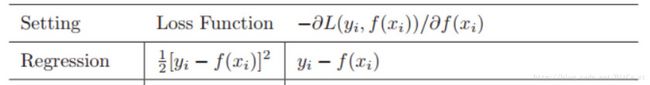
此时我们得到了GBDT的核心思想:用损失函数关于之前轮预测值的负梯度来近似本轮损失。利用负梯度作为标签来拟合本轮的决策树。算法如下:
- 初始化预测函数
- M轮建树过程,每轮对于每个样本求损失函数关于之前预测值f(x)的负梯度,作为本轮决策树的拟合目标
- 求得本轮决策树的叶子节点的待预测值γ,使得f(x)+γ的新预测值能最小化损失函数
- 更新预测值f(x)=f(x)+γ
可以看到,目标函数是对预测函数求导,即函数空间的梯度下降。
XGBoost
XGBoost是GBDT的高效并行实现,还加入了一些算法上的改进。这个改变过程不是一蹴而就的,原作者也是借鉴了前人的很多思想。本人水平有限,就不再叙述这个演进过程,而是直接结合原作者的slides直接给出XGBoost的逻辑框架。
对于机器学习问题,我们一般会分析样本集的分布特点,总结其与待预测值之间的关系,构造一个目标函数。通过优化目标函数从而达到逐步构建模型的目的。通常目标函数结构如下:

其中Training Loss也叫“经验风险”(empirical risk),用于描述模型与数据的契合程度。Regularization为“正则化项”,也称为“结构风险”(structural risk),用于描述模型的复杂度。我们想最小化该目标函数,既想模型能较好地拟合训练数据,在训练集上偏差(bias)较小,又想得到一个复杂度低的模型。
对于GBDT,我们可以看到,算法中的目标函数只有Training Loss。考虑补充正则化项,假设GBDT由k棵树构成,得到XGBoost的目标函数如下:
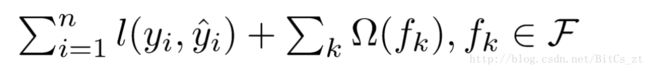
前一项衡量模型在n个样本点上的训练误差,后一项衡量所有树的模型复杂度。再结合boosting将预测函数写开,可以得到第t轮和前一轮迭代关系:

在第t轮中,我们需要确定的是f函数,f和前t-1轮预测函数求和后能最小化目标函数:
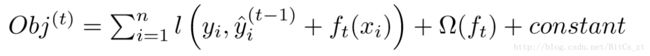
结合GBDT的算法,在第t轮中,我们是用目标函数(损失函数)对预测函数的负梯度,作为样本标签来拟合本轮的决策树。XGBoost中使用一阶偏导(即梯度)和二阶偏导来拟合,原论文没有提及这么做的原因,不过根据泰勒公式:

二阶展开比一阶展开具有更好的逼近效果。上式中的 x x 相当于 ŷ (t−1) y ^ ( t − 1 ) ,而 Δ Δ x x 则相当于 ft(xi) f t ( x i ) ,由此将第t轮的目标函数转化为:
![]()
其中 gi g i 和 hi h i 分别为一阶、二阶导数:
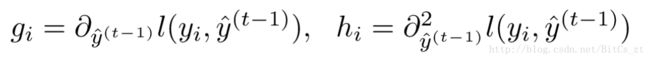
只保留目标函数中跟第t轮有关的项,去除常数项和前t-1轮的预测误差,目标函数变为:
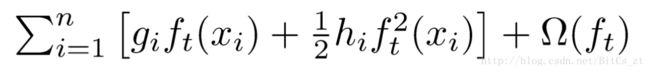
对于决策树来说, ft(xi) f t ( x i ) 实际上是一个简单的映射函数,对每个样本给出预测值,决策树中就是叶子节点最后的预测值:
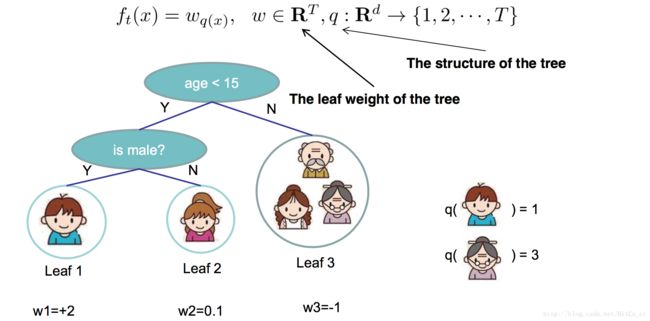
上式中, w w 是每个叶子节点的估计值, q q 是一个简单的对应关系,把每个样本映射到对应的叶子节点。上图是对 ft(xi) f t ( x i ) 的一个形象说明。
对于目标函数中的模型复杂度,不使用常见的 L2、L1 L 2 、 L 1 正则项,针对决策树的特殊结构定义模型复杂度如下:
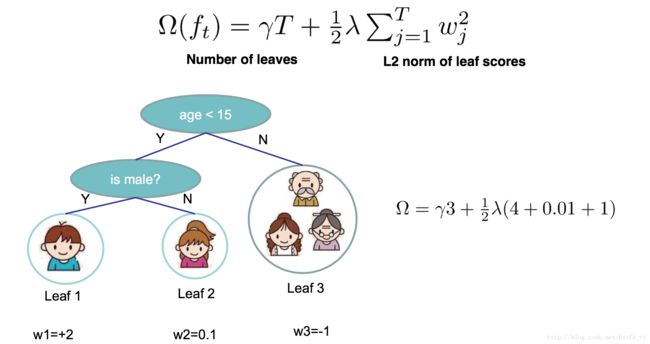
T T 是叶子节点个数, wj w j 是每个叶子节点的预测值。
到目前为止,目标函数是以样本为单位进行组织,将其转化为以叶子节点进行组织:

其中 Ij I j 是第 j j 个叶子节点中包含的所有样本的下标集合。可以看到上式实际上是 T T 个关于 w w 的二次函数和。对二次函数求解最优有:
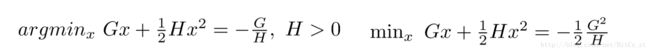
转换目标函数表示方式:

其中:

由此,当给定我们树的结构( q(x) q ( x ) 即每个样本属于哪个叶子节点),每个叶子节点的预测值可以通过解上述二次函数得到:
可以看到,XGBoost将目标函数进行二阶泰勒展开并进行一系列的变换,最终表示成了关于叶子节点预测值的二次函数。而求解这个二次函数所使用到的参数则是我们在最初计算的一阶偏导、二阶偏导。传统的GBDT,是先计算出一阶偏导作为标签,然后用决策树来进行拟合,叶子节点预测值是由最终叶子节点中所有节点的标签平均得到的。XGBoost将待预测值作为目标函数的变量进行优化求解,更为直接。
下面我们来具体分析构建一棵树的过程。由上可得,给定一棵树的结构,可以求得最优叶子节点预测值和目标函数最小值。枚举树的结构是不现实的,每一步分裂节点时可以考虑各类特征、每个特征的分裂点等,导致树的结构几乎是无穷多。一般来说,是采用贪心的做法。在当前节点,选取增益最大的方式进行分裂。虽然这样可能无法达到全局最优,但是也算是有限算力下的最好办法了。贪心分裂在原作者slides里说的很清楚:

分裂增益实际上就是分裂前后目标函数的差值,可以看到在最后还减去了衡量叶子节点个数复杂度的参数γ,此处表示多引入一个叶子节点所增加的模型复杂度的开销(原来的一个叶子节点分裂变成左右两个叶子节点),这种做法实际上是限制了节点的分裂,减少了过拟合的可能性。
对于待分裂节点,遍历每个属性。针对每个属性,将样本按属性值大小排序。任意属性值都能将样本划分为两部分,扫描一遍样本,计算每个划分点的 GL和GR G L 和 G R ,即可找到最佳分裂点。在XGBoost中,还采取了类似Random Forest中列采样(column subsampling)的方式,不遍历每个属性,而是从中随机抽取一部分进行计算,最终选择增益最大的属性。
总结算法,对于每一轮迭代:
- 计算所有样本的一阶偏导、二阶偏导。
- 对于待分裂节点,贪心地选择最佳分裂点。
- 达到分裂停止条件时停止分离。
- 将本轮得到的预测函数添加到之前轮数的预测函数上。
其中第4步中,通常采取以下改进方式:
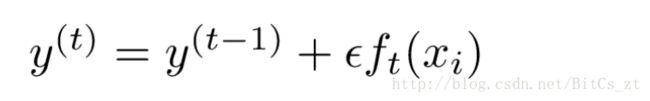
其中 ϵ ϵ 表示步长(step-size or shrinkage),这表示我们只将本轮得到的结果的一部分加到预测函数中,减少了过拟合,同时更多地保留在后面轮数中发掘信息的可能性。
至此XGBoost的算法部分基本讲完了。可以看到,从最初的决策树到最后的XGBoost,改变是巨大的,同时很多改变都有着来自其他算法精华的指导思想作为支撑。相比于GBDT,XGBoost在算法上没有巨大改变(相比于决策树和Boosting结合,GBDT使用函数负梯度拟合来说),但其在工程上的高效并行实现,使得该算法能真正成为“老少咸宜”的工具,广泛使用于各类场景。在海量数据下,快速高效的算法能压缩迭代周期,使得调试的代价变低,极大地提高生产效率,而XGBoost不仅达到了速度上的巨大飞跃,也在算法上做了诸多改善,真正做到了精准、高效。
参考链接之前的笔记总结了:
笔记-GBDT&Xgboost
同时还参考了原作者陈天奇的论文和slides,有条件的话还是建议大家能阅读原论文,对于XGBoost的理解最为直观。