Keras深度学习试验（二）：卷积网络CNN

本文通过试验对比分析卷积神经网络（CNN）主要参数和算法的效果。工具：Keras，数据集：mnist。 参考《Keras深度学习实战》一书。
（1）baseline(LeNet):首次运行代码会自动加载mnist

import numpy as np
from keras import backend as K
from keras.models import Sequential
from keras.layers.convolutional import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.layers.core import Dense, Activation
from keras.layers.core import Flatten
from keras.datasets import mnist
from keras.utils import np_utils
from keras.optimizers import Adam
import matplotlib.pyplot as plt
np.random.seed(0)

NB_EPOCH = 20
BATCH_SIZE=128
VERBOSE=1
OPTIMIZER=Adam()
VALIDATION_SPLIT=0.2
IMG_ROWS, IMG_COLS = 28, 28
NB_CLASSES = 10
INPUT_SHAPE = (1, IMG_ROWS, IMG_COLS)

(X_train, y_train), (X_test, y_test)= mnist.load_data()
K.set_image_dim_ordering('th')#维度排列顺序，在Conv2D中默认按照'th',所以需要先转为'th'
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train = X_train/255
X_test = X_test/255

X_train = X_train[:, np.newaxis, :, :]#插入新的轴，使维度由(60000,28,28)变为(60000,1,28,28)
X_test = X_test[:, np.newaxis, :, :]
print (X_train.shape[0],'train samples')
print (X_test.shape[0],'test samples')

Y_train = np_utils.to_categorical(y_train,NB_CLASSES)
Y_test = np_utils.to_categorical(y_test,NB_CLASSES)
##LeNet:
model = Sequential()
#Conv2D(卷积核数目，卷积核尺寸，补0策略（same表示保留边界卷积结果，可使输入输出shape相同）)
model.add(Conv2D(20, kernel_size=5,padding='same', input_shape=INPUT_SHAPE))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2),strides=(2,2)))
model.add(Conv2D(50,kernel_size=5, border_mode='same'))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2),strides=(2,2)))
model.add(Flatten())
model.add(Dense(500))
model.add(Activation('relu'))
model.add(Dense(NB_CLASSES))
model.add(Activation('softmax'))

model.compile(loss='categorical_crossentropy',optimizer=OPTIMIZER,metrics=['accuracy'])
history = model.fit(X_train, Y_train, batch_size=BATCH_SIZE, epochs=NB_EPOCH,verbose=VERBOSE,
                    validation_split=VALIDATION_SPLIT)
score=model.evaluate(X_test, Y_test, verbose=VERBOSE)
print('Test score:', score[0])
print('Test accuracy:',score[1])
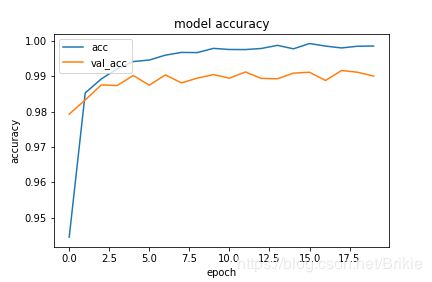
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['acc','val_acc'],loc='upper left')
plt.show()

在8核2.5G CPU上单个epoch运行时间约108s，在Tesla P4 GPU上单个epoch运行时间约5s。运行结果为：

Epoch 20/20
48000/48000 [==============================] - 5s 97us/step - loss: 0.0040 - acc: 0.9986 - val_loss: 0.0519 - val_acc: 0.9897
10000/10000 [==============================] - 1s 91us/step
Test score: 0.04197419135123564
Test accuracy: 0.9905

（2）池化层的作用

池化层	2×2+2×2	不要	2×2+0	3×3+3×3
Test acc	0.9905	0.9904	0.9918	0.9890
速度/epoch	5s	15s	6s	3s

可见，池化层主要是用来提高运算速度的，如果不使用池化层，精度也没有很大变化，但运算速度慢很多。池化通常使用2×2，大尺寸会降低预测精度。
（3）卷积核的尺寸

卷积核尺寸	5	4	3	2	1	6	8	10
Test acc	0.9905	0.9918	0.9902	0.9898	0.9472	0.9926	0.9909	0.9912

本例中，卷积核尺寸在3~10之间似乎没有太大影响。卷积核为1时等于没有用卷积，所以预测精度和全连接网络差不多。
（4）改变卷积核数目
上面的LeNet中使用了两个卷积层，分别有20和50个卷积核。下面试验改变两个卷积层的数量，看效果。

卷积层	20+50	50+20	20+20	20+100	50+50	100+100
Test acc	0.9905	0.9868	0.9899	0.9886	0.9918	0.9923

卷积核数量增加后，相当于提炼了更多的特征，预测精度会有所提高，当然预算速度也会变慢。
（5）增加卷积层

卷积层	20	20+50	20+30+50	20+30+40+50
Test acc	0.9875	0.9905	0.9930	0.9906
时间 /epoch	4s	5s	4s	4s

增加深度后似乎并没有增加精度，当然使用20+30+50的结构取得了不错的成绩，但我感觉这是运气成分。增加深度后运算速度却没有变慢，这个有可能是对GPU的利用率提高了。
（6）全连接层的作用
baseline中使用了500个节点的全连接层用来展平卷积层提取的特征，下面改变全连接层的节点数，发现只要节点不特别的少，则对结果没有什么影响:

全连接层节点数	500	100	200	1000	10
Test acc	0.9905	0.9912	0.9903	0.9914	0.9875

（7）Dropout层的作用
在baseline中给两个卷积层和全连接层加上dropout层，0表示不使用dropout，发现dropout有明显作用。

Dropout设置	0+0+0.5	0+0.25+0.5	0.25+0.25+0.5	0.5+0.5+0.5
Test acc	0.9924	0.9925	0.9935	0.9940