[译]为任意网格计算tangent空间的基向量
[译]为任意网格计算tangent空间的基向量
Computing Tangent Space Basis Vectors for an Arbitrary Mesh (Lengyel’s Method)
Modern bump mapping (also known as normal mapping) requires that tangent plane basis vectors be calculated for each vertex in a mesh. This article presents the theory behind the computation of per-vertex tangent spaces for an arbitrary triangle mesh and provides source code that implements the proper mathematics.
现代凹凸映射(也被称为法线映射)要求为网格中的每个顶点计算出其tangent平面基向量。本文描述了对任意三角形网格计算逐顶点tangent空间的数学理论,还提供了实现数学计算的源代码。
Mathematical Derivation 数学推导
[This derivation also appears in Mathematics for 3D Game Programming and Computer Graphics, 3rd ed., Section 7.8.]
[这一推导也出现在Mathematics for 3D Game Programming and Computer Graphics, 3rd ed.,章节7.8。]
We want our tangent space to be aligned such that the x axis corresponds to the u direction in the bump map and the y axis corresponds to the v direction in the bump map. That is, if Q represents a point inside the triangle, we would like to be able to write
我们想让我们的tangent空间这样布局:其x轴对应凹凸贴图的u方向,y轴对应凹凸贴图的v方向。(译者注:这话的意思是,想象一下,将正方形贴图拿起来,将其(0, 0)位置固定到顶点上,此时,其u方向就是我们要找的tangent空间的x轴,其v方向就是我们要找的tangent空间的y轴,三角形面的法线方向就是我们要找的tangent空间的z轴。显然,这样的x轴y轴对,有无数个,我们需要的,是其中唯一的一个。是哪个呢?继续看原文。。。)换句话说,设Q代表三角形内部的一个点,我们希望有
where P0 is the position of one of the vertices of the triangle, and (u0, v0) are the texture coordinates at that vertex. The vectors T and B are the tangent and bitangent vectors aligned to the texture map, and these are what we’d like to calculate.
其中P0是三角形的某个顶点,(u0, v0)是此顶点的纹理坐标。向量T和B分别是tangent 和bitangent 向量,它们分别与纹理贴图的轴平行,是我们想求得的未知数。(译者注:这个公式的意思是,当Q位于P0P1的中点时,u就位于u0u1的中点,等等,当Q位于P0P1P2内部的某点时,通过缩放纹理,会让(u, v)位于同贴图上同样的位置上。顶点P0P1P2的位置构成的三角形A,与顶点P0P1P2的纹理坐标构成的三角形B,两者上的点,即Q和(u, v),建立了一个线性的对应关系。能够使这2个三角形A和B的这样线性关系成立的那个T和B,就是我们需要的唯一的结果。)
Suppose that we have a triangle whose vertex positions are given by the points P0, P1, and P2, and whose corresponding texture coordinates are given by (u0, v0), (u1, v1), and (u2, v2). Our calculations can be made much simpler by working relative to the vertex P0, so we let
假设我们有一个三角形,其顶点位置由P0、P1和P2给定,其对应的纹理坐标由(u0, v0)、(u1, v1)和(u2, v2)给定。通过相对于P0(进行归零),我们的计算可以简化很多,所以我们让
and
且
(译者注:这其实就是让P0和(u0, v0)归零,将三角形A和B都放到原点上。由于A和B是线性关系,所以这样的平移不会影响其线性关系。)
We need to solve the following equations for T and B.
我们需要求解下述等式中的T和B。
This is a linear system with six unknowns (three for each T and B) and six equations (the x, y, and z components of the two vector equations). We can write this in matrix form as follows.
这是个线性系统,有6个未知数(T和B各3个)和6个等式(2个向量等式的x、y和z分量)。我们可以将它改写为下述矩阵形式。
Multiplying both sides by the inverse of the (s, t) matrix, we have
两边同时乘以(s, t)矩阵的逆矩阵(译者注:然后将等号左右互换位置),我们有
This gives us the (unnormalized) T and B vectors for the triangle whose vertices are P0, P1, and P2. To find the tangent vectors for a single vertex, we average the tangents for all triangles sharing that vertex in a manner similar to the way in which vertex normals are commonly calculated. In the case that neighboring triangles have discontinuous texture mapping, vertices along the border are generally already duplicated since they have different mapping coordinates anyway. We do not average tangents from such triangles because the result would not accurately represent the orientation of the bump map for either triangle.
这给出了顶点为P0、P1和P2的三角形的(译者注:即face的)(未标准化的)T和B向量。为了找到顶点的tangent向量,我们对所有共享此顶点的三角形的tangent取平均值,类似于计算顶点的法线那样的方式。当相邻的三角形的纹理映射不连续时,其共享边上的顶点一般都已经被复制了一份,因为它们的纹理坐标毕竟是不同的。(译者注:想象一个人头部模型的三维网格及其贴图,贴图上的后脑勺部分肯定是被分开的,鼻子部分肯定是挨着的,所以网格上描述后脑勺的顶点是被复制了一份,是可以“掰开”的。还是不能想象的话,上网找找模型及其贴图,或者看看电影《画皮》。)我们不把这样的三角形计入平均化过程,因为其结果无法准确地代表(两个三角形中任意一个三角形的)凹凸贴图的朝向。(译者注:由于后脑勺的顶点被复制了一份,就不再共享边了,所以也不会计入平均化过程。)
Once we have the normal vector N and the tangent vectors T and B for a vertex, we can transform from tangent space into object space using the matrix
一旦我们有了顶点的法线向量N和tangent向量T和B,我们就可以实施从tangent空间到object空间的转换了(用矩阵的形式)
To transform in the opposite direction (from object space to tangent space—what we want to do to the light direction), we can simply use the inverse of this matrix. It is not necessarily true that the tangent vectors are perpendicular to each other or to the normal vector, so the inverse of this matrix is not generally equal to its transpose. It is safe to assume, however, that the three vectors will at least be close to orthogonal, so using the Gram-Schmidt algorithm to orthogonalize them should not cause any unacceptable distortions. Using this process, new (still unnormalized) tangent vectors T′ and B′ are given by
为了向反方向变换(从object空间到tangent空间——我们想对光照方向这样做),我们直接使用此矩阵的逆矩阵即可。2个tangent向量未必是互相垂直的,它们也未必与法线向量垂直,所以此矩阵的逆矩阵未必等于其转置矩阵。(译者注:这是个数学定理吧,由3个互相垂直的向量构成的矩阵,其逆矩阵等于其转置矩阵。书到用时方恨少,有空学时最贪玩。)但可以安全地假设,这3个向量是接近互相垂直的,所以使用Gram-Schmidt算法来正交化它们,应该不会引起任何不可接受的失真。使用这个方法,新的(仍旧是未标准化的)tangent向量T′和B′由下述公式给出
Normalizing these vectors and storing them as the tangent and bitangent for a vertex lets us use the matrix
标准化这些向量,将其保存为顶点的tangent和bitangent,这样我们就可以使用矩阵
to transform the direction to light from object space into tangent space. Taking the dot product of the transformed light direction with a sample from the bump map then produces the correct Lambertian diffuse lighting value.
来将光线方向从object空间变换到tangent空间。对(变换后的光照方向)和(来自凹凸贴图的采样值)使用点积,就会产生正确的Lambertian漫反射光照值。
It is not necessary to store an extra array containing the per-vertex bitangent since the cross product N × T′ can be used to obtain mB′, where m = ±1 represents the handedness of the tangent space. The handedness value must be stored per-vertex since the bitangent B′ obtained from N × T′ may point in the wrong direction. The value of m is equal to the determinant of the matrix in Equation (*). You might find it convenient to store the per-vertex tangent vector T′ as a four-dimensional entity whose w coordinate holds the value of m. Then the bitangent B′ can be computed using the formula
没有必要用一个数组来保存逐顶点的bitangent,因为叉积N × T′可以用来获取mB′,其中m = ±1,表示tangent空间的惯用手(译者注:左手系or右手系)。惯用手值必须逐顶点地保存,因为用N × T′得到的bitangent B′可能指向错误的(译者注:即相反的)方向。m的值等于等式(*)中的矩阵的行列式(译者注:行列式其实就是一个数值)。你可能发现了,用四维向量保存逐顶点的tangent向量T′,其w分量保存m,比较方便。这样,bitangent B′就可以用下述公式计算
where the cross product ignores the w coordinate. This works nicely for vertex shaders by avoiding the need to specify an additional array containing the per-vertex m values.
其中的叉积忽略了w分量。这样就可以在顶点着色器中,避免指定一个额外的用于保存逐顶点的m值的数组,棒棒哒。
Bitangent versus Binormal 副切线 versus 副法线
The term binormal is commonly used as the name of the second tangent direction (that is perpendicular to the surface normal and u-aligned tangent direction). This is a misnomer. The term binormal pops up in the study of curves and completes what is known as a Frenet frame about a particular point on a curve. Curves have a single tangent direction and two orthogonal normal directions, hence the terms normal and binormal. When discussing a coordinate frame at a point on a surface, there is one normal direction and two tangent directions, which should be called the tangent and bitangent.
名词binormal 通常用作第二个切线方向的名字(即垂直于表面法线和u方向的切线)。这是个误称。名词binormal出现在对曲线(curves )的研究中,它是Frenet坐标系的一部分,用于描述曲线上的点。曲线有一个切线方向和2个垂直的法线方向,因此有了名词normal和binormal。当讨论一个表面(surface)上一点处的坐标系时,有1个法线和2个切线方向,所以应当被称为tangent和bitangent。
Source Code 源代码
The code below generates a four-component tangent T in which the handedness of the local coordinate system is stored as ±1 in the w-coordinate. The bitangent vector B is then given by B = (N × T) · Tw.
下述代码计算了四维tangent T,其tangent坐标系的惯用手(其值为±1)保存在w分量。之后,bitangent向量B可以通过B = (N × T) · Tw给出。
1 #include "Vector4D.h" 2 3 4 struct Triangle 5 { 6 unsigned short index[3]; 7 }; 8 9 10 void CalculateTangentArray(long vertexCount, const Point3D *vertex, const Vector3D *normal, 11 const Point2D *texcoord, long triangleCount, const Triangle *triangle, Vector4D *tangent) 12 { 13 Vector3D *tan1 = new Vector3D[vertexCount * 2]; 14 Vector3D *tan2 = tan1 + vertexCount; 15 ZeroMemory(tan1, vertexCount * sizeof(Vector3D) * 2); 16 17 for (long a = 0; a < triangleCount; a++) 18 { 19 long i1 = triangle->index[0]; 20 long i2 = triangle->index[1]; 21 long i3 = triangle->index[2]; 22 23 const Point3D& v1 = vertex[i1]; 24 const Point3D& v2 = vertex[i2]; 25 const Point3D& v3 = vertex[i3]; 26 27 const Point2D& w1 = texcoord[i1]; 28 const Point2D& w2 = texcoord[i2]; 29 const Point2D& w3 = texcoord[i3]; 30 31 float x1 = v2.x - v1.x; 32 float x2 = v3.x - v1.x; 33 float y1 = v2.y - v1.y; 34 float y2 = v3.y - v1.y; 35 float z1 = v2.z - v1.z; 36 float z2 = v3.z - v1.z; 37 38 float s1 = w2.x - w1.x; 39 float s2 = w3.x - w1.x; 40 float t1 = w2.y - w1.y; 41 float t2 = w3.y - w1.y; 42 43 float r = 1.0F / (s1 * t2 - s2 * t1); 44 Vector3D sdir((t2 * x1 - t1 * x2) * r, (t2 * y1 - t1 * y2) * r, 45 (t2 * z1 - t1 * z2) * r); 46 Vector3D tdir((s1 * x2 - s2 * x1) * r, (s1 * y2 - s2 * y1) * r, 47 (s1 * z2 - s2 * z1) * r); 48 49 tan1[i1] += sdir; 50 tan1[i2] += sdir; 51 tan1[i3] += sdir; 52 53 tan2[i1] += tdir; 54 tan2[i2] += tdir; 55 tan2[i3] += tdir; 56 57 triangle++; 58 } 59 60 for (long a = 0; a < vertexCount; a++) 61 { 62 const Vector3D& n = normal[a]; 63 const Vector3D& t = tan1[a]; 64 65 // Gram-Schmidt orthogonalize 66 tangent[a] = (t - n * Dot(n, t)).Normalize(); 67 68 // Calculate handedness 69 tangent[a].w = (Dot(Cross(n, t), tan2[a]) < 0.0F) ? -1.0F : 1.0F; 70 } 71 72 delete[] tan1; 73 }
How to cite this article 如何引用本文
Lengyel, Eric. “Computing Tangent Space Basis Vectors for an Arbitrary Mesh”. Terathon Software, 2001. http://terathon.com/code/tangent.html
Copyright © 2001–2017, Terathon Software LLC
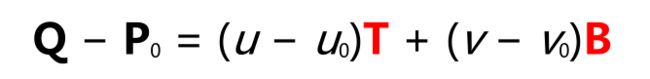
![[译]为任意网格计算tangent空间的基向量_第1张图片](http://img.e-com-net.com/image/info8/a2f9066f154a492da40e4da0bf040f8a.jpg)
![[译]为任意网格计算tangent空间的基向量_第2张图片](http://img.e-com-net.com/image/info8/13c1cd1834fe44bf85dff7abd9ae1cf1.jpg)
![[译]为任意网格计算tangent空间的基向量_第3张图片](http://img.e-com-net.com/image/info8/881c7808ff5c447984f3c522c8457fdd.jpg)
![[译]为任意网格计算tangent空间的基向量_第4张图片](http://img.e-com-net.com/image/info8/87be3facc5f74552aa841a56d0594be7.jpg)
![[译]为任意网格计算tangent空间的基向量_第5张图片](http://img.e-com-net.com/image/info8/00b748b1bbff48bdb7bfbb75e771d219.jpg)
![[译]为任意网格计算tangent空间的基向量_第6张图片](http://img.e-com-net.com/image/info8/f3d49a8b9e6146608f7949561a30aaad.jpg)
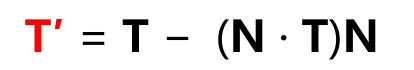

![[译]为任意网格计算tangent空间的基向量_第7张图片](http://img.e-com-net.com/image/info8/6a2de586e63c47e2ae3aa261d5d6e6b9.jpg)
