算法课堂实验报告（二）——python递归和分治（第k小的数，大数乘法问题）

python实现递归和分治

---

一、开发环境

开发工具：jupyter notebook 并使用vscode，cmd命令行工具协助编程测试算法,并使用codeblocks辅助编写C++程序
编程语言：python3.6

二、实验目标

1. 熟悉递归和分治算法实现的基本方法和步骤；

2. 学会分治算法的实现方法和分析方法：

三、实验内容

问题1，线性时间选择问题：
1） 在 4 59 7 23 61 55 46中找出最大值，第二大值，和第四大的值（要求不允许采用排序算法），并与第一章实现的快速排序算法进行比较。

2） 随机生成10000个数，要求找出其中第4999小的数，并与第一章实现的快速排序算法进行比较。

将4 59 7 23 61 55 46作为列表输入函数中，并且返回输出的结果

方法：直接遍历找到最大值，然后删除，再遍历，依次找到第2,3,4大的数据并且返回

每次都需要遍历一遍列表中所有的元素

快速排序的方法：将列表使用快速排序进行从大到小的排列，复杂度O（nlogn）然后直接返回对应的数，复杂度O（1），快速排序代码来自上一节。

代码如下所示：

# 直接遍历找到最大值，然后删除，再遍历，依次找到第2,3,4大的数据并且返回
def find_1_2_4(lis):
    find1=lis[0];find2=lis[0];find3=lis[0];
    for i in range(len(lis)):
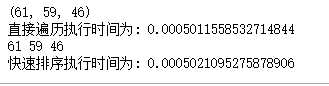
        if find1

实验结果如下图所示：

可见在数据量如此之小的情况下，时间相差无几，并不能反映出效率问题。

2)首先生成10000个随机数据，找出第4999小的数，如果直接使用排序算法，那么时间复杂度就是O（nlogn），然后直接输出第4999个数就行了。

但是我们可以使用分治策略对算法进行优化，使得算法的复杂度小于排序算法的O（nlogn）

算法步骤如下：

首先选取一个基点，比支点大的放支点右边，比支点小的放支点左边（到这里和快排一样），看看支点左边有多少个数，如果大于k-1说明在k在左边，左边递归，如果小于k-1说明在k右边，右边开始递归，并且新寻找的是k-pos小的数，如果相等，那么返回

代码如下：

# 寻找第k小的数的辅助函数
def k_find(lis, k):
    pivot = lis[len(lis)//2]
    
    left = 0
    right = len(lis)-1
    
    lis[0],lis[len(lis)//2]=lis[len(lis)//2],lis[0]
    while leftk:
        return k_find(lis[0:pos], k)
    else:
        return k_find(lis[pos:], k-pos)


if __name__ == "__main__":
    import random
    import cProfile
    
#     产生100000个随机数组
    num = 100000
#     array = [random.randint(1, 1000) for i in range(num)]
    array=[]
    a=1
    for i in range(num):
        a = a+random.randint(1,20)+1
        array.append(a)
    
    # 乱序操作
    random.shuffle(array)
    random.shuffle(array)
    
    import copy
    # 进行一个深度拷贝，用于测试
    arraycopy = copy.deepcopy(array)
    

#     用O(n)的算法得到第k小的数
    k=4999
    
    import time
    starttime= time.time()
    n = k_find(array, k)
    endtime=time.time()
    print("使用线性查找的时间为:",endtime-starttime)
    print("查找得到的数为:",n)

    starttime= time.time()
    quicksort(arraycopy, 0, len(arraycopy)-1)
    endtime=time.time()
    print("使用快排查找的时间为:",endtime-starttime)
    print("查找得到的数为:",arraycopy[k-1])

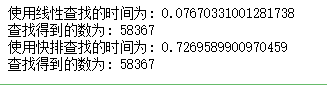
运行结果如下图所示：

查找到了相同的数字，然后发现效率竟然相差了十倍。

在这一版本的代码中，我们只要将代码中的

while pivot < lis[right]:
            right=right-1
        while left < right and (lis[left] < pivot or lis[left] == pivot):
            left=left+1

这一部分的大于号与小于号略作修改，即可用于解决第k大的数这一问题，即：

while pivot > lis[right]:
            right=right-1
        while left < right and (lis[left] > pivot or lis[left] == pivot):
            left=left+1

将修改后的代码用于求解leetcode上第215号题，成功通过

我实现的版本还是存在很多问题的，比如基准数的选择上，而且在出现相同数字的时候可能会出现问题，参考教科书上的解决方案还是很好的，取中间数的中间数，保证了效率，所以我照着书上敲了一遍代码（下面这个方案纯粹是照着敲上去的）

# 线性时间选择
lis1 = [4, 59, 7, 23, 61, 55, 46]

# 选择第k小的数的分治算法
def select_fct(array, k):
    if len(array) <= 10:  # 边界条件
        array.sort()
        return array[k]
    
    pivot = get_pivot(array)  # 得到数组的支点数
    array_lt, array_gt, array_eq = patition_array(array, pivot) # 按照支点数划分数组
    
    if k 0:
        num_medians +=1    # 不能被5整除，组数加1
        
    for i in range(num_medians):    # 划分成若干组，每组5个元素
        beg = i*subset_size
        end = min(len(array), beg+subset_size)
        subset = array[beg:end]
        subsets.append(subset)
    medians = []
    for subset in subsets:
        median = select_fct(subset, len(subset)//2)    # 计算每一组的中间数
        medians.append(median)
    pivot = select_fct(medians, len(subset)//2)    # 中间数的中间数
    return pivot
    
# 按照支点数划分数组
def patition_array(array, pivot):
    array_lt = []
    array_gt = []
    array_eq = []
    for item in array:
        if item < pivot:
            array_lt.append(item)
        elif item > pivot:
            array_gt.append(item)
        else:
            array_eq.append(item)
    return array_lt, array_gt, array_eq

import random
if __name__ == "__main__":
    import cProfile
    # 产生100个随机数组
    num = 100000
    array = [random.randint(1, 1000) for i in range(num)]
#     print(array)
    random.shuffle(array)
    random.shuffle(array)
    # 用O(n)的算法得到第k小的数
    k=15000
#     kval = select_fct(array, k)
    cProfile.run("select_fct(array, k)")
#     print(kval)

问题2，大数乘法问题。分别尝试计算9*9， 9999*9999, 9999999999*8888888888的结果
问题背景：
      所谓的大数相乘，就是指两个位数比较大的数字进行相乘，一般而言相乘的结果超过了进本类型的表示范围，所以这样的数不能够直接做乘法运算。
      其实乘法运算可以拆成两步，第一部，将乘数与被乘数逐位相乘，第二步，将逐位相乘得到的结果对应相加起来。
传统的大数乘法问题就是将数值的计算利用字符串来计算，从而解决位数溢出的问题。这种类型的以前曾经使用C++实现过。
然而我们现在要做的不是这个问题，我们的问题是请设计一个有效的算法，可以进行两个n位大整数的乘法运算，因为是nXn位的问题，解决方案偏向于定制化，我们需要的是将大数乘法O（n²）的复杂度降低，利用分治算法，将大的问题分解成为小的问题，先分，然而再合，从而优化解的方案。
代码实现：
前两个问题很简单，不再实现

9999999999*8888888888
对于这个问题，我们首先直接使用C++进行计算，结果肯定是有问题的
初次实验如图所示：

下面改用python语言 利用分治算法进行大数乘法的计算：

# 大数乘法
9*9
9999*9999
9999999999*8888888888

import math

# 计算符号
def sign(x):
    if x<0:
        return -1
    else:
        return 1
    
# 写一个计算大数乘法的函数 a和b是大数 计算他们俩相乘
def divideConquer(x, y, n):
    s = sign(x)*sign(y)
    x = abs(x)
    y = abs(y)

    if x==0 or y==0:    # 如果其中有一个为0 直接返回0
        return 0
    elif n==1:    # 递归结束条件 n=1
        return x*y*s
    else:
        A = x // math.pow(10, n//2)    # 获得第一个数的前半部分
        B = x - A*math.pow(10, n//2)    # 获得第一个数的后半部分
        C = y // math.pow(10, n//2)    # 获得第二个数的前半部分
        D = y - C*math.pow(10, n//2)    # 获得第二个数的后半部分
        AC = divideConquer(A, C, n//2)    # AC相乘的结果
        BD = divideConquer(B, D, n//2)    # BD相乘的结果
        ABCD = divideConquer(A-B, D-C, n//2)+AC +BD    # 计算中间量AD+BC的结果 实际的计算方式是(a-b)(d-c)+ac+db
        return s * (AC*math.pow(10, n)+ABCD*math.pow(10, n//2)+BD)
    
    print(A,B,C,D)

if __name__ =='__main__':
    print(int(divideConquer(9999999999,8888888888,10)))

在很快的时间之内就可以完成。

测试结果：

提出问题：是不是因为python的内部机制才使得计算这么快的呢？

于是重新进行了测试

if __name__ =='__main__':

    import cProfile
    cProfile.run("divideConquer(123456789123456789123456789123456789123456789123456789123456789123456789,123456789123456789123456789123456789123456789123456789123456789123456789,72)")
    cProfile.run("123456789123456789123456789123456789123456789123456789123456789123456789*123456789123456789123456789123456789123456789123456789123456789123456789")

这里使用了72位的数字

结果如图所示：

分治法的函数调用次数还是相当的多的

可是为什么直接用py内部的机制也是这么快呢？python到底是如何实现大数相乘的？查阅了相关资料之后发现，大整数乘法还可以采用FFT求循环卷积来实现，复杂度为O（nlogn）（网上这么说的，我也不知道对不对），然而python内部实现大整数相乘还是采用的是分治算法，理由是酱紫的：py日常计算的大整数不够大，所以还是用的是分治。