贝叶斯优化(BayesianOptimization)

贝叶斯优化

  这篇blog参考github上一个基于高斯过程回归的贝叶斯优化开源项目(python)：https://github.com/fmfn/BayesianOptimization

---

贝叶斯优化器的介绍

  贝叶斯优化在不知道目标函数（黑箱函数）长什么样子的情况下，通过猜测黑箱函数长什么样，来求一个可接受的最大值。和网格搜索相比，优点是迭代次数少(节省时间)，粒度可以到很小，缺点是不容易找到全局最优解。
  贝叶斯优化流程图如下：

  贝叶斯优化有两个核心过程，先验函数(Prior Function,PF)与采集函数(Acquisition Function,AC)，采集函数也可以叫效能函数(Utility Funtcion)，但一般还是称呼为采集函数，见下面引用论文A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning的话。PF主要利用高斯过程回归(也可以是其它PF函数，但高斯过程回归用的多)；AC主要包括EI，PI，UCB这几种方法，同时exploration与exploitation的平衡，也是通过AC来完成的。

The process of deciding where to sample next requires the choice of a utility function…To make clear which function we are discussing, we will refer to this utility as the acquisition function (also sometimes called the infill function)

---

采集函数(Acquisition Function,AC)

  常见的采集函数有下面三种，UCB，PI，EI，先介绍最好理解的UCB。

UCB(Upper confidence bound)

  $UCB=\mu (x)+k\sigma (x)$，k为调节参数，直观地理解为上置信边界。

PI(probability of improvement)

  $PI(x)=P(f(x)\ge f(x^{+})+\upsilon )=\Phi (\frac{\mu (x)-f(x^{+})-\upsilon }{\sigma (x)})$
  超参数$\upsilon$用于调节exploitation与exploitation，$\upsilon =0$更倾向于收敛到$f(x^{+})附近，$
$\Phi (\cdot )表示正态累计分布函数，f(x^{+})表示现有的最大值。$
  其原理就是找到未知点的函数值比$f(x^{+})$大的概率，取这些点中概率最大的点，具体比$f(x^{+})$大多少不考虑，这里通过Z-scores标准化法，让每个未知点函数值大于$f(x^{+})$的概率可以进行比较。
  Z-scores标准化法，$\frac{x-\mu }{\sigma }$，x为观察点，$\mu$为所有观察点的均值，$\sigma$为所有观察点标准差，$\frac{x-\mu }{\sigma }$的概率密度函数符合标准正态分布。

EI(Expected improvement)

$$EI(x)=\{\begin{array}{ll}(\mu (x)-f(x^{+}))\Phi (z)+\sigma (x)\Phi (z)& \sigma >0\\ 0& \sigma =0\end{array}$$
$$z=\frac{\mu (x)-f(x^{+})}{\sigma }$$
  $\Phi (\cdot )$为正态累计分布函数，$\varphi (\cdot )$为正态概率密度函数，$f(x^{+})$表示现有的最大值。
  EI函数解决了PI未考虑未知点，比已知最大点大多少的问题，EI函数求的是未知点函数值比$f(x^{+})$大的期望。具体推导过程需要看文献A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning。[我有空仔细看看在回来补上，当时大体看看没看懂。]

---

算法流程

$输入：$
$target:黑箱函数$
$x:自变量取值范围$
$Y:可以接受的黑箱函数因变量取值$
$输出：$
$x:贝叶斯优化器猜测的最大值的x值$
$target(xnew):贝叶斯优化器猜测的最大值的函数值$

伪代码：

def BayesianOptimization(target,x,Y):
    IF 初始化？
        Yes： 
            xold为已知的所有点中目标函数取得最大值的自变量值
            IF target(xold)>Y?     
                Yes:   return xold,target(xold)    #撞了大运，还没开始迭代就结束了
                No:    Pass
        No:  随机初始化
    While    target(xnew)

---

贝叶斯优化的一个模拟实验

  假设我们想知道下面这个黑箱函数在(-2,10)的最大值，$f(x)=e^{-(x-2{)}^2}+e^{\frac{-(x-6{)}^2}{10}}+\frac{1}{x^2+1}，$最大值大概是14，我们假定找到一个点其函数值大于13，就已经可以接受了，返回该函数值。

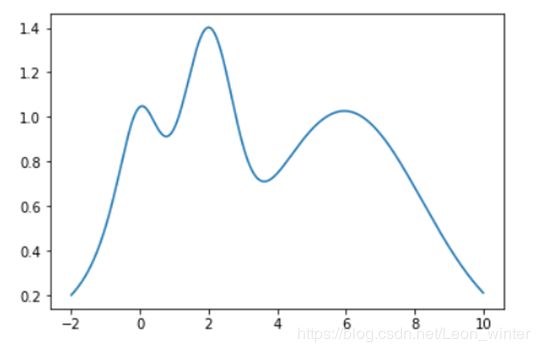
探索(exploration)与利用(exploitation)

  探索(exploration)：简单来说就是尽量选择远离已知点的点为下一次用于迭代的参考点，即尽量探索未知的区域，点的分布会尽可能的平均。
  利用(exploitation)：简单来说就是尽量选择靠近已知点的点为下一次用于迭代的参考点，即尽量挖掘已知点周围的点，点的分布会出现一个密集区域，容易进入局部最大。
  如下，上面的图表示贝叶斯优化器以利用为主，下面图表示贝叶斯优化器以探索为主。

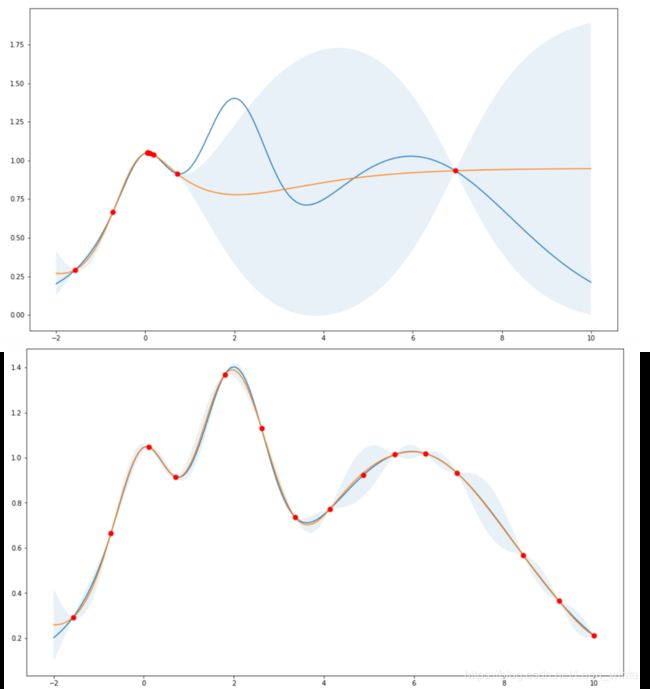
  在上文提到的github项目中，通过kappa这个参数平衡探索和利用，如上，上面的图kappa=0.1，下面的图kappa=10，我们下面的代码取kappa等于1.96，即$UCB=\mu (x)+1.96\sigma (x)$，github示例中kappa取的是中间值5，这里取1.96是为了让下面演示贝叶斯优化过程中，UCB就是95%置信区间的上界，更好理解UCB是什么，详细请看下面的贝叶斯优化过程。

贝叶斯优化过程

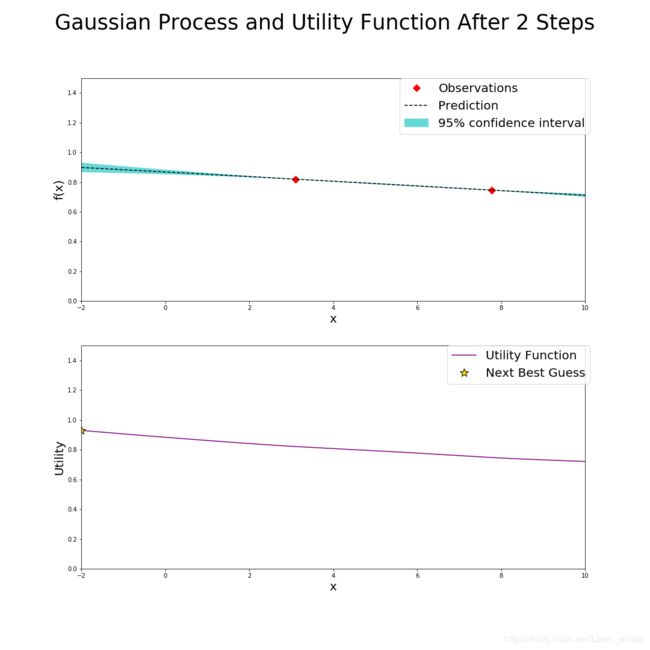
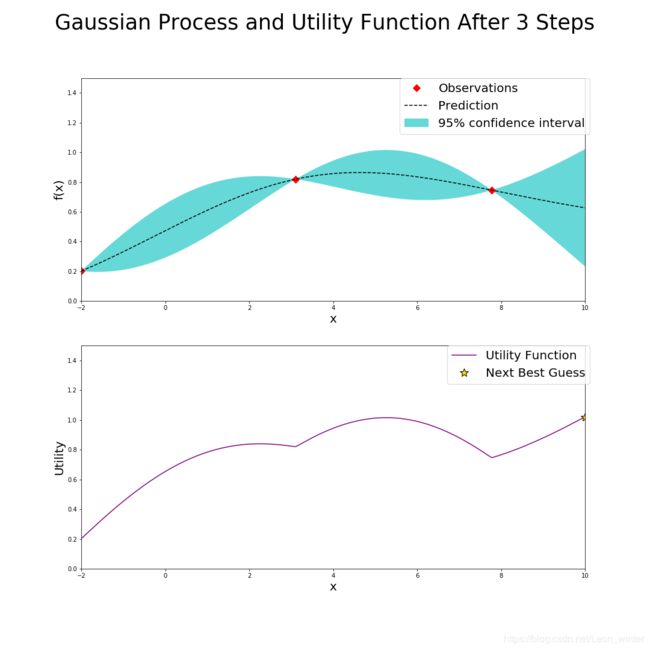
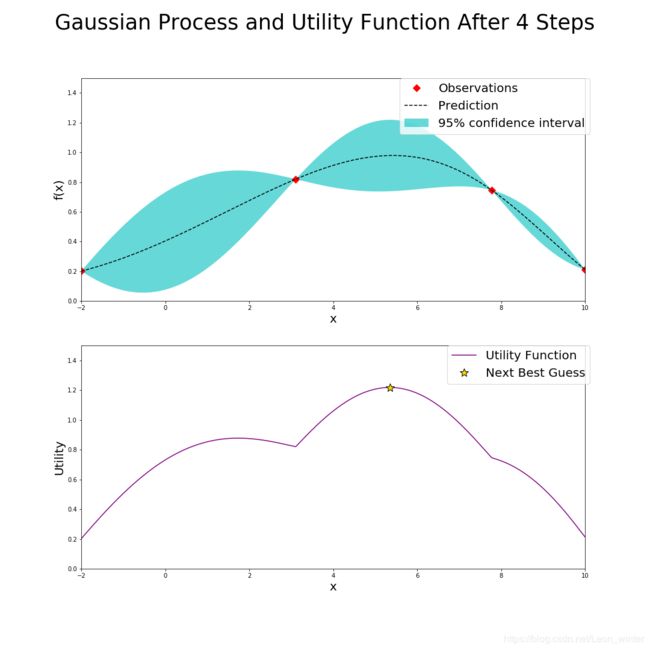
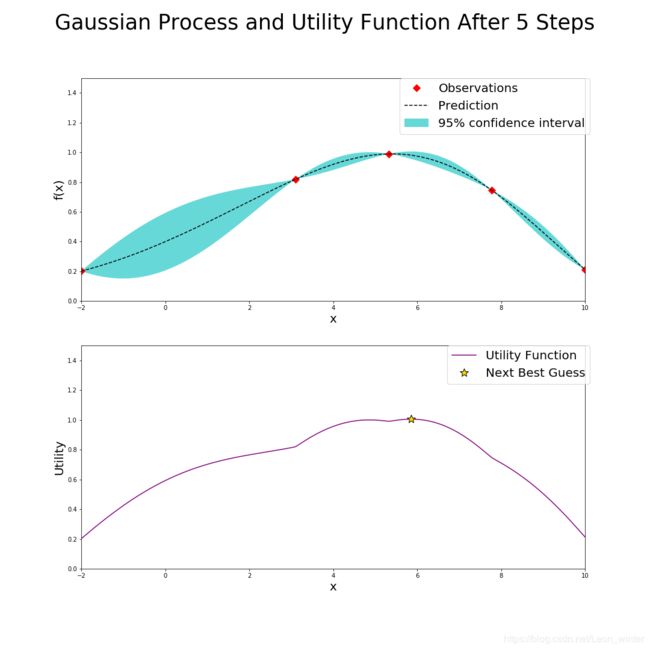
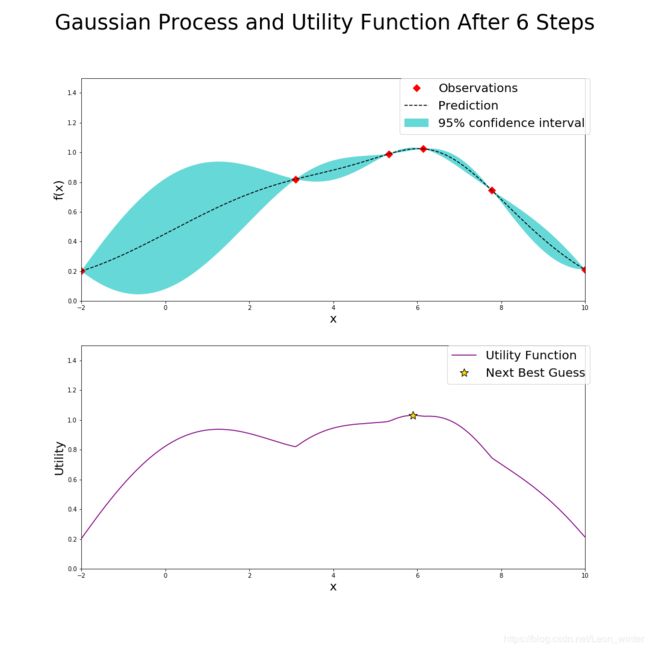
  下面第一个图产生的两个点(红点)其实是初始化过程产生的，和贝叶斯优化没有什么关系，为了方便分析，这里默认初始化的两个点也是贝叶斯优化前两次迭代过程产生的，也就是说，在经过几次迭代，即标题中的"After xxx Steps"，就有xxx个点的值显示在每次迭代的上面的图中(红点标注)，每次迭代的下面的图是根据UCB确定的。

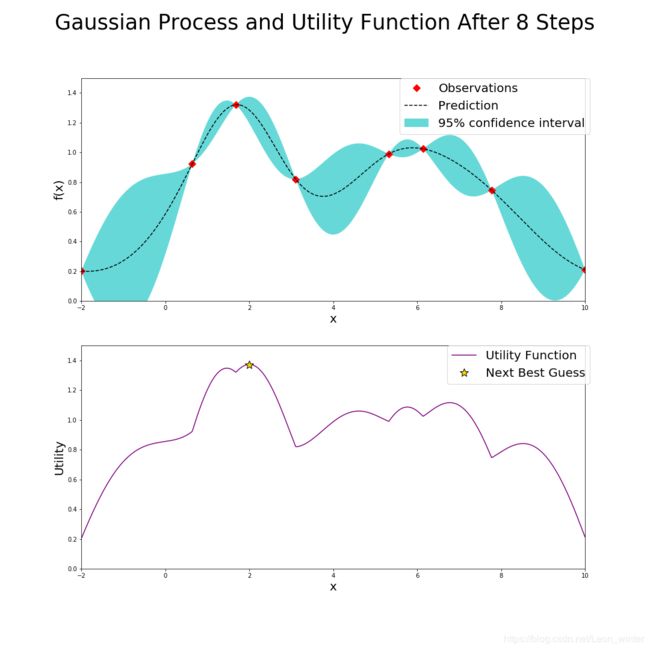
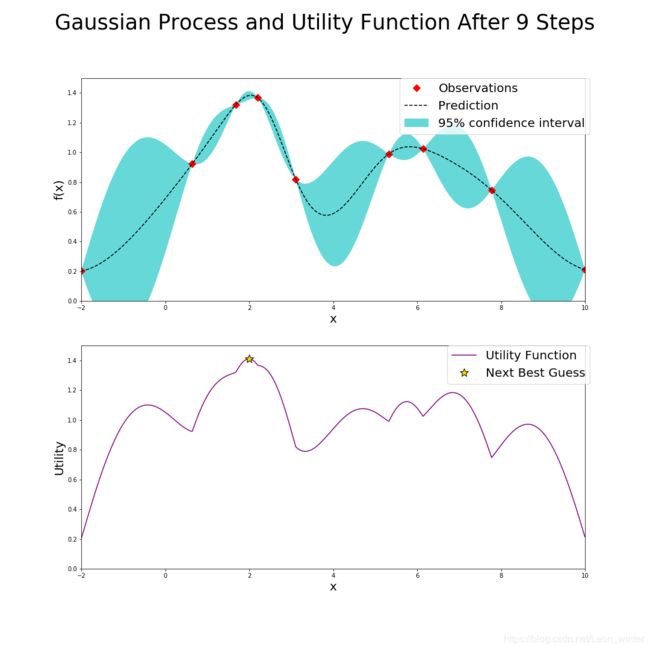
  看第9步迭代结果，可见第9步迭代结果就已经很接近真实的最大值，如果我们认为大于1.3的结果我们就可以接受，所以第9个确定的点就是可以接受的点，这时贝叶斯优化器就会退出迭代，把该点的值和函数值返回。
  与网格搜索相比较，贝叶斯优化器可以很快地确定一个可以接受的的值，这在求黑箱函数任意函数值的时间复杂度很高时，显得尤其的有优势，同时贝叶斯优化器没有搜索细度的限制。缺点是返回的结果不一定是真实的最大值(网格搜索也不一定能找到)。

  下面以第5次迭代到第6次迭代为例，讲解一下具体的步骤

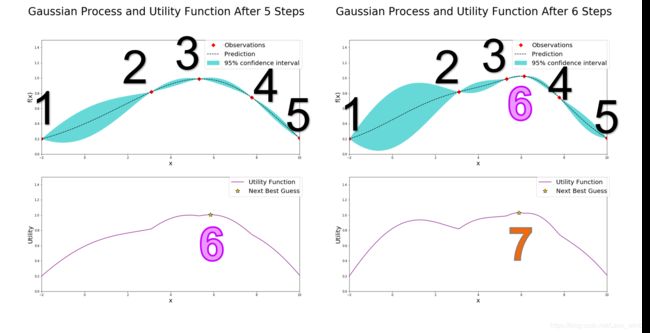
  如左上图，在经过了五次迭代后，左上图已经有五个确定的点(红点标出)，但是此时的最大的已确定点3达不到预期的要求(假设我们要求找到的点的函数值一定要大于1.3，不大于1.3就继续猜)，因此贝叶斯优化器需要根据已知的情况(五个确定的点)进一步猜测最大点在哪里，按照UCB策略，贝叶斯优化器就计算出左下的AC函数，AC函数图像我不说也能猜到，就是左上图中的蓝色边界上界，而AC函数最大值就是贝叶斯优化器猜的第六个点的位置，计算该点的函数值，看右上图，发现点6确实比点3好一点，但是还达不到要求，继续猜第7个点的位置，就是右下图新的AC函数取得最大值的位置。
  现在说一下左上图和右上图中的虚线和蓝色区间，虚线表示高斯回归过程求得的未知点的均值$\mu$，同时高斯过程也会给出未知点的标准差$\sigma$(和已知点相比，未知点太多了)，而蓝色区间就是$\mu \pm 1.96\sigma$，所以可见越是靠近已知点，标准差越小，越是远离已知点，标准差越大，此时说明高斯过程回归对这个未知点越不确定。
  95%的置信区间是$\mu \pm 1.96\sigma$，理解为未知点的均值落在$\mu \pm 1.96\sigma$区间内的概率为0.95(已经很高了)，关于置信区间计算，可以看Blog：https://blog.csdn.net/bitcarmanlee/article/details/82709774
  关于高斯过程回归，有空我在单独写一篇blog介绍。

---

贝叶斯优化的应用

  贝叶斯优化器用于调参，可以很快找到一个可以接受的超参数值，和网格搜索相比，优点是迭代次数少(节省时间)，粒度可以到很小，缺点是不容易找到全局最优解。例如我们想调logistic回归的正则化超参数，就把黑箱函数设置成logistic回归，自变量为超参数，因变量为logistic回归在训练集准确度，设置一个可以接受的黑箱函数因变量取值，例如0.95，得到的超参数结果就是可以让logistic回归分类准确度超过0.95的一个超参数。