最后一公里极速配送
最后一公里极速配送
Another url: https://bulihanjie.github.io/2016/09/22/最后一公里极速配送/
题目描述
https://tianchi.shuju.aliyun.com/competition/information.htm?spm=5176.100067.5678.2.nXeJox&raceId=231581
##成绩
第一赛季:第一名
第二赛季:第五名(前三名使用了作弊…)
总纲
题目中有两种包裹,分别是电商包裹和O2O包裹:
- 电商包裹:数量多,包裹数目大,路程较近,由124个网点配送;
- O2O包裹:数量较少,包裹数目小,路程较远,有时间窗口。
由于两种包裹的特性差异较大,如果对所有包裹一起考虑,很难得到一个满意的策略来对问题全局优化。所以在本方案中,两种包裹进行分开考虑,再对每种包裹的方案进行合并。总的方案流程图如下:
O2O包裹之费用流
在问题中,O2O包裹有配送时间和送达时间的限制,为了简化问题,使得问题更容易求解,有以下假设:
- 快递员在商家取一个O2O包裹后,下一个动作必定是把包裹送达用户手中。即快递员身上不同时存在两个O2O包裹;
- 快递员抵达商家的时间,不大于商家要求的取件的时间或超过的时间有个上限值。
基于假设,可以认为快递员在商家要求的区间时间收取O2O包裹,并且立即运送到相应的用户,与原问题相比少了时间窗口限制和容量的限制,容易得到的数学模型表达如下:
设n是O2O包裹数量,m是配送的快递员数量, 表示第i个O2O包裹, 表示第i个O2O包裹的取件时间。
相关二进制变量如下:
g i j = { 1 派 送 包 裹 i 后 派 送 包 裹 j 0 其 它 情 况 g_{ij}=\begin{cases}1& 派送包裹i后派送包裹j\\0& 其它情况\end{cases} gij={10派送包裹i后派送包裹j其它情况
最小化目标函数:
min f = ∑ i = 0 n ∑ j = 0 n g i j ∗ c o s t ( x i , x j ) + ∑ i = 0 n h a n d l e ( x i ) \mathop {\min }f=\sum_{i=0}^n\sum_{j=0}^ng_{ij}*cost(x_i,x_j)+\sum_{i=0}^nhandle(x_i) minf=i=0∑nj=0∑ngij∗cost(xi,xj)+i=0∑nhandle(xi)
s.t.
∣ { j ∣ ∑ i = 0 n g i j = 0 } ∣ = m \left|\left\{j \left.\right| \sum_{i=0}^ng_{ij}=0 \right\}\right|=m ∣∣∣∣∣{j∣i=0∑ngij=0}∣∣∣∣∣=m
∑ j = 0 n g i j ≤ 1 a n d g i j = 0 i ∈ [ 0 , n ) \sum_{j=0}^ng_{ij}\leq1\ and\ g_{ij}=0\ i\in[0,n) j=0∑ngij≤1 and gij=0 i∈[0,n)
c o s t cost cost是根据题目计算的两个O2O包裹间路程的耗时, h a n d l e handle handle是配送O2O包裹的耗时,容易得出公式的第二项是一个常数。
对于问题的求解,容易得出一个费用流的求解方法,有两个参数分别是派送的快递员数量 m m m和时间差 t l tl tl:
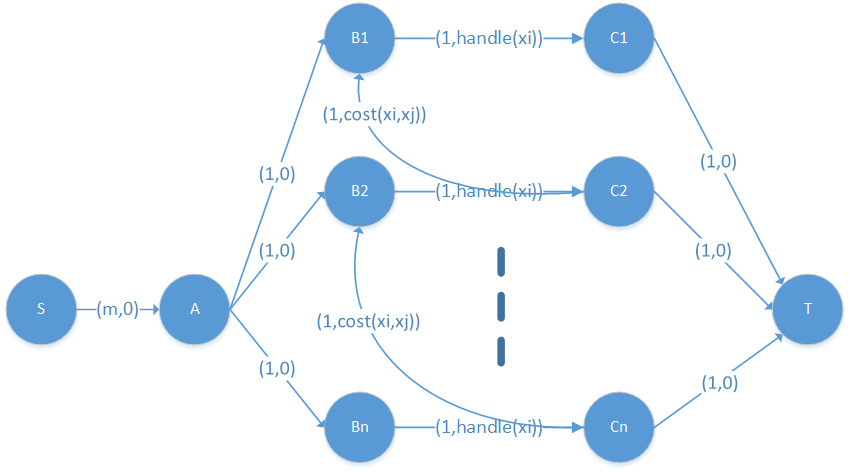
- 图中有一个起始顶点 S S S和终止顶点 T T T;
- 图中有一个顶点 A A A,限制派送包裹的快递员数量,起始点 S S S与顶点 A A A中有一条容量为m费用为0的弧;
- 每个包裹对应有两个顶点 B i B_i Bi和 C i C_i Ci,顶点 B i B_i Bi和 C i C_i Ci之间有一条容量为1费用为 10000 − h a n d l e ( x i ) 10000-handle(x_i) 10000−handle(xi)的弧,用来保证每个包裹只被派送一次,而费用加上一个很大的常数10000是为了保证每个包裹都被派送,每个包裹都加上相同的常数并不影响最小化目标函数的求解, h a n d l e ( x i ) handle(x_i) handle(xi)是派送包裹的耗时;
- 当包裹 i i i的取件时间不大于的送达时间 t l tl tl(送达时间是指在取件时间开始派送包裹 j j j,送到用户的时间), C i C_i Ci和 B i B_i Bi之间有一条容量为1费用为从包裹i用户赶往包裹 j j j商户的路上耗时。参数tl是为了有效的减少图的规模,并且在图中每个包裹只考虑了上一个包裹是从取件时间开始派送的,忽略了超时的可能性,适当的允许超时在 t l tl tl范围内能够取得更好的结果。
- 顶点 C i C_i Ci和终止顶点 T T T之间有一条容量为1费用为0的弧。
最后通过最大费用流的求解即可获得O2O包裹的配送方案,具体的示意图如图所示:
##O2O包裹之动态规划合并
通过费用流得出的O2O包裹配送方案,耗时较大,主要有以下原因:
- O2O的包裹较小,且路程较远,费用流的方法不能有效的利用快递员的运载量;
- O2O包裹的配送时限为90分钟,不需要立即送达,可以顺路配送相关的包裹。
所以,需要一种方案来尽量的合并O2O包裹减少耗时。
假设派送O2O包裹可以用序列 a 1 , a 2 , … … , a r a_1,a_2,……,a_r a1,a2,……,ar来表示,例如:派送一个O2O包裹E0000可以表示为E0000:1,E0000:-1,其中1代表取货,-1代表送达,序列表示取包裹E0000然后配送;派送包裹E0000和E0001的可能序列为E0000:1,E0001:1,E0000:-1,E0001:-1,序列表示取E0000包裹,然后取E0001包裹,依次配送E0000和E0001包裹。
当存在配送序列 a 1 , a 2 , … , a r a_1,a_2,…,a_r a1,a2,…,ar和配送序列 b 1 , b 2 , … , b t b_1,b_2,…,b_t b1,b2,…,bt,最少耗时的配送序列 c 1 , c 2 , … , c r + t c_1,c_2,…,c_{r+t} c1,c2,…,cr+t可以通过动态规划进行求解:
假设序列 a i a_i ai和 b i b_i bi在最优配送序列ci中,每个O2O包裹的配送顺序与原序列 a i a_i ai和 b i b_i bi相同,虽然此假设并不严谨但在大多数情况下是符合的,基于此假设能够得到动态规划快速求解的方法。
设 f i , j , k f_{i,j,k} fi,j,k为序列 a 1 , a 2 , … , a i a_1,a_2,…,a_i a1,a2,…,ai和序列 b 1 , b 2 , … , b j b_1,b_2,…,b_j b1,b2,…,bj合并为 c 1 , c 2 , … , c i + j c_1,c_2,…,c_{i+j} c1,c2,…,ci+j的最少耗时,其中i≤r,j≤t,k=0或1代表最后一个动作 c i + j c_{i+j} ci+j为 a i a_i ai或 b j b_j bj。
min f i , j , k = min { m i n ( f i − 1 , j , 0 + c o s t ( a i − 1 , a i ) , f i − 1 , j , 1 + c o s t ( a j , a i ) ) k = 0 a n d i ≠ 0 m i n ( f i , j − 1 , 0 + c o s t ( a i , a j ) , f i , j − 1 , 1 + c o s t ( a j − 1 , a j ) ) k = 1 a n d j ≠ 0 c o s t ( b 0 , . . . , b j ) + c o s t ( b j , a 0 ) k = 0 a n d i = 0 c o s t ( a 0 , . . . , a i ) + c o s t ( a i , 0 ) k = 1 a n d j = 0 \mathop {\min }f_{i,j,k}=\mathop {\min }\begin{cases}min(f_{i-1,j,0}+cost(a_{i-1},a_i),f_{i-1,j,1}+cost(a_j,a_i))& k=0\ and\ i\neq0\\min(f_{i,j-1,0}+cost(a_i,a_j),f_{i,j-1,1}+cost(a_{j-1},a_j))& k=1\ and\ j\neq0\\cost(b_0,...,b_j)+cost(b_j,a_0)& k=0\ and\ i=0\\cost(a_0,...,a_i)+cost(a_i,_0)& k=1\ and\ j=0\end{cases} minfi,j,k=min⎩⎪⎪⎪⎨⎪⎪⎪⎧min(fi−1,j,0+cost(ai−1,ai),fi−1,j,1+cost(aj,ai))min(fi,j−1,0+cost(ai,aj),fi,j−1,1+cost(aj−1,aj))cost(b0,...,bj)+cost(bj,a0)cost(a0,...,ai)+cost(ai,0)k=0 and i̸=0k=1 and j̸=0k=0 and i=0k=1 and j=0
计算过程中 f i , j , k f_{i,j,k} fi,j,k需要判断序列的包裹合法和相应的路程时间。
由此可以得到一个有效的贪心策略:
- 假设参数 t t t;
- 选取两个包裹a和b,计算 c o s t ( a b ) − c o s t ( a ) − c o s t ( b ) cost(a^b)-cost(a)-cost(b) cost(ab)−cost(a)−cost(b),选取 c o s t cost cost增加最少且增加的 c o s t < t cost<t cost<t的两个包裹进行合并为新的包裹;
- 当任意两个包裹合并增加的 c o s t > t cost>t cost>t结束,否则从步骤2开始进行。
此策略能够有效的合并O2O包裹,提交的方案中选取15,O2O包裹最终的数量<1000。
最后通过费用流的方法进行最后的包裹配送规划。
##电商包裹之初始化
问题中,电商包裹又124个网点进行配送,且124个网点配送的范围并不重叠。所以不同网点的电商包裹分开考虑,同时也为了减少时间的复杂度。
对于不同网点的包裹配送方案初始化如下:
假设所有的电商包裹都是单独配送并且返回网点。选取任意两个电商包裹一起配送,时间消耗减少了网点分别配送两个包裹的路程耗时,时间消耗增加了两个包裹配送点之间的路程耗时。选取减少消耗最多且满足快递员容量限制的两个包裹一起配送。直至没有包裹可以一起配送为止。
##电商包裹之遗传算法
通过遗传算法能够一定程度上减少电商包裹的耗时,但相对于整个算法并不那么重要。遗传算法中加入初始化的结果作为某一条基因组,是为了结果能够更快的收敛。
编码方式:长度为n的编码,每一位记录下一个运送的电商包裹的编号,-1记录返回网点;
适应度函数:cost(电商包裹);
选择函数:1/适应度;
基因交叉:选择两条基因组,随机选择基因第i位交叉。由于要满足每个电商包裹只能配送一次,基因组中可能存在第j位与第i位是同样的数值,继续在第j位进行交叉,直至基因组合法为止;
基因突变:随机选取某一位设为-1。
##电商包裹之局部搜索
通过局部搜索的方法,相比遗传算法能更快更好的减少电商包裹的耗时,但是在电商包裹和O2O包裹合并的过程中没有得到一个很好的结果。所以最终是采用遗传算法。
所有的包裹按照初始化,可以按照配送的顺序排成一行 ,相应的最小耗时可以用动态规划来计算。枚举 i , j i,j i,j,把 a i a_i ai插入到序列的第 j j j位,计算相应的耗时。选取最小耗时的序列保存下来,重复插入的操作直至耗时不能减少为止。
序列 a i a_i ai的最小耗时计算如下:
设 f i f_i fi记录 c o s t ( a 1 , a 2 , . . . , a i ) cost(a_1,a_2,...,a_i) cost(a1,a2,...,ai)的最小耗时,状态转移如下: f i = m i n { f j + c o s t ( a j , a j + 1 , . . . , a i ) ∣ j < i , ∑ k = i j p a c k ≤ 140 } f_i=min\{f_j+cost(a_j,a_{j+1},...,a_i)|j<i,\sum_{k=i}^jpac_k\le140\} fi=min{fj+cost(aj,aj+1,...,ai)∣j<i,∑k=ijpack≤140},即枚举第 j j j到 i i i的电商包裹作为连续配送的一个子序列。
##背包合并
当O2O包裹合并以后,依然会有取货时间前的一段时间可以配送电商包裹,电商包裹经过合并之后得到了多个包裹的配送序列。所以主要是在配送O2O包裹前选择适合的电商包裹序列配送。
假设配送O2O包裹的起始时间为 s t i st_i sti,电商包裹配送序列的耗时为 c i c_i ci,算法的流程如下:
- 枚举每个O2O包裹 y i y_i yi,起始时间为 s t i st_i sti;
- 枚举电商包裹配送序列 x i x_i xi所谓配送O2O包裹前最后配送的电商包裹;
- 剩余时间 t = s t i + c o s t ( x i , y i ) t=st_i+cost(x_i,y_i) t=sti+cost(xi,yi),cost代表配送完电商包裹然后配送O2O包裹的路程耗时,减去配送完电商包裹返回网点的耗时;
- 对剩余时间t进行网点与 相同的电商包裹序列填充,这里可以用01背包。但是考虑到有些快递员只配送电商包裹,所以考虑每个电商包裹序列的价值为:电商包裹序列耗时-网点到最后一个配送点的路上耗时,能够获得更好的方案。
- 删除所有选择的电商包裹序列;
- 重复以上步骤,直至枚举所有的O2O包裹。
- 对剩余的O2O包裹用空闲的快递员进行配送
##尝试
比赛中有各种尝试:
- 费用流中加入预测评估使得O2O包裹的起始时间能更好的合并电商包裹
- O2O包裹和电商包裹在DP Merge中一起合并
各种尝试中会增加算法的复杂度,但是提高的成绩并不明显,因此也不再描述了。
##总结
总的来说,方案中采用的是O2O包裹和电商包裹分开的计算的方法。O2O包裹合并之后能够有效的对O2O包裹进行配送。我认为本方案的优点在于:算法运行的速度快,能够很快的得出结果,思路也是比较的简单的。而方案中比较不足的在于:O2O包裹和电商包裹不能很好的进行融合,而且在单独配送电商包裹的策略中没有很好的考虑O2O包裹的取件时间。
在后面经过对方案的统计分析,即使把方案中的电商包裹策略做的更加完善也不能提高很多,因此后面的工作主要着重于如何真正的把电商包裹和O2O包裹融合起来。但是考虑到时间复杂度等问题,最终没有得到一个很好的解决方案,不能不是一个遗憾。
##答辩总结
比赛中第一赛季第一名,第二赛季第五名。在第二赛季中有意思的是在最后几天不断被反超了,而且分数的差距非常大,所以答辩也是抱着学习的心态去的。
但是前三名的成绩是利用了题目10次作弊的限制,而且官方的评测程序计算耗时是根据提交结果的上一个时间计算,所以快递员配送过程中10次瞬移能得到更好的结果(第一赛季没多大用,第二赛季很多超时的O2O包裹所以提升会非常大)。其实这是很不合理的,但是阿里默认这种解释,即使不爽也没办法的了。
答辩过程中也能看到些其它的方法,也有所启发吧,不过毕竟不是研究这领域的,也不打算研究下去了。