NumPy实现简单的神经网络分析Mnist手写数字库（四）之建立神经网络

建立神经网络

引言

在上一节-划分迷你批(mini-batch)
中，我们将数据集划分为了大小相同的迷你批，便于之后采用迷你批梯度下降（mini-batch Gradient Descent）
对网络模型进行训练。在此之前，我们先建立一个网络，初始化网络中的参数。

神经网络简介

目的

为了建立一个参数控制的输入和输出之间的映射关系。这个映射关系往往是非线性的非常复杂的。
例如输入Mnist数据库的图像数据（784个float32类型数据）和输出图像中的数字（1个uint8类型数据）。
显然，要使用一个清晰函数表达式来描述这种复杂映射十分艰难。
但是不论多么复杂的映射关系，使用待定系数法和复杂度足够大的函数形式就一定可以来表达。
神经网路就是这样的一个含有诸多待定系数的复杂函数。

结构

神经网络算法的结构由许多层（layer）的神经元（Neuron）组成。

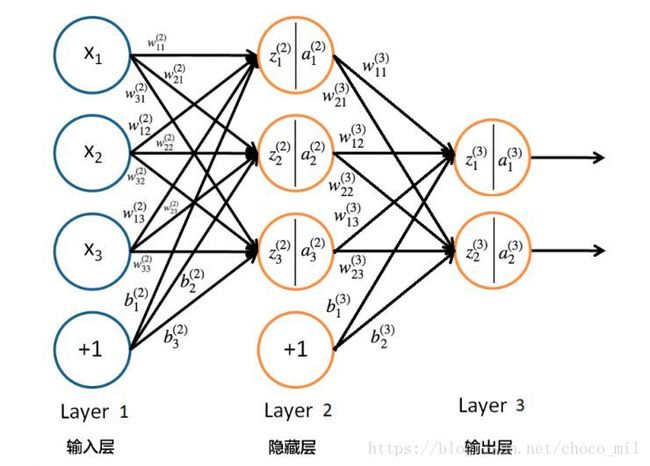
其中的箭头代表线性运算。
$$z_i^{[l{]}^{\prime }}=w_{ij}^{[l]}\cdot a_j^{[l-1]}$$
式中各量的上标代表层数，下标代表层中的序号。例如 $z_i^{[l]}$ 代表第l层中的第i个z。
而 $w_{ij}^{[l]}$ 则表示l层中的第i行第j列的权重（weight），第i行代表输出的对象是第i个，第j列代表输入是第j个。

+1代表偏置（bias），相当于线性函数中的常数项。是一个可以学习的参数。
加上偏置的完整线性运算
$$z_i^{[l]}=w_{ij}^{[l]}\cdot a_j^{[l-1]}+b_i^{[l]}$$

其中有竖线的圆代表神经元。竖线把圆一分为二，代表神经元对线性结果 $z_i^{[l]}$
做了非线性变换得到非线性结果$a_i^{[l]}$。此处的非线性函数又叫激活函数（activation function）。
常用的有sigmoid函数，tanh函数和ReLU（restricted linear unit）函数，在输出层往往还会用到softmax函数。
函数具体表达式大家可以自行查阅。在NumPy中基本都有现成的库函数可供使用。
$$a_i^{[l]}=g^{[l]}(z_i^{[l]})=g^{[l]}(w_{ij}^{[l]}\cdot a_j^{[l-1]}+b_i^{[l]})$$
这样便得到了一个简单的参数控制的非线性函数。而神经网络的精妙之处，就在于它是由很多这样的简单结构堆砌而成的，
从而得到一个复杂的函数。大家可以尝试把一个图上的神经网络去掉中间变量，展开成输出和输入的映射，想必是有点复杂的。
这还仅仅只有两层（不算输入层），大型的网络能达到成百上千层，复杂度令人咋舌。

初始化网络结构和参数

网络结构

一个稠密连接（两层直接的神经元两两相连）的网络结构由每层中的神经元个数决定。

在Python中，我们可以使用一个列表存储从输入到输出的每层神经元个数。

layers_size = [784, 20, 10]

代表一个输入有784个特征量，隐层有20个神经元，输出有10路的神经网络。

除去输入层（除去输入层是因为输入层是给定的样本，没有参数），一共有2层。一共有2个W（权重）和2个b（偏差）
要进行初始化。

初始化参数

初始化分为两个步骤：

1.建立正确维度的矩阵

2.赋予正确的初始值

首先新建一个Python文件

"""
parameters_initializer.py

初始化神经网络参数
"""

import numpy as np

建立正确维度的矩阵

$W^{[l]}$ 的维度为[layers_size[l],layers_size[l-1]]，注意输出对应行，输入对应列。

def initialize_parameters(layers_size):
    """
    初始化神经网络参数

    参数:
        layers_size -- 输入层、隐层、输出层的神经元个数，整型的列表

    返回:
        parameters -- 包含参数的字典, {"Wl": Wl, "bl": bl}
    """
    #求网络长度，不算输入层
    num_layers = len(layers_size) - 1

    #建立存储参数的字典
    parameters = {}

    #初始化权重和偏置
    for l in range(num_layers):
        parameters["W" + str(l+1)] = \
        initialize_weights(layers_size[l+1], layers_size[l])
        parameters["b" + str(l+1)] = \
        initialize_bias(layers_size[l+1], layers_size[l])

    return parameters

其中的函数initialize_weights()和initialize_bias()是给参数赋初始值的。稍后给出定义。

初始化参数

初始化权重

对于W，我们使用initialize_weights()

def initialize_weights(size_this, size_last):
    """
    初始化一层中的权重
    使用He等人发明的初始化方法:
        np.random.randn(size_this, size_last) * 2.0 / size_last
        size_last 是上一层的大小

    参数:
        size_this -- 本层的大小，整型
        size_last -- 上层的大小, 整型

    返回:
        weights -- 初始化后的参数
    """
    weights = np.random.randn(size_this, size_last) * 2.0 / size_last

    return weights

几点说明：

1.一定不能把权重全赋0。因为假如一层中的所有神经元参数都一样，因为输入相同，那么它们的输出就相同，
在之后的反向传播优化模型时，优化程度也一样。这就产生了一个层的神经元同步的现象。那就相当于一层所有的
神经元都在做相同的工作，也就相当于是只有一个神经元。整个网络就变成了“一根线”，大大降低了模型的学习能力，
还占用了很大的存储空间和运算资源。因此使用高斯随机数赋值。

2.使用He等人的初始化方法，对权重的高斯分布进行调整，能有效避免梯度爆炸/消失的问题。

3.所谓梯度爆炸和消失，就是当权重普遍大于1或小于1时，在较深的网络中，信息在网络中正向或反向传播时多次乘以大于1或
小于1的权重，导致结果过大或过小，导致值溢出或收敛速度过慢的问题。

4.通过对高斯分布进行调整，能使得初始权重整体上不偏向大于1或小于1。

初始化偏置

对于b，我们使用initialize_bias()

def initialize_bias(size_this, size_last):
    """
    初始化一层中的偏置
    为了避免死神经元的情况，我们初始化偏置为较小值(0.1):
        np.zeros(size_this, size_last) + 0.1

    参数:
        size_this -- 本层的大小，整型
        size_last -- 上层的大小，整型

    返回:
        bias -- 初始化后的偏置
    """
    bias = np.zeros((size_this, 1)) + 0.1

    return bias

一点说明：

1.在神经网络中，最常用的激活函数就是ReLU。

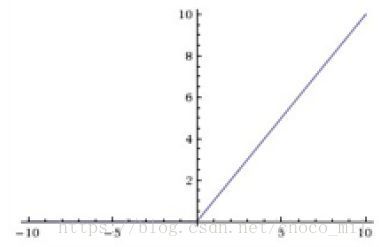
神经元只有在大于零的时候才会被激活（有输出）。给一个小的偏置，就是避免训练前期
大量的神经元都处于死寂状态。

调用函数

parameters = initialize_parameters(layers_size)

得到一个参数字典，这样就可以进行下一步的正向传播啦。

小节

在本节中，我们完成了对神经网络结构和参数的初始化，并做到了对网络结构的自适应。
在下一节中，我们将进行网络的正向传播。