程序员那些必须掌握的排序算法——下半部分
接着上一篇的排序算法,我们废话不多说,直接进入主题。
1.快速排序
快速排序(Quicksort)是对冒泡排序的一种改进。
快速排序由C. A. R. Hoare在1960年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
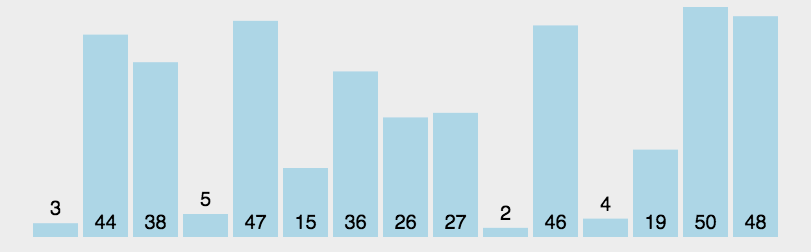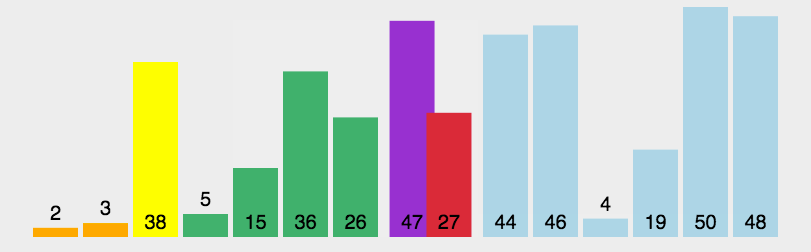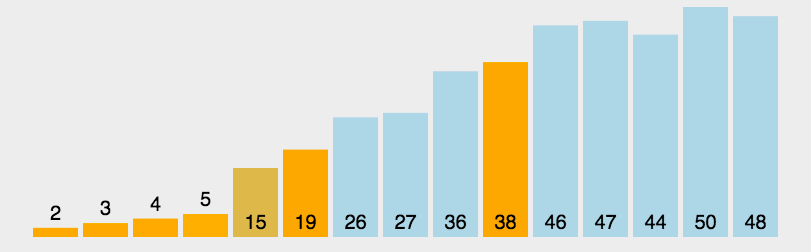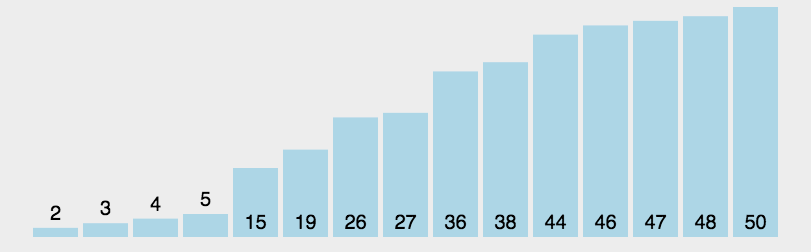
演示:
代码如下:
public static void quickSort(int[] arr, int left, int right) {
int l = left;// 左下标
int r = right;// 右下标
int pivot = arr[(left + right) / 2];// 找到中间的值
// 将比pivot小的值放在其左边,比pivot大的值放在其右边
while (l < r) {
// 在pivot左边寻找,直至找到大于等于pivot的值才退出
while (arr[l] < pivot) {
l += 1;// 将l右移一位
}
// 在pivot右边寻找,直至找到小于等于pivot的值才退出
while (arr[r] > pivot) {
r -= 1;// 将r左移一位
}
if (l >= r) {
// 左右下标重合,寻找完毕,退出循环
break;
}
// 交换元素
int temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
//倘若发现值相等的情况,则没有比较的必要,直接移动下标即可
// 如果交换完后,发现arr[l]==pivot,此时应将r左移一位
if (arr[l] == pivot) {
r -= 1;
}
// 如果交换完后,发现arr[r]==pivot,此时应将l右移一位
if (arr[r] == pivot) {
l += 1;
}
}
// 如果l==r,要把这两个下标错开,否则会出现无限递归,导致栈溢出的情况
if (l == r) {
l += 1;
r -= 1;
}
// 向左递归
if (left < r) {
quickSort(arr, left, r);
}
// 向右递归
if (right > l) {
quickSort(arr, l, right);
}
}
测试代码:
public static void main(String[] args) {
int[] arr = { 3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48 };
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
运行结果:
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
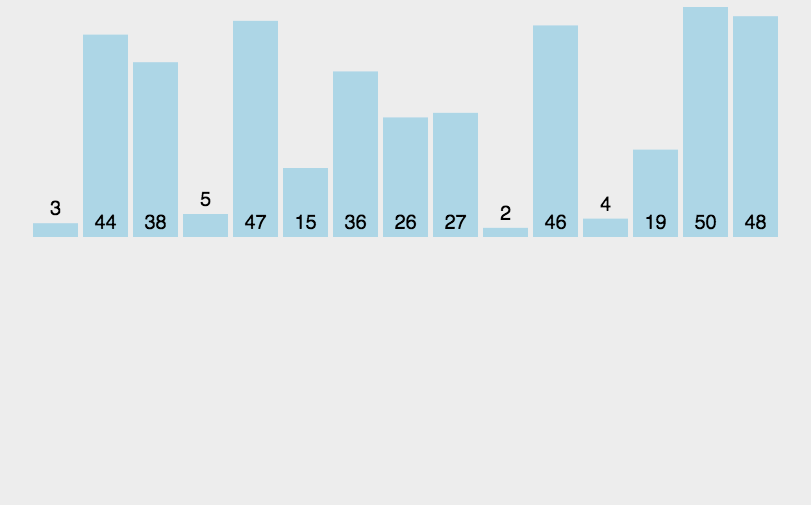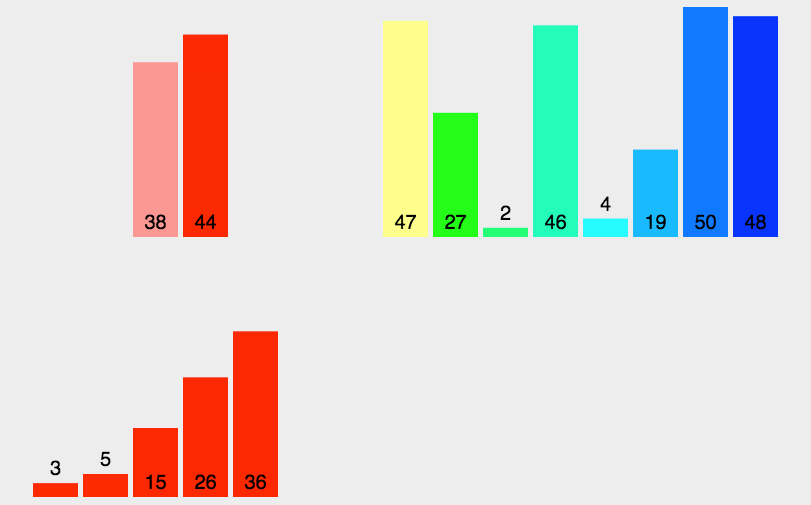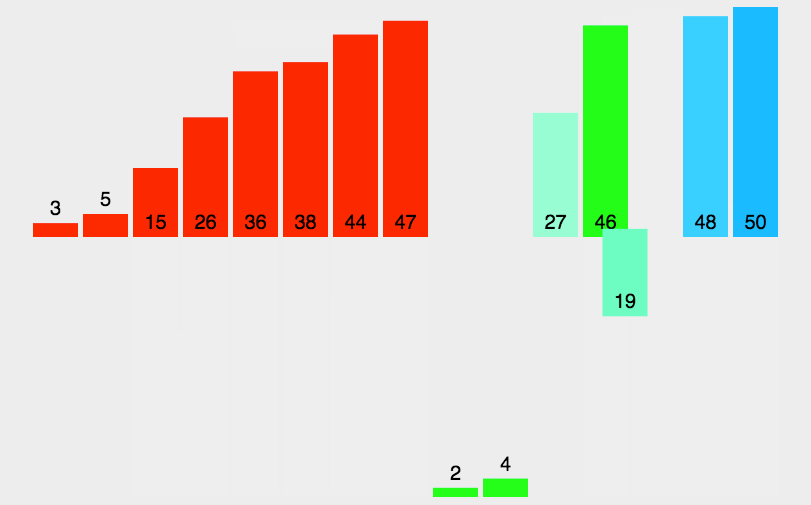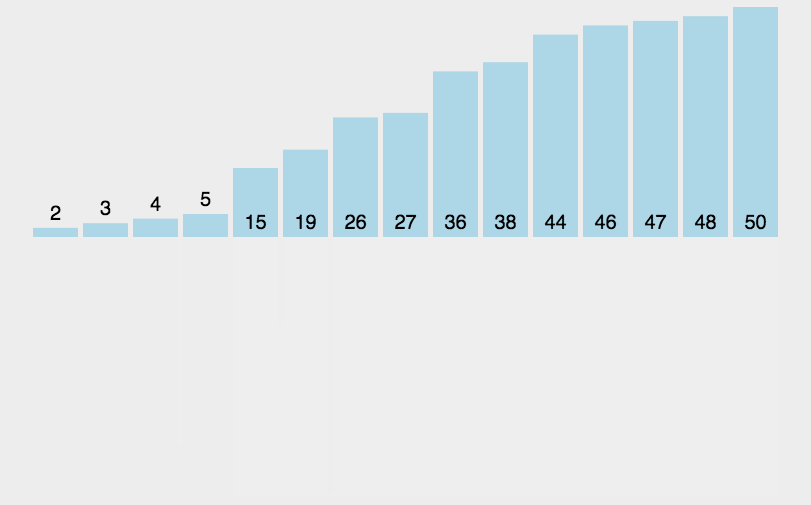
快速排序的实现原理很简单,就是将原数组分成两部分,然后以中间值为标准,比它小的就放其左边,比它大的就放其右边,然后在左右两边又以相同的方式继续排序。
所以在代码实现过程中,首先要创建两个移动的变量,一个从最左边开始往右移动,一个从最右边开始往左移动,通过这两个变量来遍历左右两部分的元素。当发现左边有大于中间数的元素,右边有小于中间数的元素,此时就进行交换。当两个变量重合也就是相等的时候遍历结束,然后左右两部分作递归处理。
2.归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
演示:
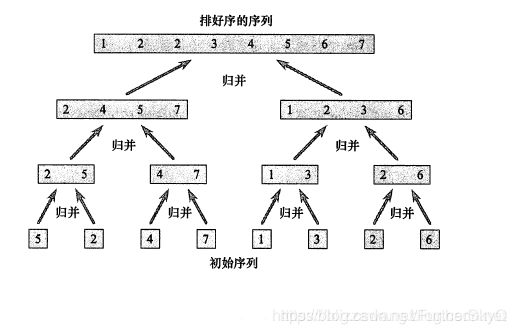
归并排序使用了一种分治思想,分治思想的意思就是’分而治之",就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单地直接求解。
通过这个动图来看的话,相信很多人都一脸懵,没关系,我们通过静态图来分析一下:
假设现在有一个待排序的序列,[5,2,4,7,1,3,2,2],那么我们就需要将该序列进行分治,先将其分成两份:[5,2,4,7]和[1,3,2,2],再将这两份分别分成两份:[5,2]和[4,7];[1,3]和[2,2],最后将这四部分再次分别分为两份,最后就将整个序列分为了八份。需要注意的是,在分的过程中,不需要遵循任何规则,关键在于归并,归并的过程中便实现了元素的排序。
代码如下:
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
// 分解
if (left < right) {
int mid = (left + right) / 2;// 中间索引
// 向左递归进行分解
mergeSort(arr, left, mid, temp);
// 向右递归进行分解
mergeSort(arr, mid + 1, right, temp);// mid + 1,中间位置的后一个位置才是右边序列的开始位置
// 每分解一轮便合并一轮
merge(arr, left, right, mid, temp);
}
}
/**
* 合并的方法
*
* @param arr 待排序的数组
* @param left 左边有序序列的初始索引
* @param right 中间索引
* @param mid 右边有序序列的初始索引
* @param temp 做中转的数组
*/
public static void merge(int[] arr, int left, int right, int mid, int[] temp) {
int i = left; // 初始化i,左边有序序列的初始索引
int j = mid + 1;// 初始化j,右边有序序列的初始索引(右边有序序列的初始位置即为中间位置的后一个位置)
int t = 0;// 指向temp数组的当前索引,初始为0
// 先把左右两边的数据(已经有序)按规则填充到temp数组
// 直到左右两边的有序序列,有一边处理完成为止
while (i <= mid && j <= right) {
// 如果左边有序序列的当前元素小于或等于右边有序序列的当前元素,就将左边的元素填充到temp数组中
if (arr[i] <= arr[j]) {
temp[t] = arr[i];
t++;// 索引后移
i++;// i后移
} else {
// 反之,将右边有序序列的当前元素填充到temp数组中
temp[t] = arr[j];
t++;// 索引后移
j++;// j后移
}
}
// 把有剩余数据的一边的元素填充到temp中
while (i <= mid) {
// 此时说明左边序列还有剩余元素
// 全部填充到temp数组
temp[t] = arr[i];
t++;
i++;
}
while (j <= right) {
// 此时说明左边序列还有剩余元素
// 全部填充到temp数组
temp[t] = arr[j];
t++;
j++;
}
// 将temp数组的元素复制到原数组
t = 0;
int tempLeft = left;
while (tempLeft <= right) {
arr[tempLeft] = temp[t];
t++;
tempLeft++;
}
}
关于归并排序的算法思想确实比较绕,所以我也在代码中写了很多注释。
我们先来测试一下:
public static void main(String[] args) {
int[] arr = { 3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48 };
int[] temp = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, temp);
System.out.println(Arrays.toString(arr));
}
运行结果:
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
来分析一下吧,对于该排序算法,有两个部分组成,分解和合并。首先讲讲分解,在前面也说到了,我们需要将待排序的序列不停地进行分解,通过两个索引变量控制,一个初始索引,一个结尾索引。只有当两索引重合才结束分解。此时序列被分解成了十五个小份,这样分解工作就完成了。接下来是合并,合并操作也是最麻烦的,也是通过两个索引变量i,j。开始i在左边序列的第一个位置,j在右边序列的第一个位置,然后就是寻找左右两个序列中的最小值,放到新序列中,这时可能会出现一边的元素都放置完毕了,而另外一边还存在元素,此时只需将剩余的元素按顺序放进新序列即可,因为这时左右两边的序列已经是有序的了,最后将新序列复制到旧序列。这里也特别需要注意,因为合并的过程是分步的,而并非一次合并完成,所以数组的索引是在不断变化的。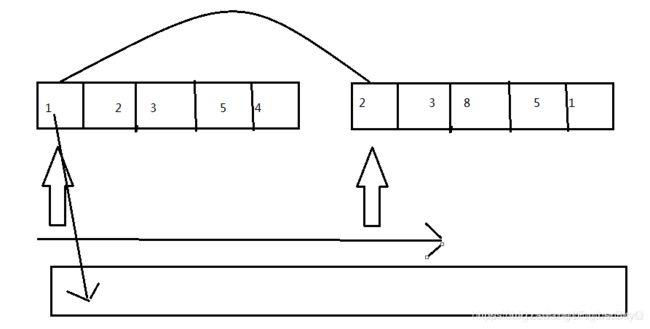
自己手动画了个图,左右两个箭头就是索引变量i,j,当i所指的元素也就是1和j所指的元素也就是2进行比较,发现1小,就将1放到新数组的第一个位置,此时应该将i和新数组的索引都右移一位,然后继续比较,以此类推,相信这样大家应该能理解了吧。
3.基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O(nlog( r )m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。基数排序是用空间换时间的经典算法。
演示:
基数排序的基本思想是:
将所有待比较的数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序,这样从最低位排序一直到最高位排序完成以后,数列就变为了一个有序序列。
这样说可能过于抽象,我们通过详细步骤来分析一下:
我们假设有一个待排序数组[53,3,542,748,14,214],那么如何使用基数排序对其进行排序呢?
首先我们有这样的十个一维数组,在基数排序中也叫桶。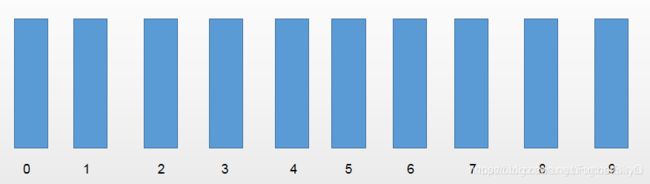
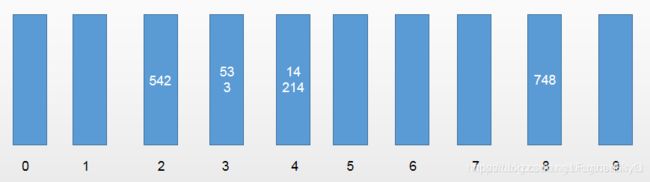
那么第一轮排序开始,我们依次遍历每个元素,并得到元素的个位数。拿到的第一个元素为53,其个位数为3,所以将53放入编号为3的桶中,第二个元素3的个位数也是3,所以也放在编号为3的桶中,而第三个元素542的个位数为2,所以将542放入编号为2的桶中,以此类推。
所以结果为:
将元素全部放入桶中之后,我们需要按照桶的顺序(也就是一维数组的下标)依次取出数据,并放回原来的数组。
那么很简单,按顺序取出数据并放回原数组之后,原数组将变为[542,53,3,14,214,748]。
这样第一轮就完成了,接下来开始第二轮。
第二轮排序和第一轮类似,也要去遍历数组元素,但不同的是第二轮的存放顺序取决于十位数。
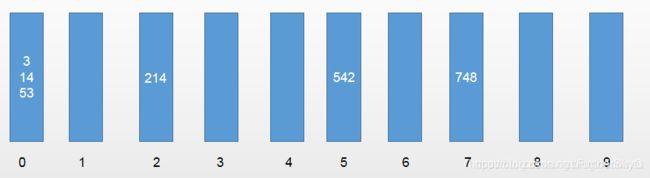
取出数据的第一个元素为542,十位数为4,所以放入编号为4的桶;第二个元素53,十位数为5,所以放入编号为5的桶;第三个元素3,十位数为0,所以放入编号为0的桶,以此类推。
所以结果为: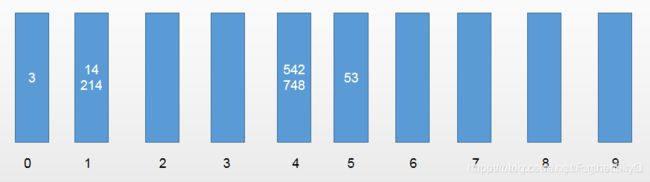
将元素全部放入桶中之后,我们需要按照桶的顺序(也就是一维数组的下标)依次取出数据,并放回原来的数组。
那么很简单,按顺序取出数据并放回原数组之后,原数组将变为[542,53,3,14,214,748]。
这样第一轮就完成了,接下来开始第二轮。
第二轮排序和第一轮类似,也要去遍历数组元素,但不同的是第二轮的存放顺序取决于十位数。
取出数据的第一个元素为542,十位数为4,所以放入编号为4的桶;第二个元素53,十位数为5,所以放入编号为5的桶;第三个元素3,十位数为0,所以放入编号为0的桶,以此类推。
所以结果为: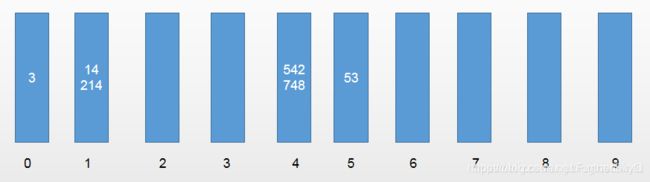
然后同样按照桶的顺序将数据从中取出并放入原数组,此时原数组变为[3,14,214,542,748,53]。
接下来又进行第三轮排序,以元素的百位数进行区分,结果为:
按顺序取出数据后,原数组变为[3,14,53,214,542,748]。这时的数组已经完成排序。
从中我们也可以知道,基数排序的排序轮数取决于数组元素中最大位数的元素。
代码如下
public static void raixSort(int[] arr) {
// 第一轮(针对每个元素的个位进行排序处理)
// 定义一个二维数组,模拟桶,每个桶就是一个一维数组
// 为了防止放入数据的时候桶溢出,我们应该尽量将桶的容量设置得大一些
int[][] bucket = new int[10][arr.length];
// 记录每个桶中实际存放的元素个数
// 定义一个一维数组来记录每个桶中每次放入的元素个数
int[] bucketElementCounts = new int[10];
for (int j = 0; j < arr.length; j++) {
// 取出每个元素的个位
int digitOfElement = arr[j] % 10;
// 将元素放入对应的桶中
// bucketElementCounts[digitOfElement]就是桶中的元素个数,初始为0,放在第一位
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
// 将桶中的元素个数++
// 这样接下来的元素就可以排在前面的元素后面
bucketElementCounts[digitOfElement]++;
}
// 按照桶的顺序取出数据并放回原数组
int index = 0;
for (int k = 0; k < bucket.length; k++) {
// 如果桶中有数据,才取出放回原数组
if (bucketElementCounts[k] != 0) {
// 说明桶中有数据,对该桶进行遍历
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放回原数组
arr[index++] = bucket[k][l];
}
}
// 第一轮处理后,需要将每个bucketElementCounts[k]置0
bucketElementCounts[k] = 0;
}
System.out.println("第一轮:" + Arrays.toString(arr));
// ----------------------------
// 第二轮(针对每个元素的十位进行排序处理)
for (int j = 0; j < arr.length; j++) {
// 取出每个元素的十位
int digitOfElement = arr[j] / 10 % 10;
// 将元素放入对应的桶中
// bucketElementCounts[digitOfElement]就是桶中的元素个数,初始为0,放在第一位
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
// 将桶中的元素个数++
// 这样接下来的元素就可以排在前面的元素后面
bucketElementCounts[digitOfElement]++;
}
// 按照桶的顺序取出数据并放回原数组
index = 0;
for (int k = 0; k < bucket.length; k++) {
// 如果桶中有数据,才取出放回原数组
if (bucketElementCounts[k] != 0) {
// 说明桶中有数据,对该桶进行遍历
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放回原数组
arr[index++] = bucket[k][l];
}
}
// 第二轮处理后,需要将每个bucketElementCounts[k]置0
bucketElementCounts[k] = 0;
}
System.out.println("第二轮:" + Arrays.toString(arr));
// ----------------------------
// 第三轮(针对每个元素的百位进行排序处理)
for (int j = 0; j < arr.length; j++) {
// 取出每个元素的百位
int digitOfElement = arr[j] / 100 % 10;
// 将元素放入对应的桶中
// bucketElementCounts[digitOfElement]就是桶中的元素个数,初始为0,放在第一位
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
// 将桶中的元素个数++
// 这样接下来的元素就可以排在前面的元素后面
bucketElementCounts[digitOfElement]++;
}
// 按照桶的顺序取出数据并放回原数组
index = 0;
for (int k = 0; k < bucket.length; k++) {
// 如果桶中有数据,才取出放回原数组
if (bucketElementCounts[k] != 0) {
// 说明桶中有数据,对该桶进行遍历
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放回原数组
arr[index++] = bucket[k][l];
}
}
// 第三轮处理后,需要将每个bucketElementCounts[k]置0
bucketElementCounts[k] = 0;
}
System.out.println("第三轮:" + Arrays.toString(arr));
}
为了方便大家理解,这里我并没有使用循环处理,而是详细写出了每一轮的步骤,代码注释也很详细。
接下来编写测试代码:
public static void main(String[] args) {
int[] arr = { 53, 3, 542, 748, 14, 214 };
raixSort(arr);
}
运行结果:
第一轮:[542, 53, 3, 14, 214, 748]
第二轮:[3, 14, 214, 542, 748, 53]
第三轮:[3, 14, 53, 214, 542, 748]
如果你能够看懂上面的代码,那么接下来就是整合了,通过循环对上面的代码进行优化。
代码如下:
public static void raixSort(int[] arr) {
// 得到数组中最大的数
int max = arr[0];// 假设第一个数就是数组中的最大数
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
// 得到最大数是几位数
// 通过拼接一个空串将其变为字符串进而求得字符串的长度,即为位数
int maxLength = (max + "").length();
// 定义一个二维数组,模拟桶,每个桶就是一个一维数组
// 为了防止放入数据的时候桶溢出,我们应该尽量将桶的容量设置得大一些
int[][] bucket = new int[10][arr.length];
// 记录每个桶中实际存放的元素个数
// 定义一个一维数组来记录每个桶中每次放入的元素个数
int[] bucketElementCounts = new int[10];
// 通过变量n帮助取出元素位数上的数
for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
for (int j = 0; j < arr.length; j++) {
// 针对每个元素的位数进行处理
int digitOfElement = arr[j] / n % 10;
// 将元素放入对应的桶中
// bucketElementCounts[digitOfElement]就是桶中的元素个数,初始为0,放在第一位
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
// 将桶中的元素个数++
// 这样接下来的元素就可以排在前面的元素后面
bucketElementCounts[digitOfElement]++;
}
// 按照桶的顺序取出数据并放回原数组
int index = 0;
for (int k = 0; k < bucket.length; k++) {
// 如果桶中有数据,才取出放回原数组
if (bucketElementCounts[k] != 0) {
// 说明桶中有数据,对该桶进行遍历
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放回原数组
arr[index++] = bucket[k][l];
}
}
// 每轮处理后,需要将每个bucketElementCounts[k]置0
bucketElementCounts[k] = 0;
}
}
}
测试代码:
public static void main(String[] args) {
int[] arr = { 53, 3, 542, 748, 14, 214 };
raixSort(arr);
System.out.println(Arrays.toString(arr));
}
运行结果:
[3, 14, 53, 214, 542, 748]
这样,基数排序就完成了。大家不要看到代码很多就怕了、烦了,觉得好难,其实也不能说一点难度都没有吧,只是要去理解这个过程,所以对于排序过程的分析我写了很多,也是为了能让你们更加理解,掌握了过程之后,相信理解这些代码也不是难事了。
其它:
public static void main(String[] args) {
int[] arr = new int[800000];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * 8000000);
}
Date date = new Date();
SimpleDateFormat format = new SimpleDateFormat("HH:mm:ss");
String dateStr = format.format(date);
System.out.println("排序前的时间是:" + dateStr);
raixSort(arr);
Date date2 = new Date();
String dateStr2 = format.format(date2);
System.out.println("排序前的时间是:" + dateStr2);
}
运行结果:
排序前的时间是:17:37:21
排序前的时间是:17:37:21
一秒钟时间不到就完成排序了。
我们再测试一下八百万个数据的排序:
public static void main(String[] args) {
int[] arr = new int[8000000];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * 8000000);
}
Date date = new Date();
SimpleDateFormat format = new SimpleDateFormat("HH:mm:ss");
String dateStr = format.format(date);
System.out.println("排序前的时间是:" + dateStr);
raixSort(arr);
Date date2 = new Date();
String dateStr2 = format.format(date2);
System.out.println("排序前的时间是:" + dateStr2);
}
运行结果:
排序前的时间是:17:38:04
排序前的时间是:17:38:05
只需要一秒钟即完成了排序。
我们再测试一下八千万个数据的排序:
public static void main(String[] args) {
int[] arr = new int[80000000];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * 8000000);
}
Date date = new Date();
SimpleDateFormat format = new SimpleDateFormat("HH:mm:ss");
String dateStr = format.format(date);
System.out.println("排序前的时间是:" + dateStr);
raixSort(arr);
Date date2 = new Date();
String dateStr2 = format.format(date2);
System.out.println("排序前的时间是:" + dateStr2);
}
运行结果:
排序前的时间是:17:41:07
Exception in thread "main" java.lang.OutOfMemoryError: Java heap space
at com.itcast.sort.RadixSortDemo.raixSort(RadixSortDemo.java:42)
at com.itcast.sort.RadixSortDemo.main(RadixSortDemo.java:22)
结果为堆内存溢出,所以在对大量数据进行排序的时候,基数排序显然不是一个好的选择,因为提升排序效率的条件是牺牲大量的内存空间,当数据足够多时,内存空间就不够用了。
4.堆排序
本来这篇文章打算介绍四种排序算法,这最后一种便是堆排序,但是写着写着,回过头发现竟然也写了这么多了,考虑到不宜篇幅过长,我打算将堆排序放到后面说,如果你能掌握前面的这七种排序算法并能随时手写出来,也是很了不起了。
本篇文章虽然只介绍了三种排序算法,但这三种排序算法都有一定的难度,想要彻底掌握它们大家还是要多花点心思啊!
推荐阅读
程序员那些必须掌握的排序算法——上半部分