BP神经网络简单python实现

#BP神经网络简单python实现

BP神经网络的算法推导详见前面的文章：BP神经网络算法推导

##样例示意图

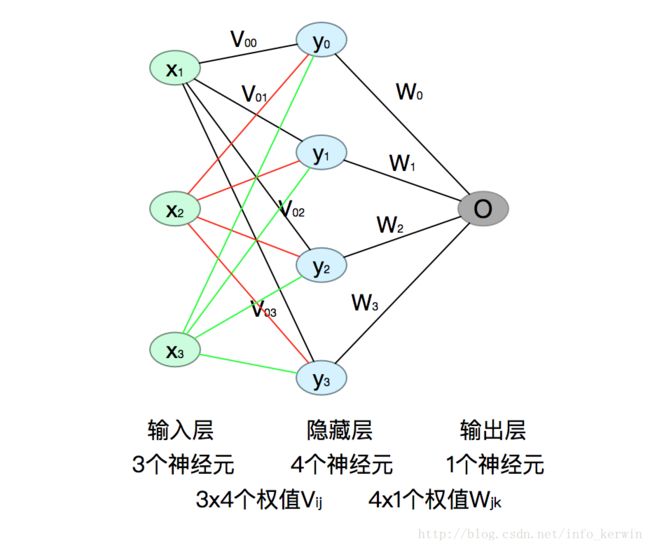
假设输入层有3个神经元，隐藏层有4个神经元，输出层有1个神经元，如图所示：

##样例参数说明

如图所示，隐藏层的结果（输出）为$Y=X\times V_{ij}$：

$$\{\begin{array}{r}{y}_0=x_0{V}_{00}+x_1{V}_{10}+x_2{V}_{20}\\ y_1=x_0{V}_{01}+x_1{V}_{11}+x_2{V}_{21}\\ y_2=x_0{V}_{02}+x_1{V}_{12}+x_2{V}_{22}\\ y_3=x_0{V}_{03}+x_1{V}_{13}+x_2{V}_{23}\end{array}$$

以向量形式表示出来：

$$(y_0{y}_1{y}_2{y}_3{)}_{4\times 4}=(x_0{x}_1{x}_2{)}_{4\times 3}{\left(\begin{array}{cccc}{V}_{00}& V_{01}& V_{02}& V_{03}\\ V_{10}& V_{11}& V_{12}& V_{13}\\ V_{20}& V_{21}& V_{22}& V_{23}\end{array}\right)}_{3\times 4}$$

输出层的结果为$O=Y\times W_{jk}$：

$$O_{4\times 1}=(y_0{y}_1{y}_2{y}_3{)}_{4\times 4}\times {\left(\begin{array}{c}{W}_0\\ W_1\\ W_2\\ W_3\end{array}\right)}_{4\times 1}$$

因为本例子使用3层BP神经网络解决异或问题，则输入为00，01，10，11，期望得到的输出为0，1，1，0，如下所示：

$$\left(\begin{array}{cccc}{X}_0& X_1& X_2& d_{esire}\\ 1& 0& 0& 0\\ 1& 0& 1& 1\\ 1& 1& 0& 1\\ 1& 1& 1& 0\end{array}\right)$$

##代码实现

#导入numpy包（用python实现的科学计算包）
import numpy as np
#输入数据X,异或问题的输入00，01，10，11，加上X0，组成4x3的输入矩阵
X = np.array([[1,0,0],
              [1,0,1],
              [1,1,0],
              [1,1,1]])
#期望输出Desire，根据输入对应的期望输出为0，1，1，0
D = np.array([[0,1,1,0]])
#权值初始化，取值范围-1到1
V = np.random.random((3,4))*2-1 
W = np.random.random((4,1))*2-1
#打印权值V的初始值
print(V)
#打印权值W的初始值
print(W)
#学习率Learning Rate设置，学习率太大迭代次数少了，但是不够准确，学习率太小会导致迭代次数过高还无法得到较好结果，这里将学习率设置为0.11
lr = 0.11

#定义sigmoid转移函数，取值范围为（0，1）
def sigmoid(x):
    return 1/(1+np.exp(-x))
#定义sigmoid函数的导数
def dsigmoid(x):
    return x*(1-x)

#定义权值更新函数
def update():
    global X,D,V,W,lr #X为输入，D为期望输出，V为输入层到隐藏层的权值，W为隐藏层到输出层的权值，lr为学习率
    
    Y = sigmoid(np.dot(X,V))#隐藏层输出(4x4)
    O = sigmoid(np.dot(Y,W))#输出层实际输出(4x1)
    
    #误差信号O_delta及Y_delta
    O_delta = (D.T - O)*dsigmoid(O)
    Y_delta = O_delta.dot(W.T)*dsigmoid(Y)
    
    #权值的改变值
    W_C = lr*Y.T.dot(O_delta)
    V_C = lr*X.T.dot(Y_delta)
    
    #更新权值
    W = W + W_C
    V = V + V_C

#迭代20000次，进行权值更新，每个500次打印一下误差，观察误差的变化过程，误差求法为理想输出-实际输出，求绝对值后取均值。
for i in range(20000):
    update()#更新权值
    if i%500==0:
        Y = sigmoid(np.dot(X,V))#隐藏层输出(4,4)
        O = sigmoid(np.dot(Y,W))#输出层输出(4,1)
        print('Error:',np.mean(np.abs(D.T-O)))
        
#打印最终输出值Output
Y = sigmoid(np.dot(X,V))#隐藏层输出(4,4)
O = sigmoid(np.dot(Y,W))#输出层输出(4,1)
print(O)

#定义一个函数，将最终的输出用0和1来表示
def judge(x):
    if x>=0.5:
        return 1
    else:
        return 0
#利用map函数将输出O传入judge函数中
for i in map(judge,O):
    print(i)

---

欢迎访问我的个人简介
http://www.wyfshu.xyz

---

Email:[email protected]
2018-01-16