第二章 感知机的python实现

这里是我的个人网站：
https://endlesslethe.com/perceptron-with-python.html
有更多总结分享，最新更新也只会发布在我的个人网站上。排版也可能会更好看一点=v=

前言

本来想写一个关于感知机的总结，但如果要深入探讨，涉及的东西实在太多。仅仅浅尝辄止的话，那我就相当于照搬原文，违背了我写文章的初衷。

所以就单纯地把我自己写的感知机实现代码发上来，辅助大家学习。
我还提供了一个数据生成器，可以生成训练模型所需要的数据。

简单地对结果做了可视化，具体绘制代码见文末提供的github地址。跪求star=v=

感知机模型

感知机算法用于计算得到划分可二分数据集的超平面S。

我们定义优化函数为损失函数：
L=误分类点到超平面S的距离和

\(d = \frac{1}{{\left| w \right|}}|w \bullet {x_i} + b|\)

\(L = - \sum\limits_N {{y_i}} (w \bullet {x_i} + b)\)

采用随机梯度下降算法

\(\frac{{dL}}{{dw}} = - \sum\limits_N {{y_i}} {x_i}\)

故对于每一个误分类点

\(w = w + \eta {y_i}{x_i}\)

算法流程

输入：w, b；
训练：f(x)=sign(wx+b)

1. 选取初值w0, b0
2. 随机选取数据(xi, yi)
3. 如果为误分类点，则更新

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(1)

def sign(x):
    if x > 0:
        return 1;
    return -1

def svg(x, y, w, b, learning_rate):
    i = np.random.randint(0, x.shape[0])
#     print("svg")
#     print(w.shape)
#     print(x[0].shape)
#     print(np.dot(w, x[i]))
    if y[i] * (np.dot(w, x[i]) + b) <= 0:
        w = w + learning_rate * x[i].T * y[i]
        b = b + learning_rate * y[i]
    params = {'w':w, 'b':b}
    return params

预测

输入：x
输出：y=sign(wx+b)

def predict(x, w, b):
    return sign(np.dot(w, x) + b)

小数据训练

dim = 2 #属性数量
dataSize = 10 #数据集大小
learning_rate = 0.1 #学习率
ITERATE = 1000 #迭代次数

x_train = np.array([[-1, 1], [-2, 0], [-1, 0], [-0.5, 0.5], [0, 0.5],[1, 3], [2, 3], [1, 1], [1, -0.5], [1, 0]])
x_train = x_train.reshape(10, dim, 1)
y_train = np.array([1, 1, 1, 1, 1, -1, -1, -1, -1, -1])
# print(x_train.shape)
# print(x_train[0].shape)

w = np.zeros((1, dim))
b = 0

assert(x_train.shape == (dataSize, dim, 1))
assert(x_train[0].shape == (dim, 1))
assert(w.shape == (1, dim))

for x in range(ITERATE):
    params = svg(x_train, y_train, w, b, learning_rate)
    w = params['w']
    b = params['b']

print(w)
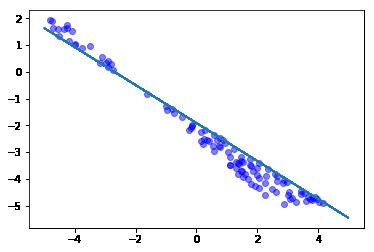
print(b)

训练结果

数据生成器

def getData(rg, dim, size):
#     w = np.random.rand(1, dim)
#     b = np.random.randint(-rg/2, rg/2)
    w = np.array([1, 1])
    b = 2.5
    x = []
    y = []
    for i in range(size):
        x_i = np.random.rand(dim, 1) * rg - rg/2
        y_i = -1
        if np.dot(w, x_i) + b > 0:
            y_i = 1
        x.append(x_i)
        y.append(y_i)
    x = np.array(x)
    y = np.array(y)
#     print("getData")
#     print(x)
    data = {"x":x, "y":y}
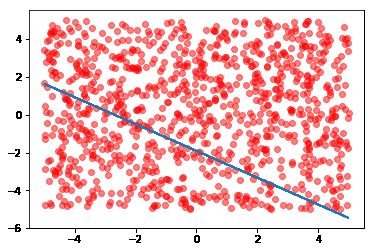
    return data

大数据测试

rangeOfNumber = 10 #随机数的范围
dim = 2 #属性数量
dataSize = 1000 #数据集大小
testSize = 2000 #测试集大小
learning_rate = 0.05 #学习率
ITERATE = 1000 #迭代次数

data_train = getData(rangeOfNumber, dim, dataSize)
x_train = data_train["x"]
y_train = data_train["y"]
# print(x_train.shape)
# print(x_train[0].shape)

w = np.zeros((1, dim))
b = 0

assert(x_train.shape == (dataSize, dim, 1))
assert(x_train[0].shape == (dim, 1))
assert(w.shape == (1, dim))

for x in range(ITERATE):
    params = svg(x_train, y_train, w, b, learning_rate)
    w = params['w']
    b = params['b']

print(w)
print(b)

训练结果

对测试集预测

data_test = getData(rangeOfNumber, dim, testSize)
x_test = data_test["x"]
y_test = data_test["y"]
y_predict = []
for i in range(testSize):
    y_predict.append(predict(x_test[i], w, b))
cnt = 0
for i in range(testSize):
    if y_test[i] == y_predict[i]:
        cnt = cnt + 1
print("Accuracy:%d"  % (cnt / testSize * 100))

误分类样本分布

完整代码

戳我的github