PyTorch 学习笔记（六）：PyTorch的十七个损失函数

本文截取自《PyTorch 模型训练实用教程》，获取全文pdf请点击：https://github.com/tensor-yu/PyTorch_Tutorial

我们所说的优化，即优化网络权值使得损失函数值变小。但是，损失函数值变小是否能代表模型的分类/回归精度变高呢？那么多种损失函数，应该如何选择呢？请来了解PyTorch中给出的十七种损失函数吧。

请运行配套代码，代码中有详细解释，有手动计算，这些都有助于理解损失函数原理。
本小节配套代码： /Code/3_optimizer/3_1_lossFunction

1.L1loss

class torch.nn.L1Loss(size_average=None, reduce=None)
官方文档中仍有reduction='elementwise_mean’参数，但代码实现中已经删除该参数
功能：
计算output和target之差的绝对值，可选返回同维度的tensor或者是一个标量。
计算公式：

参数：
reduce(bool)- 返回值是否为标量，默认为True
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
实例：
/Code/3_optimizer/3_1_lossFunction/1_L1Loss.py

2.MSELoss

class torch.nn.MSELoss(size_average=None, reduce=None, reduction=‘elementwise_mean’)
官方文档中仍有reduction='elementwise_mean’参数，但代码实现中已经删除该参数
功能：
计算output和target之差的平方，可选返回同维度的tensor或者是一个标量。
计算公式：

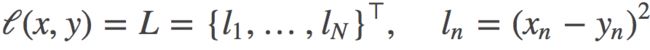
参数：
reduce(bool)- 返回值是否为标量，默认为True
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
实例：
/Code/3_optimizer/3_1_lossFunction/2_MSELoss.py

3.CrossEntropyLoss

class torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction=‘elementwise_mean’)
功能：
将输入经过softmax激活函数之后，再计算其与target的交叉熵损失。即该方法将nn.LogSoftmax()和 nn.NLLLoss()进行了结合。严格意义上的交叉熵损失函数应该是nn.NLLLoss()。

补充：小谈交叉熵损失函数
交叉熵损失(cross-entropy Loss) 又称为对数似然损失(Log-likelihood Loss)、对数损失；二分类时还可称之为逻辑斯谛回归损失(Logistic Loss)。交叉熵损失函数表达式为 L = - sigama(y_i * log(x_i))。pytroch这里不是严格意义上的交叉熵损失函数，而是先将input经过softmax激活函数，将向量“归一化”成概率形式，然后再与target计算严格意义上交叉熵损失。
在多分类任务中，经常采用softmax激活函数+交叉熵损失函数，因为交叉熵描述了两个概率分布的差异，然而神经网络输出的是向量，并不是概率分布的形式。所以需要softmax激活函数将一个向量进行“归一化”成概率分布的形式，再采用交叉熵损失函数计算loss。
再回顾PyTorch的CrossEntropyLoss()，官方文档中提到时将nn.LogSoftmax()和 nn.NLLLoss()进行了结合，nn.LogSoftmax() 相当于激活函数 ， nn.NLLLoss()是损失函数，将其结合，完整的是否可以叫做softmax+交叉熵损失函数呢？

计算公式：

参数：
weight(Tensor)- 为每个类别的loss设置权值，常用于类别不均衡问题。weight必须是float类型的tensor，其长度要于类别C一致，即每一个类别都要设置有weight。带weight的计算公式：

size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True
ignore_index(int)- 忽略某一类别，不计算其loss，其loss会为0，并且，在采用size_average时，不会计算那一类的loss，除的时候的分母也不会统计那一类的样本。
实例：
/Code/3_optimizer/3_1_lossFunction/3_CroosEntropyLoss.py
补充：
output不仅可以是向量，还可以是图片，即对图像进行像素点的分类，这个例子可以从NLLLoss()中看到，这在图像分割当中很有用。

4.NLLLoss

class torch.nn.NLLLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction=‘elementwise_mean’)
功能：
不好用言语描述其功能！请看计算公式：loss(input, class) = -input[class]。举个例，三分类任务，input=[-1.233, 2.657, 0.534]， 真实标签为2（class=2），则loss为-0.534。就是对应类别上的输出，取一个负号！感觉被NLLLoss的名字欺骗了。
实际应用：
常用于多分类任务，但是input在输入NLLLoss()之前，需要对input进行log_softmax函数激活，即将input转换成概率分布的形式，并且取对数。其实这些步骤在CrossEntropyLoss中就有，如果不想让网络的最后一层是log_softmax层的话，就可以采用CrossEntropyLoss完全代替此函数。
参数：
weight(Tensor)- 为每个类别的loss设置权值，常用于类别不均衡问题。weight必须是float类型的tensor，其长度要于类别C一致，即每一个类别都要设置有weight。
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为除以权重之和的平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。
ignore_index(int)- 忽略某一类别，不计算其loss，其loss会为0，并且，在采用size_average时，不会计算那一类的loss，除的时候的分母也不会统计那一类的样本。
实例：
/Code/3_optimizer/3_1_lossFunction/4_NLLLoss.py
特别注意：
当带上权值，reduce = True, size_average = True, 其计算公式为：

例如当input为[[0.6, 0.2, 0.2], [0.4, 1.2, 0.4]]，target= [0, 1], weight = [0.6, 0.2, 0.2]
l1 = - 0.60.6 = - 0.36
l2 = - 1.20.2 = - 0.24
loss = -0.36/(0.6+0.2) + -0.24/(0.6+0.2) = -0.75

5.PoissonNLLLoss

class torch.nn.PoissonNLLLoss(log_input=True, full=False, size_average=None, eps=1e-08, reduce=None, reduction=‘elementwise_mean’)
功能：
用于target服从泊松分布的分类任务。
计算公式：

参数：
log_input(bool)- 为True时，计算公式为：loss(input,target)=exp(input) - target * input;
为False时，loss(input,target)=input - target * log(input+eps)
full(bool)- 是否计算全部的loss。例如，当采用斯特林公式近似阶乘项时，此为 target*log(target) - target+0.5∗log(2πtarget)
eps(float)- 当log_input = False时，用来防止计算log(0)，而增加的一个修正项。即 loss(input,target)=input - target * log(input+eps)
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True
实例：
/Code/3_optimizer/3_1_lossFunction/5_PoissonNLLLoss.py

6.KLDivLoss

class torch.nn.KLDivLoss(size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
计算input和target之间的KL散度( Kullback–Leibler divergence) 。
计算公式：

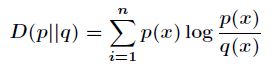
（后面有代码手动计算，证明计算公式确实是这个，但是为什么没有对x_n计算对数呢？）

补充：KL散度
KL散度( Kullback–Leibler divergence) 又称为相对熵(Relative Entropy)，用于描述两个概率分布之间的差异。计算公式(离散时)：

其中p表示真实分布，q表示p的拟合分布， D(P||Q)表示当用概率分布q来拟合真实分布p时，产生的信息损耗。这里的信息损耗，可以理解为损失，损失越低，拟合分布q越接近真实分布p。同时也可以从另外一个角度上观察这个公式，即计算的是 p 与 q 之间的对数差在 p 上的期望值。
特别注意，D(p||q) ≠ D(q||p)， 其不具有对称性，因此不能称为K-L距离。
信息熵 = 交叉熵 - 相对熵
从信息论角度观察三者，其关系为信息熵 = 交叉熵 - 相对熵。在机器学习中，当训练数据固定，最小化相对熵 D(p||q) 等价于最小化交叉熵 H(p,q) 。

参数：
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值，平均值为element-wise的，而不是针对样本的平均；为False时，返回是各样本各维度的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。

使用注意事项：
要想获得真正的KL散度，需要如下操作：

1. reduce = True ；size_average=False
2. 计算得到的loss 要对batch进行求平均

实例：
/Code/3_optimizer/3_1_lossFunction/6_KLDivLoss.py

7.BCELoss

class torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
二分类任务时的交叉熵计算函数。此函数可以认为是nn.CrossEntropyLoss函数的特例。其分类限定为二分类，y必须是{0,1}。还需要注意的是，input应该为概率分布的形式，这样才符合交叉熵的应用。所以在BCELoss之前，input一般为sigmoid激活层的输出，官方例子也是这样给的。该损失函数在自编码器中常用。
计算公式：

参数：
weight(Tensor)- 为每个类别的loss设置权值，常用于类别不均衡问题。
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True

8.BCEWithLogitsLoss

class torch.nn.BCEWithLogitsLoss(weight=None, size_average=None, reduce=None, reduction=‘elementwise_mean’, pos_weight=None)
功能：
将Sigmoid与BCELoss结合，类似于CrossEntropyLoss(将nn.LogSoftmax()和 nn.NLLLoss()进行结合）。即input会经过Sigmoid激活函数，将input变成概率分布的形式。
计算公式：

σ() 表示Sigmoid函数
特别地，当设置weight时：

参数：
weight(Tensor)- : 为batch中单个样本设置权值，If given, has to be a Tensor of size “nbatch”.
pos_weight-: 正样本的权重, 当p>1，提高召回率，当P<1，提高精确度。可达到权衡召回率(Recall)和精确度(Precision)的作用。 Must be a vector with length equal to the number of classes.
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True

9.MarginRankingLoss

class torch.nn.MarginRankingLoss(margin=0, size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
计算两个向量之间的相似度，当两个向量之间的距离大于margin，则loss为正，小于margin，loss为0。
计算公式：

y == 1时，x1要比x2大，才不会有loss，反之，y == -1 时，x1要比x2小，才不会有loss。
参数：
margin(float)- x1和x2之间的差异。
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。

10.HingeEmbeddingLoss

class torch.nn.HingeEmbeddingLoss(margin=1.0, size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
未知。为折页损失的拓展，主要用于衡量两个输入是否相似。 used for learning nonlinear embeddings or semi-supervised 。
计算公式：

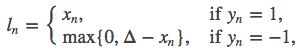
参数：
margin(float)- 默认值为1，容忍的差距。
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。

11.MultiLabelMarginLoss

class torch.nn.MultiLabelMarginLoss(size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
用于一个样本属于多个类别时的分类任务。例如一个四分类任务，样本x属于第0类，第1类，不属于第2类，第3类。
计算公式：

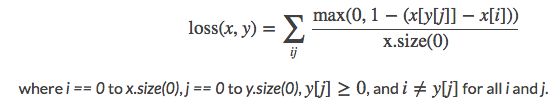
x[y[j]] 表示 样本x所属类的输出值，x[i]表示不等于该类的输出值。

参数：
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。
Input: © or (N,C) where N is the batch size and C is the number of classes.
Target: © or (N,C), same shape as the input.

12.SmoothL1Loss

class torch.nn.SmoothL1Loss(size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
计算平滑L1损失，属于 Huber Loss中的一种(因为参数δ固定为1了)。
补充：
Huber Loss常用于回归问题，其最大的特点是对离群点（outliers）、噪声不敏感，具有较强的鲁棒性。
公式为：

理解为，当误差绝对值小于δ，采用L2损失；若大于δ，采用L1损失。
回到SmoothL1Loss，这是δ=1时的Huber Loss。
计算公式为：

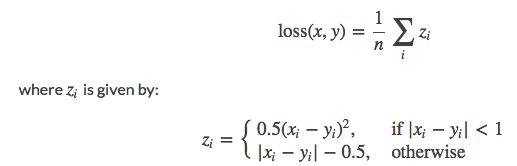
对应下图红色线：

参数：
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。

13.SoftMarginLoss

class torch.nn.SoftMarginLoss(size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
Creates a criterion that optimizes a two-class classification logistic loss between input tensor xand target tensor y (containing 1 or -1). （暂时看不懂怎么用，有了解的朋友欢迎补充！）
计算公式：

参数：
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。

14.MultiLabelSoftMarginLoss

class torch.nn.MultiLabelSoftMarginLoss(weight=None, size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
SoftMarginLoss多标签版本，a multi-label one-versus-all loss based on max-entropy,
计算公式：

参数：
weight(Tensor)- 为每个类别的loss设置权值。weight必须是float类型的tensor，其长度要于类别C一致，即每一个类别都要设置有weight。

15.CosineEmbeddingLoss

class torch.nn.CosineEmbeddingLoss(margin=0, size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
用Cosine函数来衡量两个输入是否相似。 used for learning nonlinear embeddings or semi-supervised 。
计算公式：

参数：
margin(float)- ： 取值范围[-1,1]， 推荐设置范围 [0, 0.5]
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。

16.MultiMarginLoss

class torch.nn.MultiMarginLoss(p=1, margin=1, weight=None, size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
计算多分类的折页损失。
计算公式：

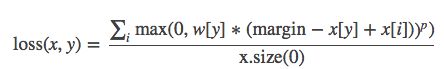
其中，0≤y≤x.size(1) ; i == 0 to x.size(0) and i≠y; p==1 or p ==2; w[y]为各类别的weight。
参数：
p(int)- 默认值为1，仅可选1或者2。
margin(float)- 默认值为1
weight(Tensor)- 为每个类别的loss设置权值。weight必须是float类型的tensor，其长度要于类别C一致，即每一个类别都要设置有weight。
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。

17.TripletMarginLoss

class torch.nn.TripletMarginLoss(margin=1.0, p=2, eps=1e-06, swap=False, size_average=None, reduce=None, reduction=‘elementwise_mean’)
功能：
计算三元组损失，人脸验证中常用。
如下图Anchor、Negative、Positive，目标是让Positive元和Anchor元之间的距离尽可能的小，Positive元和Negative元之间的距离尽可能的大。

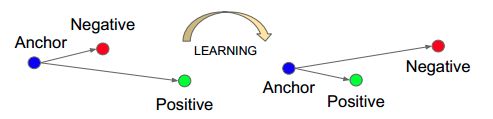
从公式上看，Anchor元和Positive元之间的距离加上一个threshold之后，要小于Anchor元与Negative元之间的距离。

计算公式：

参数：
margin(float)- 默认值为1
p(int)- The norm degree ，默认值为2
swap(float)– The distance swap is described in detail in the paper Learning shallow convolutional feature descriptors with triplet losses by V. Balntas, E. Riba et al. Default: False
size_average(bool)- 当reduce=True时有效。为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
reduce(bool)- 返回值是否为标量，默认为True。

---

转载请注明出处：https://blog.csdn.net/u011995719/article/details/85107524