《人工智能》机器学习 - 第6章感知机模型(一 理论讲解)
6.1引言
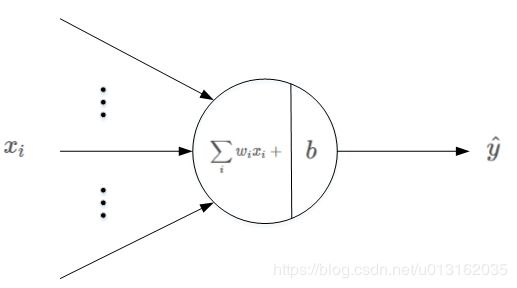
PLA全称是Perceptron Linear Algorithm,即线性感知机算法,属于一种最简单的感知机(Perceptron)模型。感知机(perceptron)是二分类的线性分类模型,它的基本结构如图1所示,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面,属于判别模型,解决的问题是分类问题。感知机学习算法具有简单而易于实现的优点,分为原始形式和对偶形式。感知机预测是用学习得到的感知机模型对新的输入实例进行分类。感知机算法是1957年由Rosenblatt提出的,是支持向量机(SVM)和神经网络的基础,学好感知机对SVM和神经网络大有裨益。
其中, x i x_i xi是输入, w i w_i wi 表示权重系数, b b b表示偏移常数。
依照统计学习三要素来说:
- 模型:符号函数(判别模型);
- 策略:损失函数:误分点到超平面距离之和;
- 算法:利用梯度下降算法进行优化。
好了,开始学习感知机算法吧,本章的目标(目的)是,求出将训练数据进行线性划分的分类超平面,为此导入误分类的损失函数,利用梯度下降法对损失函数进行最小化,求的感知机模型。
6.2感知机模型
6.2.1感知机模型定义
假设输入空间(特征空间)是 χ ⊆ R n \chi\subseteq R^n χ⊆Rn,输出空间是 Y = + 1 , − 1 Y={+1,-1} Y=+1,−1 。输入 x ⊆ χ x \subseteq\chi x⊆χ表示实例的特征向量,对应于输入空间(特征空间)的点;输出 y ⊆ Y y\subseteq Y y⊆Y表示实例的类别。由输入空间到输出空间的如下函数:
f ( x ) = s i g n ( w ⋅ x + b ) \color{red}f(x)=sign(w\cdot x+b) f(x)=sign(w⋅x+b)
称为感知机。其中,其中, w w w和 b b b为感知机的模型参数, w ⊆ R n w\subseteq R^n w⊆Rn叫作权值(weight)或权值向量(weight vector), b ⊆ R b\subseteq R b⊆R叫做偏置(bias), w ⋅ x w\cdot x w⋅x表示 w w w和 x x x的内积, s i g n ( ) sign() sign()是符号函数:
s i g n ( x ) = { + 1 x ≤ 0 − 1 x < 0 sign(x)= \begin{cases} +1& {x\leq0}\\ -1& {x<0} \end{cases} sign(x)={+1−1x≤0x<0
感知机是一种线性分类模型,属于判别模型。感知机模型的假设空间是定义在特征空间中的所有线性分类模型或者线性分类器,即函数集合:
{ f ∣ f ( x ) = w ⋅ x + b } \{f|f(x)=w\cdot x+b\} {f∣f(x)=w⋅x+b}
6.2.2感知机模型几何解释
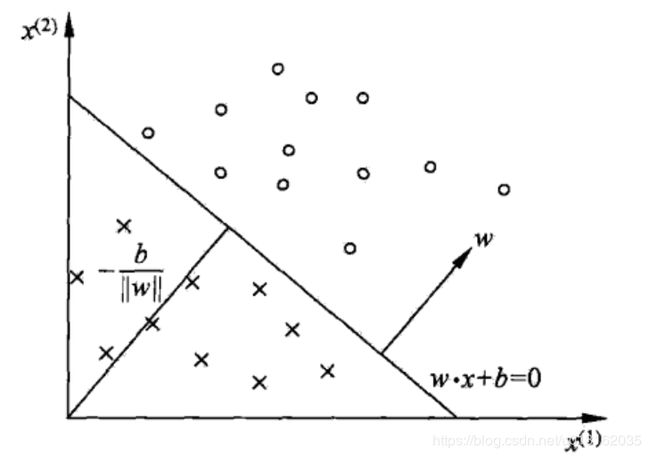
线性方程 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0对应于特征空间 R n R^n Rn中的一个超平面 S S S,其中 w w w是超平面的法向量, b b b是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部分的点(特征向量)被分为正负两类,因为超平面 S S S称为分类超平面(separating hyperplane)。
【注1】超平面
在 R n R^n Rn空间中的超平面为:
w ⃗ ⋅ x ⃗ + b = 0 \vec{w}\cdot \vec{x}+b=0 w⋅x+b=0
在几维空间中,向量 w ⃗ , x ⃗ \vec{w},\vec{x} w,x就是几维的。当然, w ⃗ , x ⃗ \vec{w},\vec{x} w,x属于该空间。在二维空间下,该方程表示一条直线,直线是平面的超平面。三维空间下,该方程表示一个平面,平面是空间的超平面。
【注2】点到超平面的距离
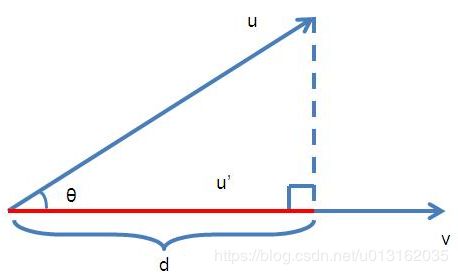
向量的投影:给定两个向量 u ⃗ , v ⃗ \vec{u},\vec{v} u,v ,求 w ⃗ \vec{w} w在 x ⃗ \vec{x} x上的投影长度,向量间的夹角为 c o s θ cosθ cosθ。
d = ∣ u ⃗ ∣ c o s θ d=|\vec{u}|cos\theta d=∣u∣cosθ, c o s θ = u ⃗ ⋅ v ⃗ ∣ u ⃗ ∣ ∣ v ⃗ ∣ cos\theta=\frac{\vec{u}\cdot\vec{v}}{|\vec{u}||\vec{v}|} cosθ=∣u∣∣v∣u⋅v ,综上, d = u ⃗ ⋅ v ⃗ ∣ v ⃗ ∣ d=\frac{\vec{u}\cdot\vec{v}}{|\vec{v}|} d=∣v∣u⋅v .
点到超平面的距离:假设 x 0 x_0 x0是超平面 w ⃗ ⋅ x ⃗ + b = 0 \vec{w}\cdot \vec{x}+b=0 w⋅x+b=0上任意一点,则点 x x x到超平面的距离为 x − x 0 x-x_0 x−x0在超平面法向量 w ⃗ \vec{w} w上的投影长度:
d = ∣ ∣ w ( x − x 0 ) + b ∣ ∣ ∣ ∣ w ∣ ∣ = ∣ ∣ w x − w x 0 + b ∣ ∣ ∣ ∣ w ∣ ∣ = ∣ ∣ w x ⃗ + b ∣ ∣ ∣ ∣ w ∣ ∣ d=\frac{||w(x-x_0)+b||}{||w||}=\frac{||wx-wx_0+b||}{||w||}=\frac{||w\vec{x}+b||}{||w||} d=∣∣w∣∣∣∣w(x−x0)+b∣∣=∣∣w∣∣∣∣wx−wx0+b∣∣=∣∣w∣∣∣∣wx+b∣∣
则原点到超平面的距离 − b ∣ ∣ w ∣ ∣ -\frac{b}{||w||} −∣∣w∣∣b为 。
感知机的学习:由训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)\} T={(x1,y1),(x2,y2),...(xN,yN)}(实例的特征向量以及类别),其中, x i ∈ χ ⊆ R n x_i\in \chi \subseteq R^n xi∈χ⊆Rn, y i ∈ Y ⊆ = { + 1 , − 1 } y_i\in Y \subseteq =\{+1,-1\} yi∈Y⊆={+1,−1} , i = 1 , 2 , 3 , . . . , N i=1,2,3,...,N i=1,2,3,...,N ,求得感知机模型,也就是求出参数 w w w和 b b b。
感知机的预测:通过学习得到的感知机模型,对于新的输入实例给出其对应的输出类别。
6.3感知机策略
给定一个数据集, T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)\} T={(x1,y1),(x2,y2),...(xN,yN)}, x i ∈ χ ⊆ R n x_i\in \chi \subseteq R^n xi∈χ⊆Rn, y i ∈ Y ⊆ = { + 1 , − 1 } y_i\in Y \subseteq =\{+1,-1\} yi∈Y⊆={+1,−1} , i = 1 , 2 , 3 , . . . , N i=1,2,3,...,N i=1,2,3,...,N 。如果存在某个超平面:
w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0
能够将数据集的正实例和负实例完全正确地划分到超平面的两侧,即对所有 y i = ± 1 y_i=\pm1 yi=±1的实例 i i i,有: w ⋅ x i + b > 0 w\cdot x_i+b>0 w⋅xi+b>0;对所有 y = − 1 y=-1 y=−1的实例 i i i,有 w ⋅ x i + b < 0 w\cdot x_i+b<0 w⋅xi+b<0 ,则称数据集 T T T为线性可分数据集(Linear separable dataset);否则,称数据集 T T T线性不可分。
假设训练数据集是线性可分的,感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面,为了找出这样的超平面,即确定感知机模型的参数 w , b w,b w,b,需要确定一个学习策略,即定义(经验)损失函数并将损失函数最小化。
损失函数的一个自然选择是误分类点的总数,但是这样的损失函数不是参数 w , b w,b w,b的连续可导函数,不宜优化。损失函数的另一个选择是误分类点到超平面 S S S的总距离,这是感知机所采用的。为此,首先,写出输入空间 R n R^n Rn中任意一点 x 0 x_0 x0 ,到超平面 S S S的距离(点到直线的距离):
1 ∣ ∣ w ∣ ∣ ∣ w ⋅ x 0 + b ∣ \frac{1}{||w||}|w\cdot x_0+b| ∣∣w∣∣1∣w⋅x0+b∣
其中 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣是 w w w的 L 2 L_2 L2范数。
其次,对于误分类点 ( x i , y i ) (x_i,y_i) (xi,yi)来说,
− y i ( w ⋅ x i + b ) > 0 -y_i(w\cdot x_i+b)>0 −yi(w⋅xi+b)>0
成立。因为当 w ⋅ x 0 + b > 0 w\cdot x_0+b>0 w⋅x0+b>0时 , y i = − 1 y_i=-1 yi=−1,而当 w ⋅ x i + b < 0 w\cdot x_i+b<0 w⋅xi+b<0时, y i = ± 1 y_i=\pm1 yi=±1 。因此误分点 x i x_i xi到超平面 S S S的距离可以写成如下公式:
− 1 ∣ ∣ w ∣ ∣ y i ( w ⋅ x 0 + b ) -\frac{1}{||w||}y_i(w\cdot x_0+b) −∣∣w∣∣1yi(w⋅x0+b)
这样,假设超平面 S S S的误分类点集合为 M M M,那么所有误分类点到超平面 S S S的总距离为:
− 1 ∣ ∣ w ∣ ∣ ∑ x i ⊆ M y i ( w ⋅ x 0 + b ) -\frac{1}{||w||}\sum_{x_i\subseteq M}y_i(w\cdot x_0+b) −∣∣w∣∣1∑xi⊆Myi(w⋅x0+b)
不考虑 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1,则得到感知机学习的损失函数。
【注】不考虑 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1的原因.
1、 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 恒为正,不影响 − y i ( w ⋅ x i + b ) -y_i(w\cdot x_i+b) −yi(w⋅xi+b)正负的判断,也就是不影响学习算法的中间过程。因为感知机学习算法是误分类驱动的(只有当出现误分类时才去调整模型,或者说损失函数只与误分类点有关),这里需要注意的是,所谓的“误分类驱动”指的是我们只需要判断 − y i ( w ⋅ x i + b ) -y_i(w\cdot x_i+b) −yi(w⋅xi+b)的正负来判断分类的正确与否,而 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1并不影响正负值的判断,所以 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 对感知机学习算法的中间过程可有可无。
2、 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 不影响感知机学习算法的最终结果,因为感知机学习算法最终的终止条件是所有的输入都被正确的分类,即不存在误分类点,则此时的损失函数为0,对应于 − 1 ∣ ∣ w ∣ ∣ y i ( w ⋅ x i + b ) -\frac{1}{||w||}y_i(w\cdot x_i+b) −∣∣w∣∣1yi(w⋅xi+b) ,即分子为0.则可以看出 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 对最终结果也无影响。
综上所述,即使忽略 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 ,也不会对感知机学习算法的执行过程产生任何影响,反而还能简化运算,提高算法执行效率。
给定一个数据集, T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)\} T={(x1,y1),(x2,y2),...(xN,yN)} , x i ∈ χ ⊆ R n x_i\in \chi \subseteq R^n xi∈χ⊆Rn, y i ∈ Y ⊆ = { + 1 , − 1 } y_i\in Y \subseteq =\{+1,-1\} yi∈Y⊆={+1,−1} , i = 1 , 2 , 3 , . . . , N i=1,2,3,...,N i=1,2,3,...,N 。感知机 s i g n ( w ⋅ x + b ) sign(w\cdot x+b) sign(w⋅x+b)学习的损失函数定义为:
L ( w , b ) = − ∑ x i ⊆ M y i ( w ⋅ x i + b ) L(w,b)=-\sum_{x_i\subseteq M}y_i(w\cdot x_i+b) L(w,b)=−∑xi⊆Myi(w⋅xi+b)
其中, M M M为误分类点的集合,这个损失函数就是感知机学习的经验风险函数。
显然,损失函数 L ( w , b ) L(w,b) L(w,b)是非负的。如果没有误分类点,损失函数值就是0。而且误分类点越少,误分类点离超平面越近,都会使得损失函数值越小。一个特定的样本点的损失函数:在误分类时是参数 w , b w,b w,b的线性函数,在正确分类的时候是0,因此,给定训练数据集 T T T,损失函数 L ( w , b ) L(w,b) L(w,b)是 w , b w,b w,b的连续可导函数。
总之,感知机学习的策略是在假设空间中选取使得损失函数式最小的模型参数 w , b w,b w,b,即感知机模型。
6.4感知机学习算法
6.4.1感知机算法的原始形式
给定一个数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)\} T={(x1,y1),(x2,y2),...(xN,yN)} , x i ∈ χ ⊆ R n x_i\in \chi \subseteq R^n xi∈χ⊆Rn, y i ∈ Y ⊆ = { + 1 , − 1 } y_i\in Y \subseteq =\{+1,-1\} yi∈Y⊆={+1,−1} , i = 1 , 2 , 3 , . . . , N i=1,2,3,...,N i=1,2,3,...,N 。求参数 w , b w,b w,b,使其为以下损失函数极小化问题的解:
m i n w , b ( L ( w , b ) ) = − ∑ x i ⊆ M y i ( w ⋅ x i + b ) \underset{w,b}{min}(L(w,b))=-\sum_{x_i\subseteq M}y_i(w\cdot x_i+b) w,bmin(L(w,b))=−∑xi⊆Myi(w⋅xi+b)
其中, M M M为误分类点的集合。
感知机学习算法是误分类驱动的,具体采用随机梯度下降算法。首先,任意选择一个超平面 w 0 , b 0 w_0,b_0 w0,b0 ,然后用梯度下降算法不断极小化目标函数。极小化过程中不是一次使 M M M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。
假设误分类点集合 M M M时固定的,那么损失函数 L ( w , b ) L(w,b) L(w,b)的梯度由:
▽ w L ( w , b ) ) = − ∑ x i ⊂ M y i x i \bigtriangledown_wL(w,b))=-\sum_{x_i\subset M}y_ix_i ▽wL(w,b))=−∑xi⊂Myixi
▽ b L ( w , b ) ) = − ∑ x i ⊂ M y i x i \bigtriangledown_bL(w,b))=-\sum_{x_i\subset M}y_ix_i ▽bL(w,b))=−∑xi⊂Myixi
给出。
随机选取一个误分类点 ( x i , y i ) (x_i,y_i) (xi,yi),对 w , b w,b w,b进行更新:
w ← w + η y i x i w \leftarrow w +\eta y_ix_i w←w+ηyixi
b ← + η y i b\leftarrow+\eta y_i b←+ηyi
其中, η ( 0 < η ≤ 1 ) \eta(0<\eta \leq 1) η(0<η≤1)是步长,在统计学习中又称为学习率(learning rate)。这样,通过迭代,可以期待损失函数 L ( w , b ) L(w,b) L(w,b)不断缩小,直到为0,综上所述,得到如下算法:
算法:感知机算法的原始形式
输入:训练数据集, T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)\} T={(x1,y1),(x2,y2),...(xN,yN)} ,其中, x i ∈ χ ⊆ R n x_i\in \chi \subseteq R^n xi∈χ⊆Rn, y i ∈ Y ⊆ = { + 1 , − 1 } y_i\in Y \subseteq =\{+1,-1\} yi∈Y⊆={+1,−1} , i = 1 , 2 , 3 , . . . , N i=1,2,3,...,N i=1,2,3,...,N ,学习率 η ( 0 < η ≤ 1 ) \eta(0<\eta \leq 1) η(0<η≤1) ;
输出: w , b w,b w,b ;感知机模型 f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w\cdot x+b) f(x)=sign(w⋅x+b) 。
(1)选取初值 w 0 , b 0 w_0,b_0 w0,b0;
(2)在训练集中选取数据 ( x i , y i ) (x_i,y_i) (xi,yi);
(3)如果 y i ( w ⋅ x i + b ) ≤ 0 y_i(w\cdot x_i+b)\leq 0 yi(w⋅xi+b)≤0
w ← w + η y i x i w \leftarrow w +\eta y_ix_i w←w+ηyixi
b ← + η y i b\leftarrow+\eta y_i b←+ηyi
(4)转至(2),直到训练集中没有误分点。
这种学习算法直观上有如下解释,当一个实例点被误分类,即位于分离超平面错误的一侧时,则调整 w , b w,b w,b的值,使分离超平面向该误分类点的一侧移动,以减少误分类点与超平面之间的距离,直到超平面越过该误分类点,使其被正确分类。
感知机学习算法由于采不同的初始值 ( w 0 , b 0 ) (w_0,b_0) (w0,b0)或者选取不同的误分类点(因为在选取误分类点的时候是随机选取的),最终解可以不同。
例1(原始形式求解)
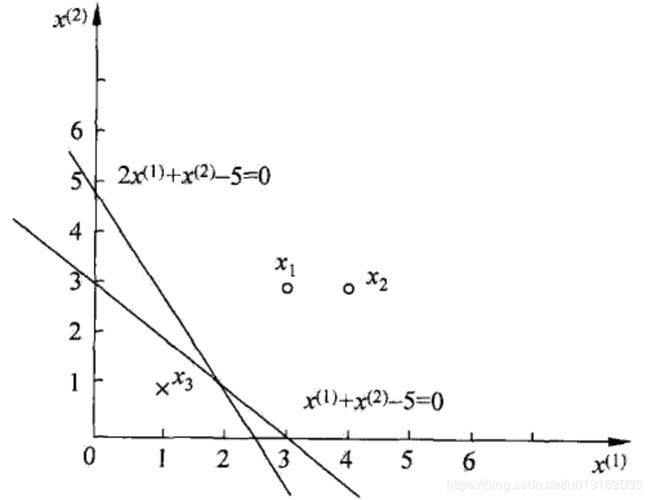
如下图所示的训练集,真正实例点是 x i = ( 3 , 3 ) T x_i=(3,3)^T xi=(3,3)T , x 2 = ( 4 , 3 ) T x_2=(4,3)^T x2=(4,3)T ,负实例点是 x 3 = ( 1 , 1 ) T x_3=(1,1)^T x3=(1,1)T ,试用感知机算法的原始形式求感知机模型 f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w\cdot x+b) f(x)=sign(w⋅x+b) 。这里, w = ( w ( 1 ) , w ( 2 ) ) T w=(w^{(1)},w^{(2)})^T w=(w(1),w(2))T , x = ( x ( 1 ) , x ( 2 ) ) T x=(x^{(1)},x^{(2)})^T x=(x(1),x(2))T 。
解:构建最优问题: m i n w , b ( L ( w , b ) ) = − ∑ x i ⊆ M y i ( w ⋅ x i + b ) \underset{w,b}{min}(L(w,b))=-\sum_{x_i\subseteq M}y_i(w\cdot x_i+b) w,bmin(L(w,b))=−∑xi⊆Myi(w⋅xi+b)
根据上述算法求解得到 w , b , η = 1 w,b,\eta =1 w,b,η=1。
(1)取初值, w 0 = 0 , b 0 = 0 w_0=0,b_0=0 w0=0,b0=0 ;
(2)对 x i = ( 3 , 3 ) T x_i=(3,3)^T xi=(3,3)T , y i ( w 0 ⋅ x i + b 0 ) = 0 y_i(w_0\cdot x_i+b_0)=0 yi(w0⋅xi+b0)=0,未能被正确分类,更新 w , b w,b w,b
w 1 = w 0 + y 1 x 1 = ( 3 , 3 ) T w_1=w_0+y_1x_1=(3,3)^T w1=w0+y1x1=(3,3)T, b 1 = b 0 + y 1 = 1 b_1=b_0+y_1=1 b1=b0+y1=1
得到线性模型
w 1 x + b 1 = 3 x ( 1 ) + 3 x ( 2 ) + 1 w_1x+b_1=3x^{(1)}+3x^{(2)}+1 w1x+b1=3x(1)+3x(2)+1
(3)对 x 1 , x 2 x_1,x_2 x1,x2 ,显然, y i ( w 1 ⋅ x i + b 1 ) > 0 y_i(w_1\cdot x_i+b_1)>0 yi(w1⋅xi+b1)>0 被正确分类,不修改 w , b w,b w,b
对 x 3 = ( 1 , 1 ) T x_3=(1,1)^T x3=(1,1)T, y 3 ( w 1 ⋅ x 3 + b 1 ) < 0 y_3(w_1\cdot x_3+b_1)<0 y3(w1⋅x3+b1)<0 被误分类,更新 w , b w,b w,b
w 2 = w 1 + y 3 x 3 = ( 2 , 2 ) T w_2=w_1+y_3x_3=(2,2)^T w2=w1+y3x3=(2,2)T, b 2 = b 1 + y 3 = 0 b_2=b_1+y_3=0 b2=b1+y3=0
得到线性模型
w 2 x + b 2 = 2 x ( 1 ) + 2 x ( 2 ) w_2x+b_2=2x^{(1)}+2x^{(2)} w2x+b2=2x(1)+2x(2)
如此循环下去,直到
w 7 = ( 1 , 1 ) T w_7=(1,1)^T w7=(1,1)T, b 7 = − 3 b_7=-3 b7=−3
w 7 x + b 7 = x ( 1 ) + x ( 2 ) − 3 w_7x+b_7=x^{(1)}+x^{(2)}-3 w7x+b7=x(1)+x(2)−3
对于所有的分类点,没有误分类点,损失函数最小。
分类超平面为: x ( 1 ) + x ( 2 ) − 3 x^{(1)}+x^{(2)}-3 x(1)+x(2)−3
感知机模型为: f ( x = s i g n ( x ( 1 ) + x ( 2 ) − 3 ) f(x=sign(x^{(1)}+x^{(2)}-3) f(x=sign(x(1)+x(2)−3)
迭代过程表:
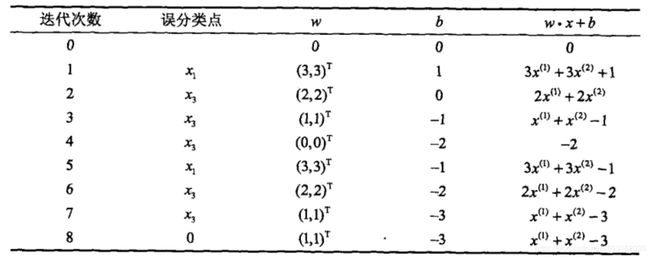
这是在计算中误分点先后取 得到的分离超平面和感知机模型,如果在计算中误分点依次取 ,那么得到的分离超平面是 。可知,感知机模型算法由于采用不同的初值或选取不同的误分类点,解可以不同。
【注】收敛性证明:
《Convergence Proof for the Perceptron Algorithm》
6.4.1感知机算法的对偶形式
对偶形式的基本想法是,将w和b表示为实例 和标记 的线性组合的形式,通过求解其系数而求得 w w w和 b b b。假设设初始值 w 0 , b 0 w_0,b_0 w0,b0均为0,。对误分类点 x i , y i x_i,y_i xi,yi通过
α i ← α i + η y i x i \alpha_i\leftarrow\alpha_i+\eta y_ix_i αi←αi+ηyixi
b ← + η y i b\leftarrow+\eta y_i b←+ηyi
逐步修改 w w w, b b b,设修改 n n n次,则 w , b w,b w,b关于 x i , y i x_i,y_i xi,yi的增量分别是和,这里,这样从学习过程中,不难看出,最后学习得到的 w , b w,b w,b可以分别表示为
∑ i = 1 N α i y i x i \sum_{i=1}^{N}\alpha_iy_ix_i ∑i=1Nαiyixi
b = ∑ i = 1 N α i y i b=\sum_{i=1}^{N}\alpha_i y_i b=∑i=1Nαiyi
其中, α i > = 0 \alpha_i>= 0 αi>=0 , i = 1 , 2 , . . . , N i=1,2,...,N i=1,2,...,N当 η = 1 \eta =1 η=1时,表示第 i i i个实例点由于误分而进行更新的次数,实例点更新的次数越多,意味着它离分离超平面越近,也就越难分类。
算法:感知机算法的对偶形式
输入:训练数据集, T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)\} T={(x1,y1),(x2,y2),...(xN,yN)},其中, x i ∈ χ ⊆ R n x_i\in \chi \subseteq R^n xi∈χ⊆Rn, y i ∈ Y ⊆ = { + 1 , − 1 } y_i\in Y \subseteq =\{+1,-1\} yi∈Y⊆={+1,−1} , i = 1 , 2 , 3 , . . . , N i=1,2,3,...,N i=1,2,3,...,N ,学习率 η ( 0 < η ≤ 1 ) \eta(0<\eta\leq 1) η(0<η≤1);
输出: α , b \alpha,b α,b;感知机模型 f ( x ) = s i g n ( ∑ j = 1 N α j y j x j ⋅ x i + b ) f(x)=sign(\sum_{j=1}^{N}\alpha_jy_jx_j\cdot x_i+b) f(x)=sign(∑j=1Nαjyjxj⋅xi+b)。
(1) a ← 0 , a\leftarrow0, a←0, b ← 0 b\leftarrow0 b←0;
(2)在训练集中选取数据 ( x i , y i ) (x_i,y_i) (xi,yi);
(3)如果 y i ( ∑ j = 1 N α j y j x j ⋅ x i + b ) ≤ 0 y_i(\sum_{j=1}^{N}\alpha_jy_jx_j\cdot x_i+b) \leq0 yi(∑j=1Nαjyjxj⋅xi+b)≤0
α i ← α i + η \alpha_i\leftarrow\alpha_i+\eta αi←αi+η
b ← + η y i b\leftarrow+\eta y_i b←+ηyi
(4)转至(2),直到训练集中没有误分点。
对偶形式中训练实例仅以内积的形式出现,为了方便,可以预先将训练集中实例间的内积计算出来,并以矩阵的形式存储,这个矩阵就是所谓的Gram矩阵:
G = [ x i ⋅ x j ] N × N G=[x_i\cdot x_j]_{N\times N} G=[xi⋅xj]N×N
例2(对偶形式求解)
数据同例1,使用感知机学习算法的对偶形式求解感知机模型。
解:
(1)取 α j = 0 \alpha_j=0 αj=0 i = 1 , 2 , 3 i=1,2,3 i=1,2,3 , b = 0 b=0 b=0, η = 1 \eta=1 η=1
(2)计算Gram矩阵
(3) G = [ 18 21 6 21 25 7 6 7 2 ] G=\left[ \begin{matrix} 18 & 21 & 6 \\ 21 & 25 & 7 \\ 6 & 7 & 2 \end{matrix} \right] \tag{3} G=⎣⎡1821621257672⎦⎤(3)
(3)误分条件
y i ( ∑ j = 1 N α j y j x j ⋅ x i + b ) ≤ 0 y_i(\sum_{j=1}^{N}\alpha_jy_jx_j\cdot x_i+b) \leq0 yi(∑j=1Nαjyjxj⋅xi+b)≤0
参数更新
α i ← α i + 1 , b ← + y i \alpha_i\leftarrow\alpha_i+1,b\leftarrow+y_i αi←αi+1,b←+yi
(4)迭代,对于 x 1 = ( 3 , 3 ) T , y i ( 0 ∗ y i x 1 ⋅ x 1 + b 0 ) = 0 x_1=(3,3)^T,y_i(0 *y_ix_1\cdot x_1+b_0)=0 x1=(3,3)T,yi(0∗yix1⋅x1+b0)=0,未被正确分类,更新 α , b \alpha,b α,b
此时 α 1 = 0 , α 2 = 0 , α 3 = 0 , b = 0 \alpha_1=0,\alpha_2=0,\alpha_3=0,b=0 α1=0,α2=0,α3=0,b=0
α 1 = α 1 + 1 , b = b + 1 , \alpha_1=\alpha_1+1,b=b+1, α1=α1+1,b=b+1,
因此 α 1 = 1 , α 2 = 0 , α 3 = 0 , b = 1 \alpha_1=1,\alpha_2=0,\alpha_3=0,b=1 α1=1,α2=0,α3=0,b=1
y i ( ∑ j = 1 3 α j y j x j ⋅ x i + b ) = ( α 1 y 1 x 1 + α 2 y 2 x 2 + α 3 y 3 x 3 ) x + b = ( α 1 y 1 x 1 ) ⋅ x + b = ( 3 , 3 ) T ⋅ x + 1 y_i(\sum_{j=1}^{3}\alpha_jy_jx_j\cdot x_i+b) =(\alpha_1y_1x_1+\alpha_2y_2x_2+\alpha_3y_3x_3)x+b =(\alpha_1y_1x_1)\cdot x+b =(3,3)^T\cdot x +1 yi(∑j=13αjyjxj⋅xi+b)=(α1y1x1+α2y2x2+α3y3x3)x+b=(α1y1x1)⋅x+b=(3,3)T⋅x+1
如此循环下去,结果如表2.
(5)
w = 2 x 1 + 0 x 2 − 5 x 3 = ( 1 , 1 ) T w=2x_1+0x_2-5x_3=(1,1)^T w=2x1+0x2−5x3=(1,1)T
b = − 3 b=-3 b=−3
分类超平面为:
x ( 1 ) + x ( 2 ) − 3 = 0 x^{(1)}+x^{(2)}-3=0 x(1)+x(2)−3=0
感知机模型为:
f ( x ) = s i g n ( x ( 1 ) + x ( 2 ) − 3 ) f(x)=sign(x^{(1)}+x^{(2)}-3) f(x)=sign(x(1)+x(2)−3)
迭代过程如下:
参考文献:
[1]统计学习方法,李航