《李航：统计学习方法》--- 感知机算法原理与实现

感知机模型

感知机是一个二类分类的线性分类模型。所谓二类分类就是它只能将实例分为正类和负类两个类别。那么为什么是线性分类模型呢，我的理解是感知机学习旨在求出可以将数据进行划分的分离超平面，而分离超平面的方程

w⋅x+b=0

为线性方程，所以感知机为线性分类模型。感知机模型如下图所示：

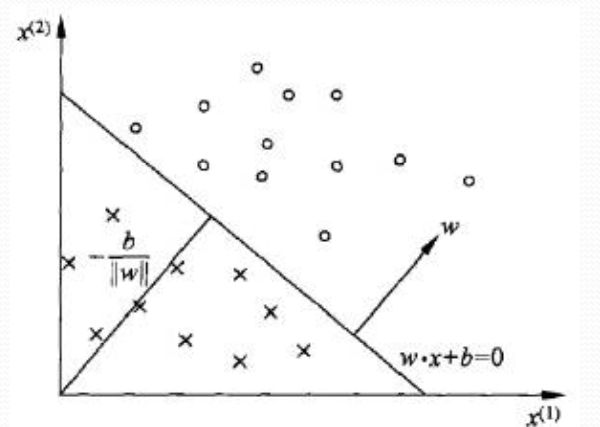
圈圈表示正类，而叉叉表示负类。圈圈与叉叉之间的直线即上文所说的分离超平面（注意分离超平面并不是唯一的！）它将所有的样本划分为两部分。位于分离超平面上方的为正类，记为+1，位于分离超平面下方的为负类，记为-1。也就是说，假设给一个样本的特征向量x，如果 w⋅x+b>0 , 那么样本为正类(+1)，反之若 w⋅x+b<0 , 样本则属于负类(-1)。我们 引入符号函数sign(x)，即

sign(x)={+1，x≥0−1，x<0

由此我们可以得到由输入空间到输出空间的函数

f(x)=sign(w⋅x+b)

这就叫做感知机。其中， w 和 b 为感知机参数， w∈Rn 叫做权值或权值向量， b∈R 叫做偏置， w⋅x 表示 w 和 x 的内积。感知机学习的目的就在于确定参数 w 和 b 的值。

感知机学习策略

给定一个线性可分的数据集

T={(x1,y1),(x2,y2),...(xN,yN)}

其中 xi∈X=Rn ， yi∈Y={+1,−1} ， i=1,2,3,...N 。
为了确定感知机模型的参数 w 和 b ，需要确定一个学习策略，即定义一个损失函数并将损失函数极小化。感知机采用的损失函数为误分类点到超平面的总距离。首先写出输入空间 Rn 中任一点 x0 到分离超平面的距离

1∥w∥|w⋅x0+b|

这里 ∥w∥ 是 w 的 L2 范数。
其次对于误分类的数据 (xi,yi) 来说，

−yi(w⋅xi+b)>0

因为当 w⋅xi+b>0 ， yi=−1 ，而当 w⋅xi+b<0 ， yi=+1 。因此误分类点 xi 到超平面的距离是

−1∥w∥yi(w⋅xi+b)

这样假设误分类点的集合为M，那么所有误分类点到超平面的总距离为

−1∥w∥∑xi∈Myi(w⋅xi+b)

不考虑 1∥w∥ ，就得到感知机学习的损失函数

L(w,b)=−∑xi∈Myi(w⋅xi+b)

显然，损失函数 L(w,b) 是非负的。如果没有误分类点，损失函数值为0，而且，误分类点越少，误分类点离超平面越近，损失函数的值越小。
感知机学习的策略是在假设空间中选取使损失函数最小的模型参数 w,b 。

感知机学习算法

感知机学习算法是误分类驱动的，具体采用随机梯度下降法。首先，任意选取一个超平面 w0,b0 ，然后用梯度下降法不断地极小化损失函数。极小化过程中不是一次使M中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。损失函数 L(w,b) 的梯度为

∇wL(w,b)=−∑xi∈Myixi

∇bL(w,b)=−∑xi∈Myi

随机选取一个误分类点 (xi,yi) ，对 w,b 进行更新：

w←w+ηyixi

b←b+ηyi

式中 η(0<η≤1) 是步长，在统计学习中又称为学习率。

综上所述，得到如下算法(感知机学习算法的原始形式)
输入：训练集 T={(x1,y1),(x2,y2),...(xN,yN)} ，其中 xi∈X=Rn ， yi∈Y={+1,−1} ， i=1,2,3,...N ；学习率 η(0<η≤1) ；
输出： w，b ；感知机模型 f(x)=sign(w⋅x+b)
(1)选取初值 w0，b0
(2)在训练集中选取数据 (xi,yi)
(3)如果 yi(w⋅xi+b)≤0

w←w+ηyixi

b←b+ηyi

(4)转至(2)，直至训练集中没有误分类点。

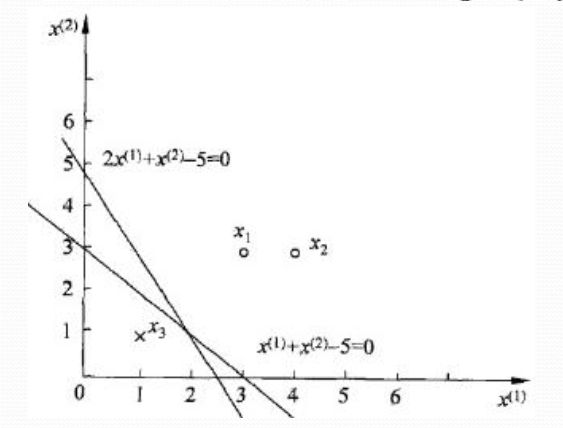
例子：如图所示，正实例点是 x1=(3,3)T,x2=(4,3)T ，负实例点是 x3=(1,1)T ，使用感知机算法求解感知机模型 f(x)=sign(w⋅x+b)

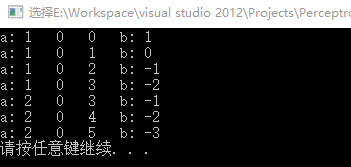
代码如下

#include "stdafx.h"
#include 

using namespace std;

const   double  lr = 1;
const   int dim = 2;
const   int n = 3;
double      w[dim] = {0, 0};
double      b = 0;
double samples[n][dim] = {3,3,      4,3,    1,1};
int labels[n] = {1, 1, -1};

//计算两个向量的内积
double dot(double *w, double *feature)
{
    double sum = 0;
    for(int i = 0; i < dim; i++)
    {
        sum += (*w) * (*feature);
        w++;
        feature++;
    }
    return sum;
}

//感知机算法
void perceptron()
{
    while(true)
    {
        int i;
        for(i = 0; i < n; i++)
        {
            if(labels[i] * (dot(w, samples[i])  + b)   <= 0)
            {
                cout << "w：(";
                for(int j = 0; j < dim; j++)
                {
                    w[j] = w[j] + lr*labels[i]*samples[i][j];
                    cout << w[j];
                    if( j != dim-1)
                        cout<<",";
                }
                b = b + lr*labels[i];
                cout << ")  b："<break;
            }
        }
        if(i == n)
            break;
    }
}

int _tmain(int argc, _TCHAR* argv[])
{
    perceptron();
    system("pause");
    return 0;
}

运行结果如下

下面来介绍感知机算法的对偶形式
对偶形式的基本思想是，将 w 和 b 表示为实例 xi 和 yi 的线性组合的形式，通过求解其系数而求得 w 和 b 。我们假设初始值 w0 和 b0 均为0，在原始形式中，对误分类点 (xi,yi) 通过

w←w+ηyixi

b←b+ηyi

逐步修改 w 和 b 。假设我们现在运行感知机算法的原始形式求得 w 和 b ，当算法结束，在样本点 (xi,yi) 处总共对 w 和 b 修改了 ni 次，则 w 和 b 关于 (xi,yi) 的增量分别是 αiyixi 和 αiyi ，这里 αi=niη 。这样最后学到的 w 和 b 可以分别表示为

w=∑i=1Nαiyixi

b=∑i=1Nαiyi

这里 αi≥0，i=1,2,3,....N ，当 η=1 时， αi 表示第 i 个实例点由于误分而进行更新的次数。

综上所述，我们可以得到感知机学习算法的对偶形式

输入：训练集 T={(x1,y1),(x2,y2),...(xN,yN)} ，其中 xi∈X=Rn ， yi∈Y={+1,−1} ， i=1,2,3,...N ；学习率 η(0<η≤1) ；
输出： α，b ；感知机模型 f(x)=sign(∑Nj=1αjyjxj⋅x+b) ,其中 α=(α1,α2,.....αN) 。
(1) α←0，b←0
(2)在训练集中选取数据 (xi,yi)
(3)如果 yi(∑Nj=1αjyjxj⋅x+b)≤0

αi←αi+η

b←b+ηyi

(4)转至(2)，直至训练集中没有误分类点。

我们依然使用上文给出的例子，利用感知机算法的对偶形式来求解，代码如下

#include "stdafx.h"
#include 

using namespace std;

// 学习率
const   double  lr = 1;
//特征维度
const   int dim = 2;
//样本个数
const   int n = 3;

//样本
double samples[n][dim] = {3,3,      4,3,    1,1};
//样本标记
int labels[n] = {1, 1, -1};
//Gram矩阵
double g[n][n];
double a[n] = {0};
double b = 0;


//计算两个向量的内积
double dot(double *w, double *feature)
{
    double sum = 0;
    for(int i = 0; i < dim; i++)
    {
        sum += (*w) * (*feature);
        w++;
        feature++;
    }
    return sum;
}

//求解Gram矩阵
void getGram()
{
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            g[i][j] = dot(samples[i],samples[j]);

        }
    }

}

double dot_antithesis(int subs)
{
    double sum = 0;
    for(int i = 0; i < n; i++)
    {
        sum += a[i]*labels[i]*g[i][subs];

    }

    return sum;

}
//感知机算法的对偶形式
void pereption_antithesis()
{
    getGram();
    while(true)
    {
        int i;
        for(i = 0; i < n; i++)
        {
            if(labels[i] * (dot_antithesis(i)  + b)   <= 0)
            {
                a[i] += lr;
                b = b + lr*labels[i];

                cout << "a: ";
                for(int j = 0; j < n; j++)
                    cout << a[j] << "   ";

                cout << "b: " << b << endl;
                break;
            }
        }
        if(i == n)
            break;
    }

}

int _tmain(int argc, _TCHAR* argv[])
{
    pereption_antithesis();
    system("pause");
    return 0;
}

程序运行结果如下