稳定排序的代码你写对了吗？

前言

所谓的稳定排序是指原来相等的两个元素前后相对位置在排序后依然不变。

未曾了解过这方面的朋友可以看一看我下面这篇文章。

几种排序算法的稳定性分析

常见的能够保证稳定性的排序算法有

• 冒泡排序
• 插入排序
• 归并排序

注意，我说的是能够保证稳定性，而非是一定稳定，这与你对算法的实现息息相关，本文就这三种可以保证稳定性的算法中较为复杂的归并排序进行举例，来阐述这篇文章的主要思想。
 

不稳定的归并排序代码实现

这里先给出一个有瑕疵的归并排序算法实现的代码，为什么说是有瑕疵而不说是错误的呢，因为这个版本是能正常排序的，但是无法保证稳定性。

而且，这个版本的代码与正确的版本仅仅差了一个符号。

下面这是一个非常常见的归并排序算法实现，我们这里使用泛型编程，方便一会儿写测试用例。

    public static <T extends Comparable<? super T>> void mergeSort(T[] arr) {
		mergeSort(arr, 0, arr.length - 1);
	}
	
	private static <T extends Comparable<? super T>> void mergeSort(T[] arr, int l, int r) {
		if (l >= r) {
			return;
		}
		int mid = l + (r - l) / 2;
		mergeSort(arr, l, mid);
		mergeSort(arr, mid + 1, r);
		//归并排序的一个简单优化
		if (arr[mid].compareTo(arr[mid + 1]) > 0) {
			merge(arr,l,mid,r);
		}
	}

	private static <T extends Comparable<? super T>> void merge(T[] arr, int l, int mid, int r) {
		T[] aux = (T[] )new Comparable[r - l + 1];
		for(int i = l;i <= r; i++) {
			aux[i - l] = arr[i];
		}
		int i = l;
		int j = mid + 1;
		int k = l;
		while(k <= r) {
			if (i > mid) {
				arr[k] = aux[j - l];
				j++;
			}else if (j > r) {
				arr[k] = aux[i - l];
				i++;
			}else if (aux[i - l].compareTo(aux[j - l]) < 0) {
				arr[k] = aux[i - l];
				i++;
			}else {
				arr[k] = aux[j - l];
				j++;
			}
			k++;
		}
		
	}

之后，我们定义一个内部类：Person ，我打算根据它的 age 来进行排序。

static class Person implements Comparable<Person>{
		int age;
		String name;
		public Person(int age,String name) {
			this.age = age;
			this.name = name;
		}
		@Override
		public int compareTo(Person other) {
			return this.age - other.age;
		}
	}

编写测试用例

public static void main(String[] args) {
		Person[] persons = new Person[4];
		persons[0] = new Person(5, "张三");
		persons[1] = new Person(5, "李四");
		persons[2] = new Person(2, "赵五");
		persons[3] = new Person(5, "王二");
		
		mergeSort(persons);
		for(Person p : persons) {
			System.out.println("姓名：" + p.name + ",年龄：" + p.age);
		}		
}

在看结果之前，我们自己先想一下，如果是稳定排序的话，结果如何？非常简单。

姓名：赵五,年龄：2
姓名：张三,年龄：5
姓名：李四,年龄：5
姓名：王二,年龄：5

年龄为 5 的这仨人应该保持跟原来一样的次序。

但是我们看一下代码执行的结果。

很抱歉，尽管确实是按照年龄排了序，但是年龄相同的人原来的顺序被打乱了。
 

问题出在哪里？

还记得我一开始说的话吗？这个版本的代码与正确的版本仅仅差了一个符号而已。

它就是 merge 函数中执行归并过程的第三个 if 分支。

aux[i - l].compareTo(aux[j - l]) < 0

我们来简单的分析一下。

看下面这个小例子，我简单的画了一个归并排序 merge 过程。

现在左右两部分都排好序了，就差 merge 了。

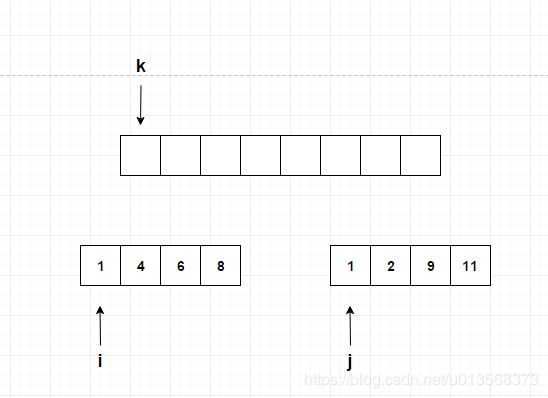
如果按照 aux[i - l].compareTo(aux[j - l]) < 0 这种比较方式的话，我们比较的就是，下标为 i 和 j 这两处值，如果 i 的值小于 j 的值，那么就把 i 的值放入 k 的位置，但是 i 的值 等于 j 的值就是问题的关键了，此时 j 的 1 会被放入 k 的位置。这就是这种实现方式不稳定的原因。

所以我们只要把这一判断表达式的运算符由 ” < “ 改成 ” <= “ 即可。

aux[i - l].compareTo(aux[j - l]) <= 0

 

说在最后

诚然，冒泡、插入、归并都是能够保证稳定性的排序算法，但是稳定性与代码的正确实现有着非常大的关系，我在网上看见非常多的归并排序的实现就是文中给出的有瑕疵的那种实现，希望看过这篇文章的读者能注意到这个细节。

另外，尽管本文拿归并排序举例，但是实际上这种思想对于冒泡、插入同样适用，在你对代码实现的时候，在比较元素大小并交换的部分一定要多留意，确保不会写出不稳定的冒泡、插入排序代码。