解密区块链中的密码学
在这片文章中,我们总结了区块链会用到的一些密码学原语,那什么是密码学“原语”?
不同于操作系统的“原语”概念,(注:操作系统原语是操作系统或计算机网络用语范畴。是由若干条指令组成的,用于完成一定功能的一个过程,具有不可分割性。)密码学原语强调的是“动机”,可以简单理解为:你想做什么事情?比如“加密”、“签名”是个原语,“密钥交换”、“零知识证明”也是个原语。
位于第一层阶层的原语可能一共有十几个左右,由第一阶层的原语派生出的,大大小小加上各种属性组合起来,可能有上千个之多。
一些密码学家,在网络上做了一个很有趣的组合,左边选原语、右边选属性,不同的原语跟不同的属性,再加上不同的公平认证框架,三者互相组合可以就产生出上千种应用,也就是新的密码原语。
而区块链是一个密码密集,比特币就是区块链的典型代表,它的基本结构可以概括成一个“双链Hash锁定”,其特性就体现在:
①它是一个全新的分布式帐本;
②它是“只增不改”;
怎么来理解这两点呢?其实杨义先原来打过一个比方的,他在《安全简史》里面把区块链比喻成一个家谱。 相当于,我说话的时候拿着一个高音喇叭在广场上面,我说出去的话被很多人听到了,当我想反悔的时候,只要有足够多的人证明你已经说过的话,你不能反悔,这样就保证你说出去的话做到只增不改。
比特币核心用密码学原语就是签名算法(ECDSA)和哈希算法(Hash)。其实区块链当中用到的密码原语有很多,比如哈希、数字签名等。而且数字签名不仅仅用了标准的数字签名,还用到了环签名、可连接环签名、一次签名,还有博罗梅环签名,以及多重签名,同态加密、同态承诺、累积器以及零知识证明等等,还有最近比较火的密码掷签。
(1)哈希函数
目前来说,我们用的哈希函数大部分三大类:SHA1、SHA2、SHA3。目前比特币里面又有一个主要是SHA0,当然现在也有一些已经用到了SHA3里面的一些。
(注::SHA即安全散列算法(Secure Hash Algorithm的缩写)是一个密码散列函数家族,是FIPS所认证的安全散列算法。SHA家族的五个算法,分别是SHA-1、SHA-224、SHA-256、SHA-384,和SHA-512,由美国国家安全局(NSA)所设计,并由美国国家标准与技术研究院(NIST)发布)
SHA3的好处是非NSA设计的,非NSA设计有一个好处,就是这里面存在着一个后门(注:后门一般是指那些绕过安全性控制而获取对程序或系统访问权的程序方法)。
从密码算法的角度来讲,如果是设计者故意藏进去的“后门”,理论上可以做到不可区分,也就是除了设计的人知道,别的人想探知“后门”的存在性,将会面对一个人非常困难的数学难题。
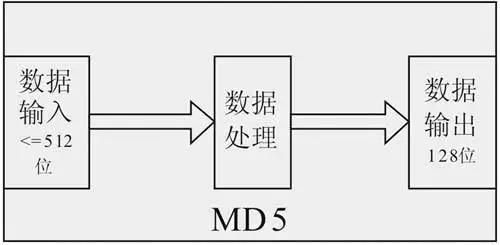
为了便于对比,我们用破解MD5做一个对比,使用不超过2的64次方的比特运算、逻辑运算就可以实现。目前行业主要使用的是SHA—256,目前上没有被破解。
注:MD5是一种被广泛使用的密码散列函数,可以产生出一个128位(16字节)的散列值(hash value),用于确保信息传输完整一致。MD5由美国密码学家罗纳德·李维斯特(Ronald Linn Rivest)设计,于1992年公开,用以取代MD4算法。
我们在提到Hash函数的时候,不可避免的要考虑一下Hash函数开放性概念,在区块链里,目前来说多数应用的是单向性。经常看有一些业界的人讲区块Hash加密的,其实Hash不叫加密,它只是取了一个摘要。
哈希函数的设计,都需要满足抗碰撞性。抗碰撞从攻击的角度要求最低,安全目标的角度很高。也就是如果攻击者连最低的攻击目标都达不到,也就意味着存在最高的安全性。还有一些典型的用于区块链其他的Hash函数,比如说Equihash、Ethash、sCrypt,sCrypt已经在推荐标准草案里面发过了。
最后总结一下“挖矿”和“对抗挖矿”,这是围绕Hash技术研究“攻”和“防”的两个概念。这是很奇异的一件事情,我们研究Hash从来没有想过把Hash的速度降低,但是区块链出来以后,使得对抗挖矿成为一个新的研究方向。
所谓对抗挖矿就是要求被计算速度不能太快,因为追求计算速度意味着不公平。比如过去的十年从最开始的一秒钟完成100兆Hash运算,到用ASIC芯片可以完成14个T。
而对抗挖矿一种是在于提高硬件内存的门槛,如Ethash、Scrypt。另一种是如X11的这种串行的设计方案。把11种Hash函数串起来调用,而X17就是17种。目的都是为了让Hash计算得慢,仍然保持着一个抗碰撞的特性。
目前为止,这么做的方法从密码学原理上面来说并没有增强安全性,Hash函数串起来用,大家或许感觉更难、更安全了,但从理论上面来说并没有。
(2)一次签名
一次签名是把签名的概念结合一次一密的思想,就是说一个签名私钥只能使用一次,如果是想使用两次就有一个危险:会泄露前面的私钥。这个概念提得很早,主要是Lamport提出的,Lamport他本人也是一个搞分布式的大家。

注:Leslie B. Lamport是美国计算机科学家。以其在分布式系统中的开创性工作以及文档准备系统LaTeX的最初开发人员而闻名。也是2013年图灵奖的获胜者,他设计了重要的算法并开发了正式的建模和验证协议,以提高真实分布式系统的质量。这些贡献提高了计算机系统的正确性,性能和可靠性
(3)环签名
关于环签名最大的特点是它的匿名性,被人描述为“拉你入环、与你何干”,也就是说我为了达到匿名性,可以随便拉一些人组成这个环,代表一个组织来发布一个消息,只要我知道这些人的公钥就可以。
打个比方,如果我们以人的名字为公钥举例子,那我可以跟特朗普的名字组合,发布一个虚假信息,然后说这个消息是特朗普发布的,而且特朗普也确实可以发布这个东西。它的匿名性都是无条件,只要你知道一个人的名字,不需要征得他的同意,就可以被你拉入到这个环当中来。
注:环签名(ring signature)是一种数字签名方案,最初由Rivest等人提出,环签名是一种简化的群签名,环签名中只有环成员没有管理者,不需要环成员间的合作。
一个好的环签名必须满足以下的安全性要求:
1)无条件匿名性。攻击者即使非法获取了所有可能签名者的私钥,他能确定出真正的签名者的概率不超过1/n,这里n 为环成员(可能签名者)的个数。
2)不可伪造性。外部攻击者在不知道任何成员私钥的情况下,即使能够从一个产生环签名的随机预言者那里得到任何消息m 的签名,他成功伪造一个合法签名的概率也是可以忽略的。
3)环签名具有良好的特性。可以实现签名者的无条件匿名;签名者可以自由指定自己的匿名范围;构成优美的环形逻辑结构;可以实现群签名的主要功能但无需可信第三方或群管理员等。
环签名是一种特殊的群签名,没有可信中心,没有群的建立过程,对于验证者来说,签名人是完全正确匿名的。环签名提供了一种匿名泄露秘密的巧妙方法。环签名的这种无条件匿名性在对信息需要长期保护的一些特殊环境中非常有用。例如,即使RSA被攻破也必须保护匿名性的场合。
(4)可连接环签名
环签名的匿名性是很好,但是这个匿名性太强悍了,以至于常常被用来洗钱、干坏事。所以人们对于环签名提出了一些限制,也就是可连接的环签名,就是环中同一个人的两次环签名可以链接,但是签名的身份仍然是你匿名的。
其实到这个层次,环签名和群签名有点类似之处了。群签名的概念是91年Chaum提出的。Chaum也是盲签名的提出者,第二次货币的研究就起源于1981年、80年左右,他在十年之后,提出了群签名的概念。
群签名是有一定的匿名性,对验证者是匿名的,但是对群管理员来说不是匿名的,能够查找出来是谁签的。

这两个概念,可连接的群签名和可连接的环签名当初都有各自的发展,而且都在区块链当中使用,最后这些技术结合在一起,实现了环签名交易,这个是门罗币隐藏交易金额的一个关键技术。
(5)博罗梅环签名
最初门罗币想用博罗梅环签名来做交易金额的范围证明,想把交易金额的范围证明想隐藏起来,后来因为博罗梅环签名的效率很低而放弃。博罗梅有一个历史来源,以前一个很古老的家族博罗梅家族,用三个环绕的环做了一个家族的徽标,数学上面抽象起来就是这样,这三个环打开其中任何一个的时候,另外两个环已经同时被打开了。
上面说过环签名是有匿名性的,把多个环签名放在一起,通过“或运算”可以把其看成每一个签名人。
比如这个签名是X1、X2签的,或者Xn签的,这一块代表真,表示这里面有一个人签了名。此外另外一个Y1签或者Y2签,也是同样的原理。每一个里面到底是谁签的,就是匿名的,匿名性是靠“或逻辑”实现的,而同时有效是靠“与逻辑”实现的。
博罗梅环签名的意思是,一个环签名具有匿名性,那么把多个环签名拼在一起,就完成了一个交易金额的证明,一旦有一个环被公开或者有一个环的匿名性丢失的时候,整个匿名性就丢失了,这是博罗梅环签名。
(6)多重签名与聚合签名
多重签名跟聚合签名的概念稍微有些不一样,比聚合签名稍微简单一些。多重签名就是对于与相同消息的多个不同的签名聚合在一起,最后验证的时候只验证一次,就是不同的人对同一个消息进行签名,在区块链当中用得比较少。

而聚合签名比多重签名这个范围更广一些,聚合签名就把这个“相同”两个字可以改成“不同”。聚合签名把不同消息的多个签名,签名人不同,签名消息也可能不同,还可以聚合成一个签名,最终签名还可以一样的。目前还没有发现区块链项目应用聚合签名,但是多重签名确实用到了。
(7)同态加密
同态加密是一直是区块链和加密货币行业讨论的焦点,大家都对这个技术很关心,但是后来发现,就目前来说,同态加密这个技术,在区块链中还用得比较浅显,用的也很少。
同态加密的概念就是无需解密,基于密文(注::密文是加了密的的文字,明文是加密之前的文字。密文是对明文进行加密后的报文)能够做一些运算,它在安全计算、云计算当中都有很广泛的应用。为了理解同态加密,我们可以从“加法同态”开始,也就是两个密文加起来再解密,相当于两个消息加在了一块。
而“乘法同态”就是两个密文乘起来(特殊的乘法)再解密。“全同态”就是同时支持一组逻辑完备操作。实际上数学已经证明,定义在任何一个环上,只有满足加法、乘法,就是最完备的,所以说只要同时实现了加法同态和乘法同态,相当于实现了全同态。
同态加密在区块链当中还没有直接使用。Zcash只有在最开始的一个构造的证明当中用了一步同态加密,而且是线性同态加密,还不是全同态加密。
(8)同态承诺
目前很多人所说的同态加密对区块链很重要,实际描述的是来同态承诺。同态承诺在区块链当中确实用得很多。承诺和加密的区别在哪?
承诺是不需要打开或者是只有出现纠纷的时候才能打开。任何一个加密方案都可以变成一个承诺方案。承诺方案比加密方案构造各个方面要简单,逻辑上要简单很多。

从密码构造、原子度构造的角度来说,承诺就是利用任何的单项函数,也就是说我只有一个Hash函数就可以构造出来。Hash函数我们通常看是非常有效的单项函数。但到目前为止,如果只靠单项函数,还无法将加密构造出来。
(9)累积器
累积器的作用,一方面是用来构造环签名,另一方面是直接在区块链当中使用,可能门罗币当中就有用了。关于累积器,国内也有翻译成聚合器的,这是一个很好的概念。
它可以把很多个对象压缩到一个空间里面,而且压缩起来的空间跟原来每个对象的空间几乎还是一样大。但是同时根据特定的条件,还会构造出“成原证据”和“非成原证据”,比如说一半就能够证明你在里面或者证明你不在里面,这就需要累积器,可以概括为八个字“万众归一、真假可辨”。
这个潜力是了不得的,在区块链当中肯定是希望使用这样的东西。比如说把很多笔交易压缩成一个交易,传输很快,而且如果真正拿出一个交易的时候,我还能够证明你在里面或者是你不在里面。
当然,这里面有一个必须消除的误解,比如我给你一个压缩后的东西,你从这个里面“抽出”那一个东西,是抽不出来的。
基于信息论上可知,信息压缩是有丢失的。比如说把一千兆的一个比特信息压成1K,肯定有信息丢失,但是我构造的巧妙,你拿了一个原模原样的东西,你问在不在我这个压缩的里面,我能证明它在里面或者证明它不在里面,这就是它的奇妙之处,而抽是抽不出来的。
打一个比方,有一个保密箱包含着每个人的半截头发,因为每个人的基因都是不同的,我可以通过半截头发,来证明你是否在这个保密箱里。但是从基因的保密箱子里面克隆出一个完整的人来则不行。
这一点对于很多应用来说这个已经很好了,目前对于聚合器在区块链里的应用,大家探索得还不够,如果能够找到直接使用的方法是最好的。
(10)零知识证明
顾名思义,零知识证明就是既能充分证明自己是某种权益的合法拥有者,又不把有关的信息泄露出去——即给外界的“知识”为“零”。其实,零知识证明早在16世纪的文艺复兴时期,意大利有两位数学家为竞争一元三次方程求根公式发现者的桂冠,就采用了零知识证明的方法。
当时,数学家塔尔塔里雅和菲奥都宣称自己掌握了这个求根公式,为了证明自己没有说谎,又不把公式的具体内容公布出来(可能在当时数学公式也是一种技术秘密),他们摆开了擂台:双方各出30个一元三次方程给对方解,谁能全部解出,就说明谁掌握了这个公式。
比赛结果显示,塔尔塔里雅解出了菲奥出的全部30个方程,而菲奥一个也解不出。于是人们相信塔尔塔里雅是一元三次方程求根公式的真正发现者,虽然当时除了塔尔塔里雅外,谁也不知道这个公式到底是个什么样子。从这个故事,我们可以初步了解零知识证明的概念。
零知识证明是由S.Goldwasser、S.Micali及C.Rackoff在20世纪80年代初提出的。它指的是证明者能够在不向验证者提供任何有用的信息的情况下,使验证者相信某个论断是正确的。
零知识证明实质上是一种涉及两方或更多方的协议,即两方或更多方完成一项任务所需采取的一系列步骤。证明者向验证者证明并使其相信自己知道或拥有某一消息,但证明过程不能向验证者泄漏任何关于被证明消息的信息。
大量事实证明,零知识证明在密码学中非常有用,如果能够将零知识证明用于验证,将可以有效解决许多问题。关于区块链,人们都还比较关心零知识证明,特别是Zcash提出了相关的技术zk—SNARK。
(注:Zcash 是首个使用零知识证明机制的区块链系统,它可提供完全的支付保密性,同时仍能够使用公有区块链来维护一个去中心化网络。与比特币相同的是,Zcash代币(ZEC)的总量也是2100万,不同之处在于,Zcash交易自动隐藏区块链上所有交易的发送者、接受者及数额。只有那些拥有查看密钥的人才能看到交易的内容。用户拥有完全的控制权,他们可自行选择向其他人提供查看密钥。)
zk—SNARK的构造形式很复杂,可以说是一个“十八般武艺”的大集成,它是基于同态加法的多项式盲计算与盲验证,然后基于这个二次算术编程的任意算术证明,然后基于椭圆曲线进行配对的一次乘法的合成。它还有引入了公共参考串,公共参考串在其中起到了随机性内嵌的一个作用,试图实现去中心化。
(11)密码掷签
密码透支的基本思想是用抽签的方式决定或者筛选出潜在的参与者,之后参与者再进行抽签,最终第i个用户是第r轮被选为潜在的leader的条件。为了满足第i个用户在第r轮第s步被选为验证者的条件。这个签名当中有历史签名存在,所以别人篡改不了这个,所以就是掷签。
相当于把历史整体可以看出来是随机串。然后通过P1、P2参数的调整,可以证明在它的当中产生分杈的概率是可以忽略的,这是一个很强悍的概念。可忽略这个概率是呈指数下降的,只要系统参数足够长。十万分之一、百万分之一、千万分之一都不叫可忽略。可忽略要比任意多项式的DOS还小,降低的速度都还要快,这叫可忽略。
延伸阅读:区块链:密码学基础