深入浅出神经网络与深度学习--神经元感知机单层神经网络介绍（-）

1     概述

写神经网络与深度学习方面的一些知识，是一直想做的事情。但本人比较懒惰，有点时间想玩点游戏呀什么的，一直拖到现在。

也由于现在已经快当爸了，心也沉了下来，才能去梳理一些东西。本文会深入检出的去看神经网络与深度学习的一些知识，包含一些算法、基础等，比较适合初学者。

文笔有限，有些不好理解的地方会配图及实例。

本文主要使用neuroph做实例进行讲解去理解机器学习相关，为什么会选用这个呢，下边也有介绍。主要如果用tenseflow与spark等，会使用其他语言，如scala、python，会有一定的学习成本。而neuroph完全是为java提供的算法库，运行环境当然是JVM。导入jar包即可运行。

本文参考不止一本教程及资料，所以有些地方显得比较杂乱，后续会持续更新，并对此做修改

2.1   神经元

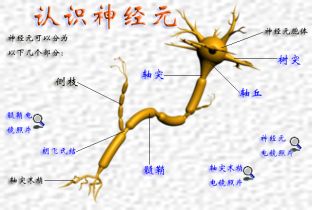
说神经网络，那么必须先看下生物神经网络的组成与行为方式。

人工神经元模拟了生物神经元的仿生工程。是模仿生物神经元组成的神经网络在接收刺激及信号传递等行为。具体可查看第二章第一节人工神经元构造。

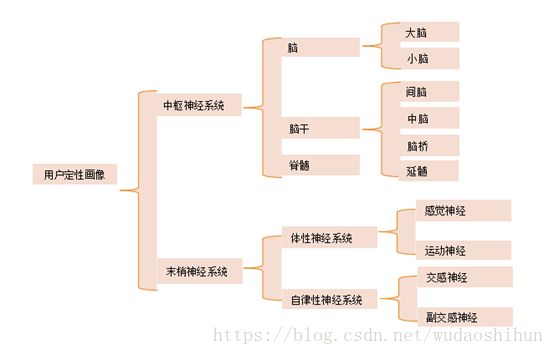
我们可把神经元归纳为：

l  感觉神经元（传入神经元）：其树突的末端分布于身体的外周部，接收来自体内外的刺激，将兴奋传至脊髓和脑。

l  运动神经元（传出神经元）：其轴突大于肌肉和腺体。

l  联络神经元（中间神经元）：结余上述2种神经元之间，起着神经元之间技能联系的作用，多存在于脑和脊髓里。

 

2.2   神经网络

2.2.1 组成

 

这里我们要说一个概念：

自组织：每个神经元都自己决定和另外哪些神经元链接，甚至不链接，没有从一个领导的角色去安排大家的工作，这种自决定的特性，构成了神经元的自主学习（对应与神经网络模型的训练）。

神经元的这种自组织特性来自于神经网络结构的可塑性，即神经元之间相互连接的突触随着动作电位脉冲激励方式与强度的变化，其传递电位的作用可增加或减少，简单的说就是输入（树突）输出（轴突）部分是可以由链接强度来表示。

 

 

3     神经网络

3.1   人工神经元构造

 

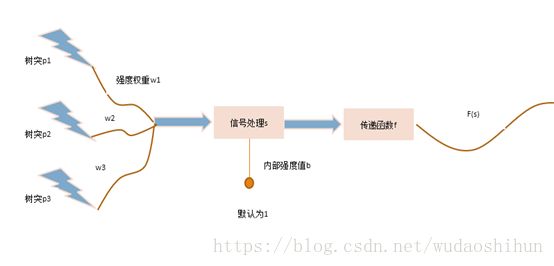
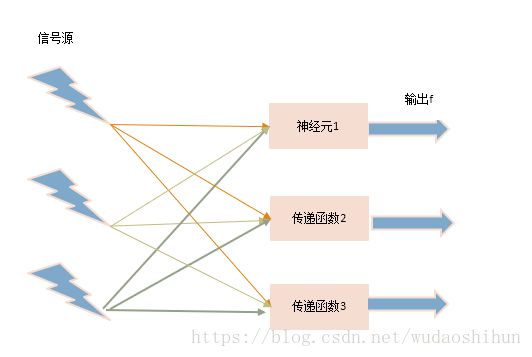
看上图，我们通过生物神经元机制知道，树突收集刺激源往后传递，刺激源是外界感知，也可以是其他神经元细胞产生的结果（output）作为神经元的输入（input）。其中w代表刺激强度。而传递函数，现阶段可简单理解为把s(n)输出结果格式化为我们想看到的符号或数字。

由生物神经元我们知道，神经元有其本身的特性，我们通过在信号处理处增加一个处理输入源b来模拟这种内部强度。

传递函数f：现阶段我们可以狭义的理解为格式化输出结果，将结果变成我们可以使用的一种符号或数字。

 

那么我们通过上述，可得到一个公式：

s = p1w1+p2w2+p3w3 + b*1

 

3.2   感知机

3.2.1 定义

网络接收若干输入，并通过输入函数、传输函数给出一个网络的输出，我们称之为感知机，即单一的最简单的神经网络。

3.2.2 解决一个简单的问题

并且，我们通过感知机的学习来解决一个实例。

品种	颜色	形状
橘子	1橙色	1圆形
香蕉	-1黄色	-1弯形

那么，如何识别香蕉和橘子呢。

通过公式：

s = p1w1+p2w2+p3w3 + b*1

预设值：b=0,w1=w2=1

 

对橘子鉴别：

s = 1*1+1*1+0 = 2

香蕉

s = -1*1+-1*1+0 = -2

通过step函数我们得到输出 1，-1分别为橘子，香蕉

但如上述，如果预设值为别的值，结果可能是不对的，那么，如何保证随意输入参数都能得到正确的结果呢。下边我们来看感知机是如何学习的

3.2.3 感知机的学习

感知机的训练方法比较简单，主要是修改神经网络的权值和偏置。

w(new) = w(old) + ep

b(new) = b(old) + e

e表示误差，e = t-a,  t为期望输出， a为实际输出

 

测试1：预设w1=1,w2=1,b=0

期望结果：1

s = p1w1+p2w2+b=0

e = t-a = 1-0 = 1

w1new = w1old + ep = 1 + 1*1 = 2

w2new = w2old +ep = -1 +1*1 = 0

bnew = bold+e = 0+1 = 1

 

net = p1w1+p2w2+b = 1*2+1*0+1=3

f(step) = 1;

 

通过有监督学习的方法来进行纠正误差。

 

3.2.4 感知机学习一个简单的逻辑运算

实现一个and运算逻辑，通过这个简单的知道他是如何运算及学习的。

 

package com.neuroph.lxl.sample;

 

import java.util.Arrays;

 

import org.neuroph.core.NeuralNetwork;

import org.neuroph.core.data.DataSet;

import org.neuroph.core.data.DataSetRow;

import org.neuroph.core.events.LearningEvent;

import org.neuroph.core.events.LearningEventListener;

import org.neuroph.core.learning.LearningRule;

import org.neuroph.core.learning.SupervisedLearning;

 

 

 

import com.neuroph.lxl.util.IterateExport;

import com.neuroph.lxl.util.Perceptron;

 

 

publicclass AndSample implements LearningEventListener{

 

    @Override

    publicvoid handleLearningEvent(LearningEvent event) {

      

       SupervisedLearningbp = (SupervisedLearning)event.getSource();

       if(event.getEventType() != LearningEvent.Type.LEARNING_STOPPED){

            System.out.println(bp.getCurrentIteration()+ ". iteration : "+ bp.getTotalNetworkError());

       }

      

    }

    publicstaticvoid and(DataSet set){

       set.addRow(new DataSetRow(newdouble[]{0,0},newdouble[]{0}));

       set.addRow(new DataSetRow(newdouble[]{0,1},newdouble[]{0}));

       set.addRow(new DataSetRow(newdouble[]{1,0},newdouble[]{0}));

       set.addRow(new DataSetRow(newdouble[]{1,1},newdouble[]{1}));

    }

   

    publicstaticvoid xor(DataSet set){

       set.addRow(new DataSetRow(newdouble[]{0,0},newdouble[]{0}));

       set.addRow(new DataSetRow(newdouble[]{0,1},newdouble[]{1}));

       set.addRow(new DataSetRow(newdouble[]{1,0},newdouble[]{1}));

       set.addRow(new DataSetRow(newdouble[]{1,1},newdouble[]{0}));

    }

    publicstaticvoid main(String[] args) {

      

       //建立训练集，有2个输入一个输出

       DataSet set = new DataSet(2,1);

      

       //and(set);

       xor(set);

      

       NeuralNetwork myp = new Perceptron(2,1);

       LearningRule lr = myp.getLearningRule();

       lr.addListener(new AndSample());

       myp.learn(set);

       IterateExport.testNeuralNetwork(myp, set);

      

    }

     

}

 

输出

package com.neuroph.lxl.util;

 

import java.util.Arrays;

 

import org.neuroph.core.NeuralNetwork;

import org.neuroph.core.data.DataSet;

import org.neuroph.core.data.DataSetRow;

 

publicclass IterateExport {

 

     publicstaticvoid testNeuralNetwork(NeuralNetworkneuralNet, DataSet testSet) {

 

            for(DataSetRow testSetRow : testSet.getRows()) {

                neuralNet.setInput(testSetRow.getInput());

                neuralNet.calculate();

                double[] networkOutput = neuralNet.getOutput();

 

                System.out.print("Input: " + Arrays.toString( testSetRow.getInput() ) );

                System.out.println(" Output: " + Arrays.toString( networkOutput) );

            }

        }

   

}

 

 

直接运行查看即可，对此不做过多的论述。

 

 

3.3   单层神经网络

又称为单层前馈神经网络。

一般情况下不会用单层神经网络解决问题。

 

 

3.4   多层神经网络

3.4.1 概述

首先了解下层的概念

l  感知器：感知器是一种双层神经网络模型，一层为输入层（输入刺激），另一层具有计算单元，可以通过监督学习建立模式判别的能力。

l  多层神经网络：也称为前馈神经网络。

       特点：前馈网络的各神经元接受前一级输入，并输出到下一级，无反馈。

       节点：输入节点，输出节点

l  计算单元：可有任意一个输入，但只有一个输出，输出可耦合到任意多个其他节点输入。

l  层：可见层-输入和输出节点；隐层-中间层。

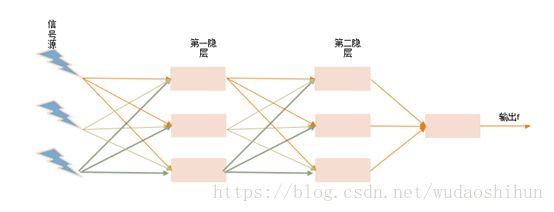
我们把中间的单层神经元扩展为2个神经元层，第一隐层，第二隐层；把由输入的信号源、隐层及输出组成的层叫做多层神经网络。

 

我们现在来看，什么情况下会用到多层神经网络，用多层神经网络能解决什么问题。

我们通过一个简单的例子来说明。

3.4.2 XOR问题

XOR运算规则：

0 xor 0 = 0

0 xor 1 = 1

1 xor 0 = 1

1 xor 1 = 0

我们通过单层神经网络，及上述的感知机去学习并运算，10W次没有得到结果…….，

什么原因导致的呢？

回到橙子与香蕉的区分问题，我们知道一点，大多数情况下，水果特征并不像上述说的那么明显，在这种情况下，我们并不能很明显的去区分特征。

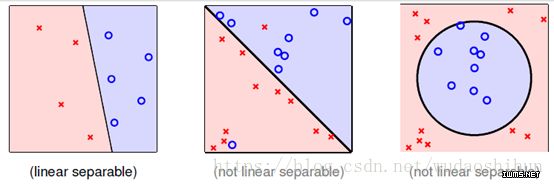
也就是不能通过一条直线，去分隔2个特征，即引入一个新概念，线性不可分。如图所示：

 

 

 

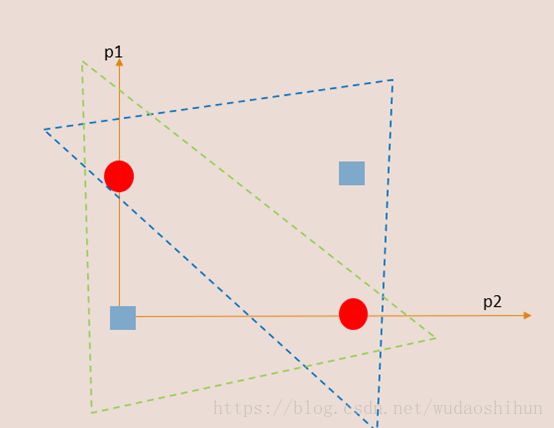
由上图我们看到XOR问题，我们具体问题具体分析，像XOR这种线性不可分问题。

使用step函数：

 

第一层上测神经元，p1,p2净输入为2p1+2p2-1,对应XOR图蓝色三角圈入

p1/p2	0	1
0	-1 = 0	1 = 1
1	1 = 1	3 = 1

 

下侧：-2p1-2p2+3，对应XOR图绿色三角圈入

p1/p2	0	1
0	3 = 1	1 = 1
1	1 = 1	-1 = 0

 

第二层神经元进行and运算。那么 第一层上测与下侧结果为第二层神经元的输入，对比2个表格的结果，计算如下：

当 p1=0,p2=0时， 0 and1 = 0

当p1=0,p2=1时，1 and 1= 1

当 p1=1,p2=0时，1 and1 = 1

当 p1=1,p2=1时，1 and0 = 0;

解决了XOR问题。

 

3.4.3 XOR代码实现

package com.neuroph.lxl.sample;

 

import org.neuroph.core.NeuralNetwork;

import org.neuroph.core.data.DataSet;

import org.neuroph.core.data.DataSetRow;

import org.neuroph.core.events.LearningEvent;

import org.neuroph.core.events.LearningEventListener;

import org.neuroph.core.learning.LearningRule;

import org.neuroph.core.learning.SupervisedLearning;

import org.neuroph.nnet.MultiLayerPerceptron;

import org.neuroph.nnet.learning.BackPropagation;

import org.neuroph.nnet.learning.MomentumBackpropagation;

import org.neuroph.nnet.learning.ResilientPropagation;

import org.neuroph.util.TransferFunctionType;

 

import com.neuroph.lxl.util.IterateExport;

 

publicclass XorSample implements LearningEventListener{

   

   

   

    @Override

    publicvoid handleLearningEvent(LearningEvent event) {

       BackPropagation bp = (BackPropagation)event.getSource();

       //SupervisedLearning bp= (SupervisedLearning) event.getSource();

       if(event.getEventType() != LearningEvent.Type.LEARNING_STOPPED){

            System.out.println(bp.getCurrentIteration()+ ". iteration : "+ bp.getTotalNetworkError());

       }

      

    }

   

   

    publicstaticvoid xor(DataSet set){

       set.addRow(new DataSetRow(newdouble[]{0,0},newdouble[]{0}));

       set.addRow(new DataSetRow(newdouble[]{0,1},newdouble[]{1}));

       set.addRow(new DataSetRow(newdouble[]{1,0},newdouble[]{1}));

       set.addRow(new DataSetRow(newdouble[]{1,1},newdouble[]{0}));

    }

    publicstaticvoid main(String[] args) {

      

       //建立训练集，有2个输入一个输出

       DataSet set = new DataSet(2,1);

       xor(set);

       //multiStudy(set);

       //设置ResilientPropagation学习规则,作废，现阶段一般用反向传播机制

       resilientStudy(set);

       

       

    }

 

 

    privatestaticvoid resilientStudy(DataSet set) {

      

       // 转移函数采用sigmoid,也可以用tanh之类的

       MultiLayerPerceptron mlp = new MultiLayerPerceptron(TransferFunctionType.SIGMOID, 2, 3, 1);

       // ResilientPropagation学习规则

        mlp.setLearningRule(new ResilientPropagation());

        LearningRule learningRule = mlp.getLearningRule();

       // 学习

       learningRule.addListener(new XorSample());

        System.out.println("Training neural network...");

        mlp.learn(set);

        intiterations = ((SupervisedLearning)mlp.getLearningRule()).getCurrentIteration();       

        System.out.println("Learned in "+iterations+" iterations");

 

        System.out.println("Testing trained neural network");

        IterateExport.testNeuralNetwork(mlp, set);

      

    }

 

    privatestaticvoid multiStudy(DataSet set) {

       // 创建多层感知机，输入层2个神经元，隐含层3个神经元，最后输出层为1个隐含神经元，

       // 使用双曲正切TANH传输函数最后格式化输出

       MultiLayerPerceptron mlp = new MultiLayerPerceptron(TransferFunctionType.TANH, 2, 2, 1);

       // 启用batch模式

       if (mlp.getLearningRule() instanceof MomentumBackpropagation)

           ((MomentumBackpropagation) mlp.getLearningRule()).setBatchMode(true);

      

       //反向误差传播 

        mlp.setLearningRule(new BackPropagation()); 

       LearningRule learningRule = mlp.getLearningRule();

       // 学习

       learningRule.addListener(new XorSample());

       mlp.learn(set);

       // 测试感知机

       IterateExport.testNeuralNetwork(mlp, set);

       // 保存结果

       mlp.save("mlp.nnet");

       NeuralNetwork loadedMlp = NeuralNetwork.load("mlp.nnet");

       // test loaded neural network

       System.out.println("Testingloaded neural network");

       IterateExport.testNeuralNetwork(loadedMlp, set);

 

    }

 

}