神经网络一之神经网络结构与原理以及python实战

鄙人的新书《elasticsearch7完全开发指南》，欢迎订阅！

https://wenku.baidu.com/view/8ff2ce94591b6bd97f192279168884868762b8e7

《kibana权威指南》

https://wenku.baidu.com/view/24cfee1ce43a580216fc700abb68a98270feac21

视频教学地址：https://edu.csdn.net/course/detail/8574

技术交流qq群： 659201069

本系列埔文由浅入深介绍神经网络相关知识，然后深入神经网络核心原理与技术，最后浅出python神经网络编程实战。通过本系列博文，您将彻底理解神经网络的原理以及如何通过python开发可用于生产环境的程序。本博文论讨神经网络的结构与原理

计算机所长：

了解计算机源理的人都知道计算机只适合做与之相匹配的任务（计算机只能执行0和１的二制机加法），如数学计算、绘制图表，目前的计算机每秒可以执行１０数量级的加法运算，但是计算机也有软肋，下面几张简单的数字图片，人类很容易识别，但计算机却很难识别出来。
　　　

人类所长：

对于上面几副图片，我们快速准确的识别出图片上的内容。我们人类可以识别复杂图片上的大量信息，但计算机却很难做到。

人工智能：

每秒几十亿次计算能力的计算机却识别不出图片中的几个数字，这是因为人类具有思维能力。但时人们想利用计算机的快速运算、进行图片识别之类的功能，这就是人工智能要解决的问题。

人类思维过程：
　　

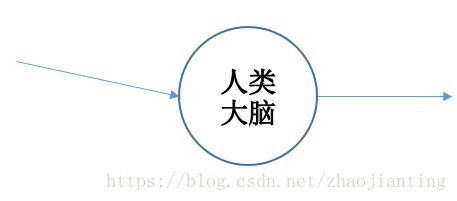
　　我们从眼睛输入图片、耳朵输入音乐，经过大脑分析，最后给出答案

计算机模仿人类思维过程：

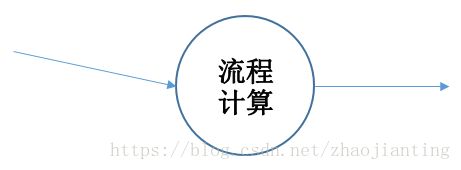
　　计算机只能拿到图片的像素，也就是只能拿到一系列的0和1的数组，而且计算机不能思考只能执行程序员预先设定好的流程，最后给出答案，本文要讨论的就是上图计算机的“流程计算”如何实现人类的智能。

神经元：
　　
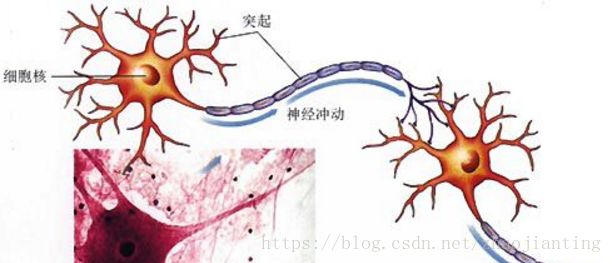
　　神经元接受电信号，从一个神经元传到别一个神经元，这就是身体感知光、声、电、热等信号的机制。电信号最到传到大脑，而大脑本身也就由神经元组成的。神经元接受大信号后不会立即反应而是抑制输放，直接信号强度达到一个预阈值，才会产生输出（后面的没激活函数就是模仿神经元的这个功能）。

计算机的神经元实现：

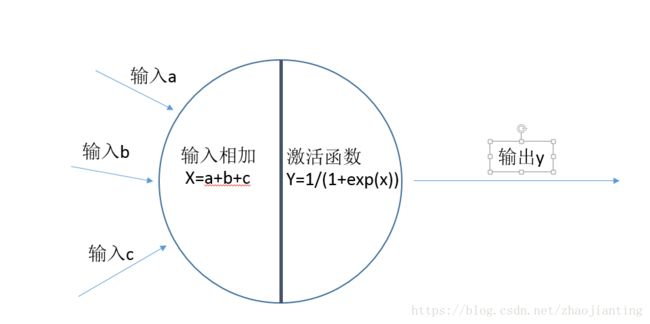
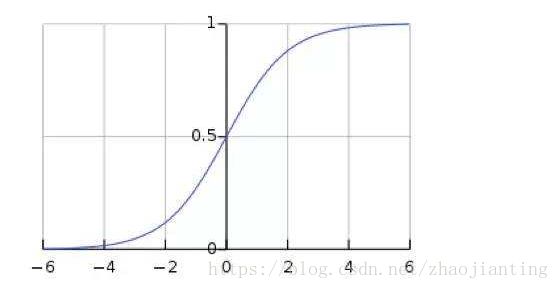
神经元可以接受多个输入，然后对它们相加，作为激活函数的输入，激活函数最后给出输出。这就是神经网络的核心神经元的主要原理。激活函数现在有好多个，我们采用S函数（后面的博文再专门讨论激活函数），图像如下：
　　

神经网络结构与原理
　　
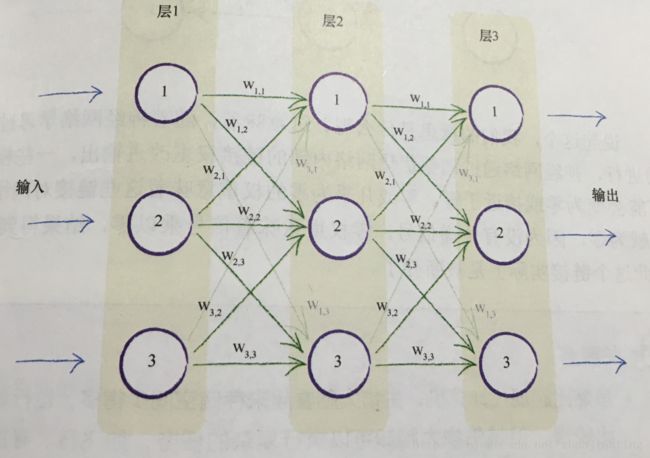
　　神经网络就是由分成多层的多个神经元组成（现在的神经网络可以达到百层以上）。每个层中的每个神经元都与其前后层的神经元互连，这种网络结构称全连接神经网络，这是经典的神经网络也就应用最多的神经网络。当然后面又了出现了卷积神经网络，在此不做讨论。

上面的神经网络分三层，分层由三个神经元，每个神经元的间的连接都有都有一个权重，较大的权重给加经输入，较小的会弱化输入。
　看下图展示了输入信号在神经网络的整个传输过程
　
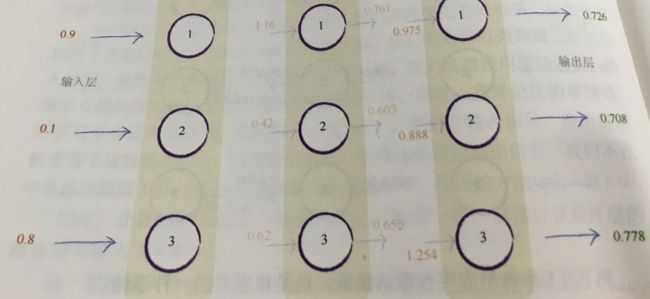
　输入为
　
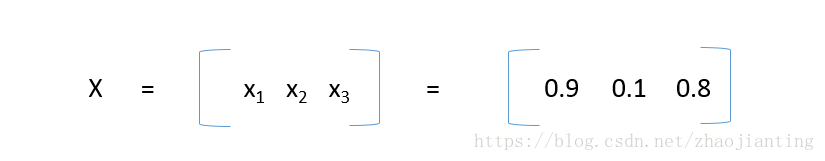
也就是第一层第一个节点输放为0.9，第一层第二个节点输放为0.1，第一层第三个节点输放为0.8

第一层和第二层的连接权重为，也就是第一层第一个节点和第二层第二个节点连连权重为0.9，其它类似，这样表示是了为后面应用距阵进行计算

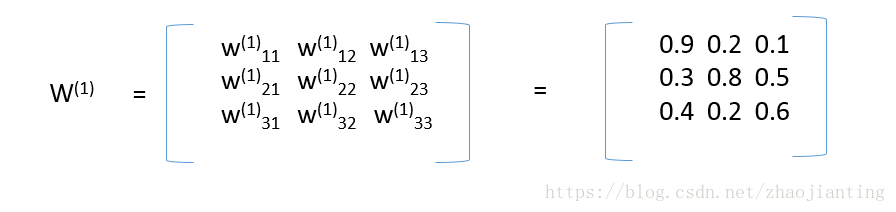
　第二层和第三层的连接权重为：

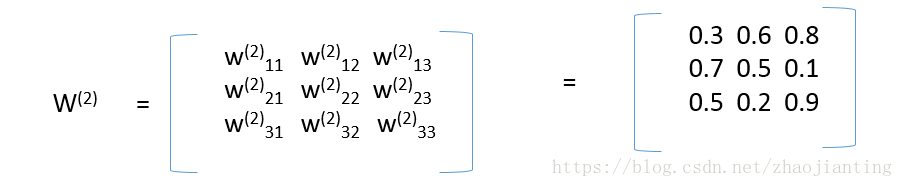
最后的出为

下面我们来分析下0.726是怎么计算出来的。下面再看下带权重的神经元结构：

输入Ｉ经过第一层直接输出原始的输入。所以第二层节点１的输入为I = [
0.9
0.1
0.8
]
这是a=0.9,b=0.1,c=0.8,Wa=0.9,Wb=0.3,Wc=0.4,也就是x=0.90.9+0.10.3+0.8*0.4=1.16,然后应用激活函数Ｓ，即y=S(X)=1/(1+exp(-1.16)) = 0.761,同理可计算第二层其它两个节点的输出，最为第二层的输放为：OH=[

第三层的输放计算方法和上面第二层的是一样的。下面看下应用矩阵的计算公式，我们分析下隐藏层和输出层各们结果的计算结果正好符合下面的矩阵乘法公式（真是无巧不成书，科学就是在巧合中一步步前进），矩阵乘法完成后，然后对每一个元素应用激活函数即可

第三层的输出也是同样的道理，第三输的输入为隐藏层的输出，矩阵乘法完成后，再对每一个元素应用激活函数即可

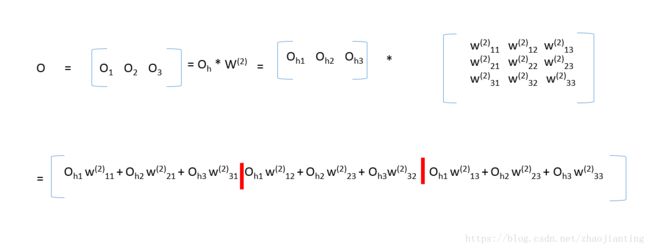
第一层称为输放层，最后一层称为输出层，中间层统称为隐藏层，无论神经网络有多少层，计算方法和上面介绍的是一样的。一开始随机得到w权重矩阵，最后根据样本一步步优化w权重矩阵。

下面是python实现的上面所讨论的三层神经网络结构：

import numpy

# python中sigmoid函数是 scipy.special.expit
import scipy.special


#三层神经网络结构定义
class neuralNetwork:

    # 初始化函数，
    #inputnodes输入层节点数目
    #hiddennodes隐藏层节点数目
    #outputnodes输出层节点数目
    #learningrate学习率，在训练时会用到，关于学习率的设置后面的文章再讨论
    
    def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
        self.inodes = inputnodes
        self.hnodes = hiddennodes
        self.onodes = outputnodes


        # wih代表输入层和隐藏层间的连接矩阵
        # who代表隐藏层和输出层间的连接矩阵
        #权重矩阵一般随机得到，但不要初始化为0和相同的值，具体的初始化方法后面会讨论
        self.wih = numpy.random.normal(0.0, pow(self.inodes, -0.5), (self.hnodes, self.inodes))
        self.who = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.onodes, self.hnodes))

        self.lr = learningrate

        # 激活函数y=1/(1+exp(-x))
        self.activation_function = lambda x: scipy.special.expit(x)

        pass


    # 查询函数，也就是由输入给出输出
    #input_list是输入层的矩阵，注意格式和维度要正确
    def query(self, inputs):
        # 输入有


        #下面两行是计算隐藏层的输出
        hidden_inputs = numpy.dot(inputs, self.wih)
        hidden_outputs = self.activation_function(hidden_inputs)

        #下面两行是计算最后的输出
        final_inputs = numpy.dot(hidden_outputs, self.who)
        final_outputs = self.activation_function(final_inputs)

        return final_outputs