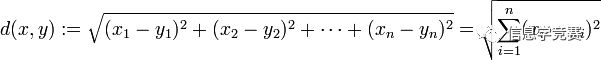KD树
目录
构造BST:
Kd-tree的构造是在BST的基础上升级:
Kd-Tree和BST的区别:
分割的概念
1.树的建立;
2.最近邻域搜索(Nearest-Neighbor Search)。
本文讲解旨在讲解Kd-Tree(K-demension tree)的一些粗浅的原理,以及其在计算机视觉的一些应用,既是总结了自己,也是分享给大家,希望有所帮助。
Kd-Tree是从BST(Binary search tree)发展而来,是一种高维索引树形数据结构,常用于大规模高维数据密集的查找比对的使用场景中,主要是最近邻查找(Nearest Neighbor)以及近似最近邻查找(Approximate Nearest Neighbor)。在计算机视觉(CV)中主要是图像检索和识别中的高维特征向量的查找和比对。
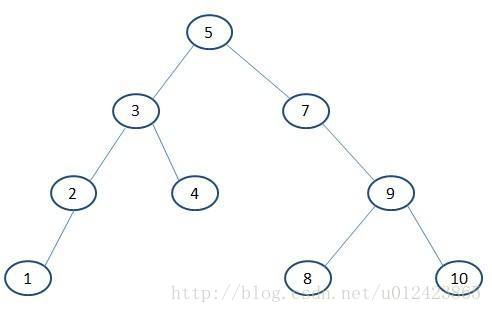
在介绍Kd-Tree之前,首先介绍下它的父系结构——BST。二叉查找树,是一种具有如下性质的二叉树:
若它的左子树不为空,则它的左子树节点上的值皆小于它的根节点。
若它的右子树不为空,则它的右子树节点上的值皆大于它的根节点。
它的左右子树也分别是二叉查找树。
构造BST:
在现有的数据中选定一个数据作为根节点的存储数值。(要求尽可能保证左右子树的集合的数量相等,优化查找速度)
将其它数据按照左小右大的规则往深层递归,直到叶节点,然后开辟新的叶节点,并存储当前值。
新的数据按照上一条进行存储。
以下就是一种二叉查找树结构示例:
如果是一维数据,我们可以用二叉查找树来进行存储,但是如果是多维的数据,用传统的二叉查找树就不能够满足我们的要求了,因此后来才发展出了满足多维数据的Kd-Tree数据结构。
Kd-tree的构造是在BST的基础上升级:
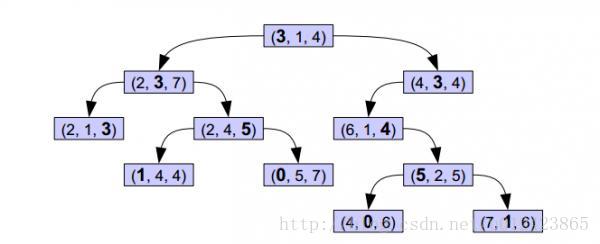
选定数据X1的Y1维数值a1做为根节点比对值,对所有的数值在Y1维进行一层BST排列。相当于根据Y1维数值a1对数据集进行分割。
选定数据X2的Y2维数值a2做为根节点比对值,对所有的数值在Y2维进行一层BST排列。也即将数据集在Y2维上又做了一层BST。
下图是一个简单的示例:
那么问题是:
如何决定每次根据哪个维度对子空间进行划分呢?
如何选定根节点的比对数值呢?
第一个问题:
直观的来看,我们一般会选择轮流来。先根据第一维,然后是第二维,然后第三……,那么到底轮流来行不行呢,这就要回到最开始我们为什么要研究选择哪一维进行划分的问题。我们研究Kd-Tree是为了优化在一堆数据中高频查找的速度,用树的形式,也是为了尽快的缩小检索范围,所以这个“比对维”就很关键,通常来说,更为分散的维度,我们就更容易的将其分开,是以这里我们通过求方差,用方差最大的维度来进行划分——这也就是最大方差法(max invarince)。
第二个问题:
选择何值未比对值,目的也是为了要加快检索速度。一般来说我们在构造一个二叉树的时候,当然是希望它是一棵尽量平衡的树,即左右子树中的结点个数相差不大。所以这里用当前维度的中值是比较合理的。
Kd-Tree和BST的区别:
BST的每个节点存储的是值,而Kd-Tree的根节点和中间节点存储的是对某个维度的划分信息,只有叶节点里才是存储的值。
在计算机视觉领域应用Kd-Tree较多的是在特征点匹配的时候,例如SIFT特征点匹配的时候,需要两两比对特征描述子的128位特征描述向量,选取汉明距离最小的做为最佳匹配点,这个时候因为要将多个特征描述向量进行大量的查找比对,Kd-Tree就能够发挥它的大作用了。当然Kd-Tree的相关知识还有最近邻查找以及怎样在回溯查找的时间复杂度和查找准确度中取舍等等,留待以后再记录。
---------------------
分割的概念
看了上面的例子,确实比较简单,但不知道为何要这样做,这里从几何意义出发,引出分割的概念。
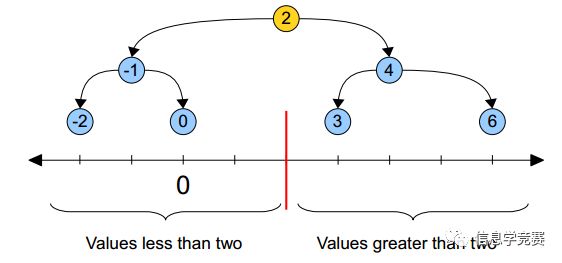
先看一个标准的BSTree,每个节点只有一个key值。
将key值对应到一维的坐标轴上。
根节点对应的就是2,左子树都在2的左边,右子树都在2的右边,整个一维空间就被根节点分割成了两个部分,当要查找结点0的时候,由于是在2的左边,所以可以放心的只搜索左子树的部分。整个搜索的过程可以看成不断分割搜索区间的过程,直到找到目标节点。
这样的分割可以扩展到二维甚至更多维的情况。
但是问题来了,二维的节点怎么比较大小?
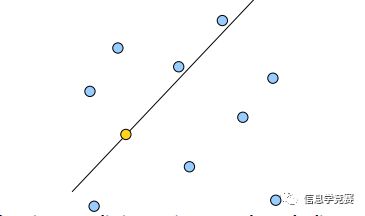
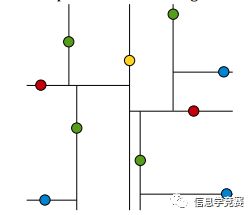
在BSTree中,节点分割的是一维数轴,那么在二维中,就应当是分割平面了,就像这样:
黄色的点作为根节点,上面的点归左子树,下面的点归右子树,接下来再不断地划分,最后得到一棵树就是赫赫有名的BSPTree(binary space partitioning tree). 分割的那条线叫做分割超平面(splitting hyperplane),在一维中是一个点,二维中是线,三维的是面。
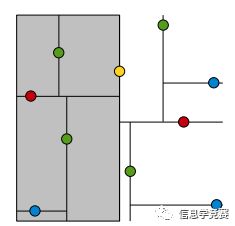
KDTree就是超平面都垂直于轴的BSPTree。同样的数据集,用KDTree划分之后就是这样:
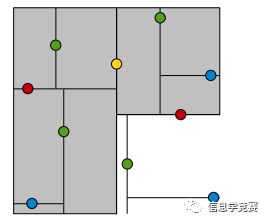
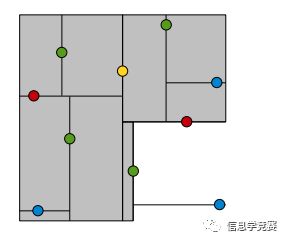
黄色节点就是Root节点,下一层是红色,再下一层是绿色,再下一层是蓝色。为了更好的理解KDTree的分割,我们在图形中来形象地看一下搜索的过程,假设现在需要搜寻右下角的一个点,首先要做的就是比较这个点的x坐标和root点的x坐标值,由于x坐标值大于root节点的x坐标,所以只需要在右边搜寻,接下来,要比较该节点和右边红色节点y值得大小...后面依此类推。整个过程如下图:
->
->
理解完KDTree之后,下面要说的就是关于KDTree的两个最重要的问题:
1.树的建立;
2.最近邻域搜索(Nearest-Neighbor Search)。
树的建立
先定义一下节点的数据结构。每个节点应当有下面几个域:
Node-data - 数据矢量, 数据集中某个数据点,是n维矢量(这里也就是k维)
Range - 空间矢量, 该节点所代表的空间范围
split - 整数, 垂直于分割超平面的方向轴序号
Left - k-d树, 由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
Right - k-d树, 由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
parent - k-d树, 父节点
建立树最大的问题在于轴点(pivot)的选择,选择好轴点之后,树的建立就和BSTree差不多了。
建树必须遵循两个准则:
1.建立的树应当尽量平衡,树越平衡代表着分割得越平均,搜索的时间也就是越少。
2.最大化邻域搜索的剪枝机会。
第一种选取轴点的策略是median of the most spread dimension pivoting strategy,对于所有描述子数据(特征矢量),统计他们在每个维度上的数据方差,挑选出方差中最大值,对应的维就是split域的值。数据方差大说明沿该坐标轴方向上数据点分散的比较开。这个方向上,进行数据分割可以获得最好的平衡。数据点集Data-Set按照第split维的值排序,位于正中间的那个数据点 被选为轴点。
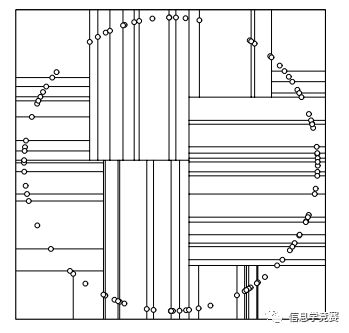
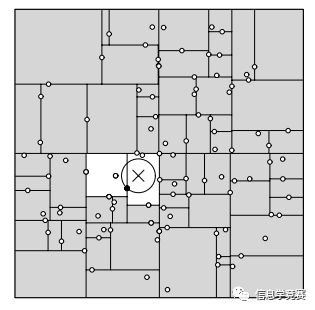
但是问题来了,理论上空间均匀分布的点,在一个方向上分割只有,通过计算方差,下一次分割就不会出现在这个方向上了,但是一些特殊的情况中,还是会出现问题,比如
这样就会出现很多长条的分割,对于KDTree来说是很不利的。
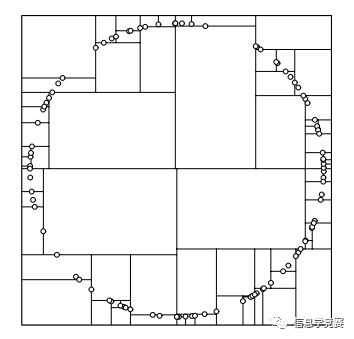
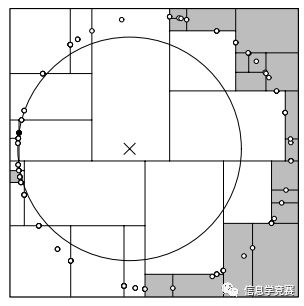
为了避免这种情况,需要修改一下算法,纬度的选择的依据为数据范围最大的那一维作为分割纬度,之后也是选中这个纬度的中间节点作为轴点,然后进行分割,分割出来的结果是:
这样的结果对于最邻近搜索是非常友好的。
但是这样做还是有一些不好,就是在树上很可能有一些空的节点,当要限制树的高度的时候,这种方法就不合适了。
邻近搜索
给定一个KDTree和一个节点,求KDTree中离这个节点最近的节点.(这个节点就是最临近点)
这里距离的求法用的是欧式距离。
基本的思路很简单:首先通过二叉树搜索(比较待查询节点和分裂节点的分裂维的值,小于等于就进入左子树分支,等于就进入右子树分支直到叶子结点),顺着“搜索路径”很快能找到最近邻的近似点,也就是与待查询点处于同一个子空间的叶子结点;然后再回溯搜索路径,并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点,如果有可能,则需要跳到其他子结点空间中去搜索(将其他子结点加入到搜索路径)。重复这个过程直到搜索路径为空。
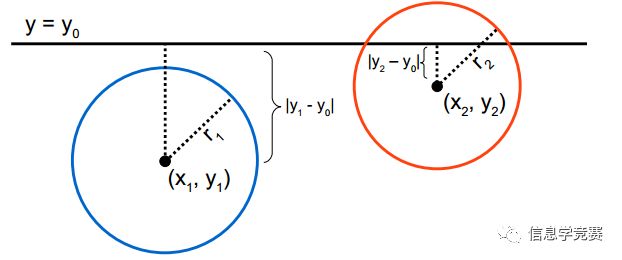
这里还有几个细节需要注意一下,如下图,假设标记为星星的点是 test point, 绿色的点是找到的近似点,在回溯过程中,需要用到一个队列,存储需要回溯的点,在判断其他子节点空间中是否有可能有距离查询点更近的数据点时,做法是以查询点为圆心,以当前的最近距离为半径画圆,这个圆称为候选超球(candidate hypersphere),如果圆与回溯点的轴相交,则需要将轴另一边的节点都放到回溯队列里面来。
判断轴是否与候选超球相交的方法可以参考下图:
下面再用一个例子来具体说一下查询的过程。
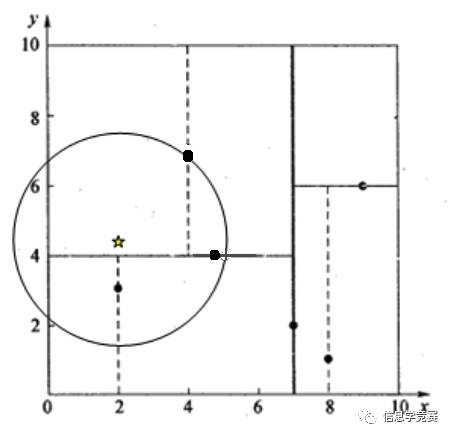
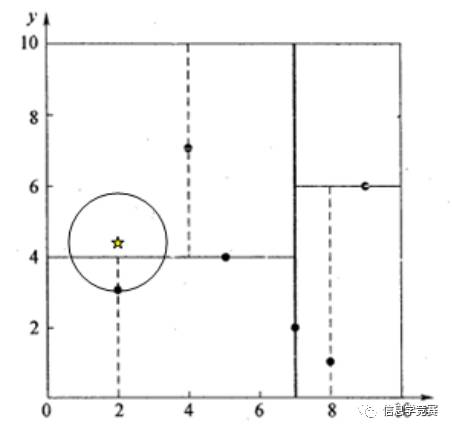
假设我们的k-d tree就是上面通过样本集{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}创建的。
我们来查找点(2.1,3.1),在(7,2)点测试到达(5,4),在(5,4)点测试到达(2,3),然后search_path中的结点为<(7,2), (5,4), (2,3)>,从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141;
然后回溯至(5,4),以(2.1,3.1)为圆心,以dist=0.141为半径画一个圆,并不和超平面y=4相交,如下图,所以不必跳到结点(5,4)的右子空间去搜索,因为右子空间中不可能有更近样本点了。
于是在回溯至(7,2),同理,以(2.1,3.1)为圆心,以dist=0.141为半径画一个圆并不和超平面x=7相交,所以也不用跳到结点(7,2)的右子空间去搜索。
至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2.1,3.1)的最近邻点,最近距离为0.141。
再举一个稍微复杂的例子,我们来查找点(2,4.5),在(7,2)处测试到达(5,4),在(5,4)处测试到达(4,7),然后search_path中的结点为<(7,2), (5,4), (4,7)>,从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202;
然后回溯至(5,4),以(2,4.5)为圆心,以dist=3.202为半径画一个圆与超平面y=4相交,如下图,所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中,现在search_path中的结点为<(7,2), (2, 3)>;另外,(5,4)与(2,4.5)的距离为3.04 < dist = 3.202,所以将(5,4)赋给nearest,并且dist=3.04。
回溯至(2,3),(2,3)是叶子节点,直接平判断(2,3)是否离(2,4.5)更近,计算得到距离为1.5,所以nearest更新为(2,3),dist更新为(1.5)
回溯至(7,2),同理,以(2,4.5)为圆心,以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。
至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2,4.5)的最近邻点,最近距离为1.5。
所以在搜索中可能会出现不同的情况,比如下面的两张图就是比较极端的两个例子。